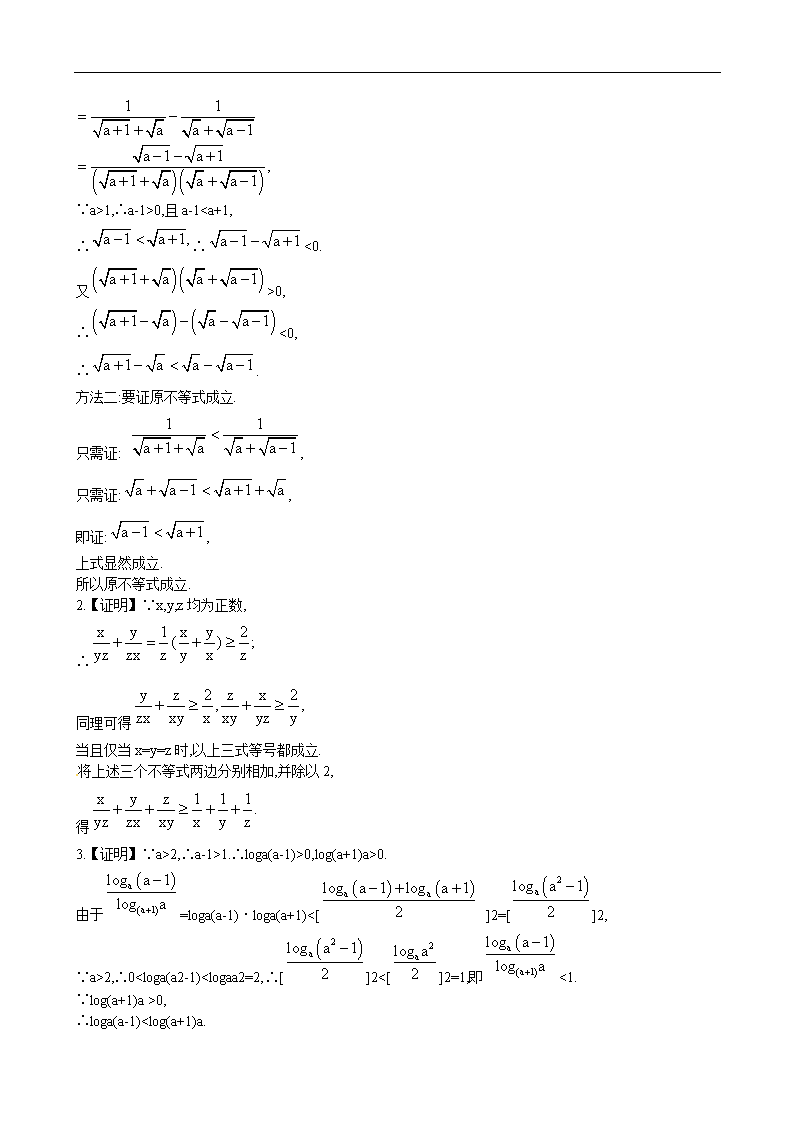高中数学 第二节 证明不等式的基本方法、数学归纳法证明不等式课时提升作业 新人教A版选修4-5
【全程复习方略】(福建专用)2014版高中数学 第二节 证明不等式的基本方法、数学归纳法证明不等式课时提升作业 新人教A版选修4-5
1.已知a>1,求证:
2.已知x,y,z均为正数,求证:
3.已知a>2,求证:loga(a-1)< log(a+1)a.
4.(2012·湖北高考)(1)已知函数f(x)=rx-xr+(1-r)(x>0),其中r为有理数,且0
0,求证:3a3+2b3≥3a2b+2ab2.
6.已知a,b,c>0,且互不相等,abc=1,证明
7.已知a>b>0,求证:
8.(2013·无锡模拟)设a,b,c是不全相等的正实数.
求证:
9.已知a,b,c∈R,f(x)=ax2+bx+c.若a+c=0,f(x)在[-1,1]上最大值为2,最小值为-,
求证:a≠0且||<2.
10.(2012·洛阳模拟)已知数列{an},{bn}满足a1=2,an-1=an(an+1-1),bn=an-1,数列{bn}的前n项和为Sn.
(1)求数列{bn}的通项公式.
(2)设Tn=S2n-Sn,求证:Tn+1>Tn.
答案解析
1.【证明】方法一:∵
∵a>1,∴a-1>0,且a-10,
∴<0,
∴.
方法二:要证原不等式成立.
只需证: ,
只需证:,
即证:,
上式显然成立.
所以原不等式成立.
2.【证明】∵x,y,z均为正数,
∴
同理可得
当且仅当x=y=z时,以上三式等号都成立.
将上述三个不等式两边分别相加,并除以2,
得
3.【证明】∵a>2,∴a-1>1.∴loga(a-1)>0,log(a+1)a>0.
由于=loga(a-1)·loga(a+1)<[ ]2=[]2,
∵a>2,∴00,
∴loga(a-1)1时,f′(x)>0,所以f(x)在(1,+∞)内是增函数.
故函数f(x)在x=1处取得最小值f(1)=0.
(2)由(1)知,当x∈(0,+∞)时,有f(x)≥f(1)=0,即xr≤rx+(1-r). ①
若a1,a2中至少有一个为0,则≤a1b1+a2b2成立;
若a1,a2均不为0,又b1+b2=1,可得b2=1-b1,于是
在①中令x=,r=b1,可得≤b1·+(1-b1),
即≤a1b1+a2(1-b1),亦即≤a1b1+a2b2.
综上,对a1≥0,a2≥0,b1,b2为正有理数且b1+b2=1,总有≤a1b1+a2b2. ②
(3)(2)中命题的推广形式为:
设a1,a2,…,an为非负实数,b1,b2,…,bn为正有理数.
若b1+b2+…+bn=1,则…≤a1b1+a2b2+…+anbn. ③
用数学归纳法证明如下:
(ⅰ)当n=1时,b1=1,有a1≤a1,③成立.
(ⅱ)假设当n=k时,③成立,即若a1,a2,…,ak为非负实数,b1,b2,…,bk为正有理数,
且b1+b2+…+bk=1,则…≤a1b1+a2b2+…+akbk.
当n=k+1时,已知a1,a2,…,ak,ak+1为非负实数,b1,b2,…,bk,bk+1为正有理数,
且b1+b2+…+bk+bk+1=1,此时00,
于是…=(…)·
=
因由归纳假设可得≤a1·
+a2·+…+ak·=,
从而…≤
又因(1-bk+1)+bk+1=1,由②得
≤·(1-bk+1)+ak+1bk+1,
从而…
≤a1b1+a2b2+…+akbk+ak+1bk+1.
故当n=k+1时,③成立,
由(ⅰ)(ⅱ)可知,对一切正整数n,所推广的命题成立.
说明:(3)中如果推广中指出③式对n≥2成立,则后续证明中不需讨论n=1的情况.
5.【证明】3a3+2b3-(3a2b+2ab2)=3a2(a-b)+2b2(b-a)=(3a2-2b2)(a-b).
因为a≥b>0,故a-b≥0,3a2-2b2>2a2-2b2=2(a+b)(a-b)≥0,
所以(3a2-2b2)(a-b)≥0,即3a3+2b3≥3a2b+2ab2.
6.【证明】方法一:∵a,b,c>0,且互不相等,abc=1.
∴
即
方法二:∵
以上三式相加,得
又∵a,b,c互不相等,∴等号不成立,
即
7.【证明】要证原不等式组成立,
只需证b>0,∴<1<成立.
∴原不等式组成立.
8.【证明】方法一:要证: >lga+lgb+lgc,
只需证:lg()>lg(abc),
只需证:>abc.
∵
∴≥abc>0成立.
∵a,b,c为不全相等的正数,∴上式中等号不成立.
∴原不等式成立.
方法二:∵a,b,c∈{正实数},
∴
又∵a,b,c为不全相等的实数,
∴>abc,
∴lg()>lg(abc),
即>lga+lgb+lgc.
9.【证明】由a+c=0得c=-a,∴f(x)=ax2+bx-a.
假设a=0或||≥2.
(1)由a=0,得f(x)=bx,依题意知b≠0,又f(x)在[-1,1]上是单调函数,
∴f(x)的最大值为|b|,最小值为-|b|.
于是|b|=2,-|b|=-,显然矛盾,故a≠0.
(2)由||≥2,得|-|≥1且a≠0,
因f(x)在[-1,1]上单调,故其最大值为|b|,最小值为-|b|,
由(1)知这是不可能的,所以||≥2不成立.
综合(1)(2)可知,假设不成立,故a≠0且||<2.
10.【解析】(1)由bn=an-1得an=bn+1代入an-1
=an(an+1-1)得bn=(bn+1)bn+1
整理得bn-bn+1=bnbn+1,
∵bn≠0,否则an=1,与a1=2矛盾,
从而得
∵b1=a1-1=1,
∴数列{}是首项为1,公差为1的等差数列.
∴=n,即bn=.
(2)∵Sn=1+++…+
∴Tn=S2n-Sn=1+++…+++…+-(1+++…+)
=++…+.
方法一:∵Tn+1-Tn=++…+
∴Tn+1>Tn.
方法二:∵Tn+1-Tn=
∵2n+1<2n+2,∴
∴Tn+1-Tn>=0.
∴Tn+1>Tn.