数学理卷·2018届广东省汕头市金山中学高三上学期期末考试+（2018

数学理卷·2018届广东省汕头市金山中学高三上学期期末考试+（2018

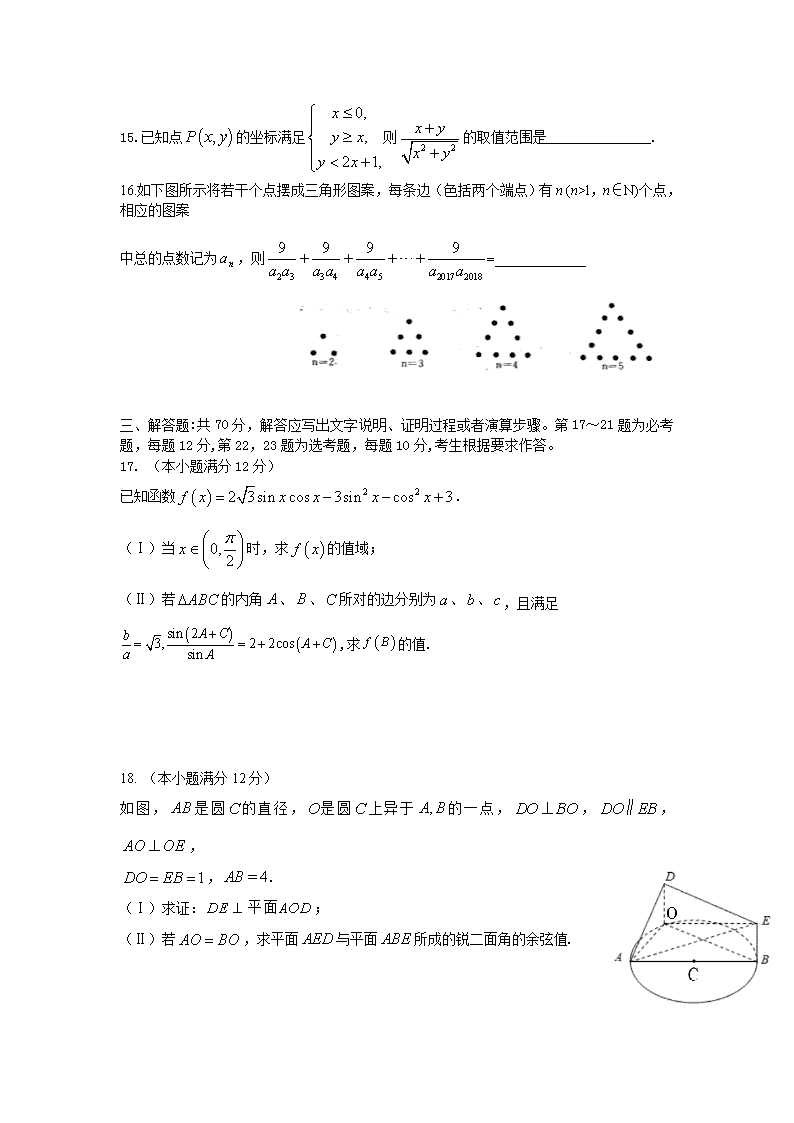
汕头市金山中学 2018 届高三理科数学期末考试试题 命题人：邓建斌 黄旭亮 一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符 合题目要求的. 1.已知集合 ， ，全集 ，则 ( ) A． B． C． D． 2.复数 , 是虚数单位, 是 的共轭复数,则下列判断正确的是( ) A. 是纯虚数 B. C. 的虚部为 D. 若 则 3.下列叙述中正确的是(　 ) A．若 a，b，G∈R，则“G 是 a，b 的等比中项”的充要条件是“G2=ab” B．在△ABC 中，若 则△ABC 为钝角三角形 C．命题“对任意 x∈R，有 x2≥0”的否定是“存在 x∈R，有 x2≥0” D．若 a，b 是异面直线，直线 c 平行于直线 a，则 c 与 b 不可能是平行直线 4．设 , 是两个非零向量．则下列命题为真命题的是（ ） A．若 ，则 B．若 ，则存在实数 λ，使得 C．若 ，则 D．若存在实数 λ，使得 ，则 5.已知向量 ＝(3，－2)， ＝(x，y－1)，且 ∥ ，若 x，y 均为正数，则3 x＋2 y的最小值是 (　　) A.5 3 B.8 3 C．8 D．24 6. 已知函数 f(x)＝cosxsin2x，下列结论中错误的是(　　) A．y＝f(x)的图像关于点(π，0)中心对称 B．y＝f(x)的图像关于直线 x＝π 2对称 C．f(x)既是奇函数，又是周期函数 D．f(x)的最大值为 3 2 7.如图所示是一个几何体的三视图，正视图是一等腰直角三角形， 且斜边 BD=2，侧视图是一直角三角形，俯视图是一直角梯形，且 AB=BC=1， 则异面直线 PB 与 CD 所成角的正切值是（ ） A．1 B． C． D． 8.在等比数列{an}中，an>0(n∈N)，公比 q∈(0,1)，且 a1a5＋2a3a5＋a2a8＝25，又 a3 与 a5 的 等比中项为 2， { | ln(1 2 )}A x y x= = − 2{ | }B x x x= ≤ U A B=  ( )UC A B = ( ,0)−∞ 1( ,1]2 − 1( ,0) [ ,1]2 −∞  1( ,0]2 − biaz += ( )Rba ∈, i z z zz + 02 ≥z z bi− ,12 −=z iz ±= 0,AB BC⋅ <  a b | |=| | | |a b a b+ −   a b⊥  | |=| | | |a b a b+ −   a bλ=  a b⊥  | |=| | | |a b a b+ −   a bλ=  | |=| | | |a b a b+ −   a b a b 2 2 2 1 2 ，数列{bn}的前 n 项和为 Sn，则当S1 1 ＋S2 2 ＋…＋Sn n 最大时，n 的值等于(　　) A.8 B.9 C.8 或 9 D. 17 9. 函数 ，若存在 ，使得 则 k 的取值范围是( ) A. B. C. D. 10.已知 ，则 （ ） A. B. C. D. 11．已知数列 各项为正数， ，△ABC 所在平面上的点 均满足△ 与△ 的面积比为 ，若 则 的值是（ ） A.1023 B.1024 C.2048 D. 2049 12. 定义在 上的函数 满足 , ，其中 是 函数 的导函数，若对任意正数 ， 都有 ，则 的取值范 围是（ ） A ． （ ） B ． （ ） C ． （ ） D ． （ ） 二、填空题:本题共 4 小题,每小题 5 分，共 20 分. 13. 已知 y＝f(x)＋x2 是奇函数，且 f(1)＝1.若 g(x)＝f(x)＋2，则 g(－1)＝________. 14. 若 两 个 向 量 与 的 夹 角 为 ， 则 称 向 量 “ ” 为 “ 向 量 积 ”，其 长 度 . 已知 ， ，则 ＝________. θ 2logn nb a= ( )f x x x= [ )1,x∈ +∞ ( )2 0,f x k k− − < ( )2,+∞ ( )1,+∞ 1 ,2  +∞   1 ,4  +∞   7cos 3sin2 6 π πα α   + = +       tan 12 π α + =   4 2 3− 2 3 4− 4 4 3− 4 3 4− { }na 1 1a = ( )nP n N ∗∈ nP AB nP AC 3:1 ( )1 1 2 1 0,3n n n n nP A a P B a P C++ + + =    10a [0, )+∞ ( )f x 2 ( ) ( ) x xf x f x e ′+ = 1 1( )2 2 2 f e = )(xf ′ ( )f x a b 2 2 2 1 1(sin ) 64 abf a e b θ ≤ + + θ 5[2 ,2 ] [2 ,2 ]6 6k k k k π ππ π π π π+ + + k Z∈ 5[2 ,2 ]6 6k k π ππ π+ + k Z∈ 2[2 ,2 ] [2 ,2 ]3 3k k k k π ππ π π π π+ + + k Z∈ 2[2 ,2 ]3 3k k π ππ π+ + k Z∈ a b ba× θsin⋅⋅=× baba 5,1 == ba 4−=⋅ba ba × 15.已知点 的坐标满足 则 的取值范围是_______________. 16.如下图所示将若干个点摆成三角形图案，每条边（色括两个端点）有 n (n>l，n∈N)个点， 相应的图案 中总的点数记为 ，则 =_____________ [Z#xx 三、解答题:共 70 分，解答应写出文字说明、证明过程或者演算步骤。第 17～21 题为必考 题，每题 12 分,第 22，23 题为选考题，每题 10 分,考生根据要求作答。 17. （本小题满分 12 分） 已知函数 . （Ⅰ）当 时，求 的值域； （Ⅱ）若 的内角 、 、 所对的边分别为 、 、 ，且满足 ,求 的值. 18. （本小题满分 12 分） 如 图 ， 是 圆 的 直 径 ， 是 圆 上 异 于 的 一 点 ， ， ， ， ， . （Ⅰ）求证： ； （Ⅱ）若 ，求平面 与平面 所成的锐二面角的余弦值. ( ) 2 22 3sin cos 3sin cos 3f x x x x x= − − + 0, 2x π ∈   ( )f x ABC∆ A B C a b c ( ) ( )sin 23, 2 2cossin A Cb A Ca A += = + + ( ),P x y 0, , 2 1, x y x y x ≤  ≥  < + 2 2 x y x y + + na 2 3 3 4 4 5 2017 2018 9 9 9 9 a a a a a a a a + + + + ( )f B AB C O C ,A B DO BO⊥ DO EB∥ AO OE⊥ 1DO EB= = 4AB = DE AOD⊥ 平面 AO BO= AED ABE 19.（本小题满分 12 分） 已知数列 前 项和为 ， ，且满足 （ ）． （Ⅰ）求数列 的通项公式； （Ⅱ）若 ，求数列 前 项和为 . 20.（本小题满分 12 分） 已知椭圆 的右焦点 ,椭圆 的左,右顶点分别为 . 过点 的直线 与 椭圆交于 两点,且△ 的面积是△ 的面积的 3 倍. （Ⅰ）求椭圆 的方程； （Ⅱ）若 与 轴垂直， 是椭圆 上位于直线 两侧的动点，且满足 ， 试问直线 的斜率是否为定值，请说明理由． 21.（本小题满分 12 分） 已知函数 [] （Ⅰ）求函数 在点 处的切线方程； （Ⅱ）若存在 ，使得 （ 是自然对数的底数），求实数 的取值范围. { }na n nS 1 2a = − 1 1 12n nS a n+= + + *n N∈ { }na 3log ( 1)n nb a= − + ( ){ }1 n n nb a− ⋅ − n nT 2 2 2 2: 1 ( 0)x y a ba b Γ + = > > (1, 0)F Γ ,M N F l ,C D MCD NCD Γ CD x ,A B Γ CD ACD BCD∠ = ∠ AB 2( ) ln ( 0 1)xf x a x x a a a= + − > ≠且 ( )f x (0, (0))f [ ]1, 2 1,1x x ∈ − 1 2( ) ( ) 1f x f x e− ≥ − e a 22．选修 4-4：坐标系与参数方程 在极坐标系中，曲线 的极坐标方程为 ，以极点为原点，极轴为 轴的 正半轴建立平面直角坐标系，直线 的参数方程为 （ 为参数）. （Ⅰ）写出曲线 的参数方程和直线 的普通方程； （Ⅱ）已知点 是曲线 上一点，求点 到直线 的最小距离. 23．选修 4-5：不等式选讲 已知函数 ， ． （Ⅰ）当 时，求不等式 的解集； （Ⅱ）若对任意的 ，都有 ，使得 成立，求实数 的取值范 围． 汕头市金山中学 2018 届高三理科数学期末考试参考答案 1~12 CDDBC DCCDB AB 13. 14. 15. 16. 17 ： （ Ⅰ ） （Ⅱ） , , 即 ，由正弦定理可得 ( ) ( ) ( ) ( )sin 2 2 2cos , sin 2 2sin 2sin cossin A C A C A C A A A CA + = + + ∴ + = + + ( ) ( ) ( )sin cos cos sin 2sin 2sin cosA A C A A C A A A C∴ + + + = + + ( ) ( )sin cos cos sin 2sinA A C A A C A∴− + + + = sin 2sinC A= C ( )2 21 2sin 3ρ θ+ = x l 6 x t y t =  = + t C l P C P l ( ) ( )2f x x m x m R= − + + ∈ ( ) 2 1 3g x x= − + 1m = ( ) 5f x ≤ 1x R∈ 2x ∈ R ( ) ( )1 2f x g x= m 1− 3 2,1 −  2016 2017 ( ) 2 2 1 cos2 1 cos22 3sin cos 3sin cos 3 3sin 2 3 32 2 x xf x x x x x x − += − − + = − ⋅ − + 73sin 2 +cos2 1 2sin 2 1, 0, , 2 , ,6 2 6 6 6x x x x x π π π π π     = + = + + ∈ ∴ + ∈           ( ) ( ]1sin 2 ,1 , 2sin 2 1 0,3 .6 2 6x f x x π π     ∴ + ∈ − ∴ = + + ∈          ，又由 可得 ，由余弦定理可得 . 由正弦定理可得 ,由三角形的内角和可得 . 18.（1）因为 是圆 的直径， 是圆 上异于 的一点，∴ . 又因为 ，又 ，所以 平面 又因为 ， ，∴四边形 是平行四边形. 所以 平面 （2）由 （ 1 ） 知 ，又 因 为 ，又 ， 所 以 平 面 ， ∴ ,又因为 ， ，所以,以 为原点建立如图所示空间直角坐 标系， 则 ， ， ， . 设 为 平 面 的 法 向 量 ， 则 ， 令 ， 得 . 设 为平面 的法向量，则 ，令 得 . 所以 ， 2c a= 3b a = 3b a= 2 2 2 2 2 23 4 3cos , 302 22 3 2 b c a a a aA Abc a a + − + −= = = ∴ =    sin 2sin 1, 90C A C= = =  ( ) ( )60 , 60 2B f B f= ∴ = =  AB C O C ,A B AO BO⊥ DO BO⊥ AO DO O= BO ⊥ AOD DO EB∥ DO EB= BODE ,BO DE∴ ∥ DE ⊥ AOD AO BO⊥ AO OE⊥ BO OE O= AO ⊥ BOED AO OD⊥ DO BO⊥ AO BO⊥ O (2 2,0,0)A (0,0,1), (0,2 2,0), (0,2 2,1)D B E ( 2 2,0,1), (0,2 2,0),AD DE= − =  ( 2 2,2 2,0)AB = − (0,0,1)BE = 1 ( , , )x y zn = ADE 1 1 2 2 0 2 2 0 AD x z DE y  ⋅ = − + = ⋅ = =   n n 1x = 1 (1,0,2 2)n = 2 1 1 1( , , )x y zn = ABE 2 1 1 2 1 2 2 2 2 0 0 AB x y BE z  ⋅ = − + = ⋅ = =   n n 1 1,x = 2 =(1,1,0)n 1 2 1 2 1 2 1 2cos , | | | | 63 2 ⋅= = =⋅ n nn n n n ∴平面 与平面 所成的锐二面角的余弦值为 . 19. （Ⅰ） ，由 ，得 ， 两式相减得 ， ………………2 分 由 得到 ， 当 ， 又 所以 为以-3 为首项以 3 为公比的等比数列， 故 ………………6 分 （Ⅱ） ， …………7 分 9 分 …………11 分 ………………12 分 20： 解法一：（I）因为△ 的面积是△ 的面积的 3 倍， 所以 ，即 ，所以 ，所以 ， 则椭圆 的方程为 ． ………………………… 4 分 （II）当 ，则 ， 设直线 的斜率为 ，则直线 的斜率为 ， 不妨设点 在 轴上方， ，设 ， ， 则 的直线方程为 ，代入 中整理得 ， AED ABE 2 6 1 2a = − * 1 1 1( N )2n nS a n n+= + + ∈ 1 1 ( 2)2n nS a n n− = + ≥ 13 2n na a += + ( 2)n ≥ 13 2n na a += + 13( 1) 1n na a +− = − 1n = 时 1 2 2 1 1 2 1 2, 2 4 8, 3( 1) 12a a a a a a= + ∴ = − = − − = −满足 1 1 3 0,a − = − ≠ { 1}na − 11 ( 3) 3 3 .n n na −− = − ⋅ = − 3 1.n na = − + 3 3log ( 1) log 3n n nb a n= − + = = ( ) ( )1 1 3 1n n n n nb a n− ⋅ − = − ⋅ + − ( ) ( ) ( )( ) ( )1 2 1 3 1 3 1 2 3 4 1 3 3 3 2 1 3 3 3 2 n n n n nn T n n n n n+ − = − + + − + + + − − + + + + + − = + −  − − −=  当 为偶数时， ( ) 13 1 31 3 3 4= 2 1 3 2 n n n n nn T n n +−− − −− + − =−当 为奇数时， 1 1 3 3 2= 3 3 4 2 n n n n n T n n + +  − −  − −  为偶数， 为奇数. ， 综上， ， MCD NCD 3MF NF= ( )3a c a c+ = − 2 2a c= = 2 3b = Γ 2 2 14 3 x y+ = ACD BCD∠ = ∠ 0AC BCk k+ = AC k BC k− C x 31, 2C      A ( )1 1,x y B ( )2 2,x y AC ( )3 12y k x− = − 2 2 14 3 x y+ = ( ) ( )2 2 23 4 4 2 3 4 12 3 0k x k k x k k+ − − + − − = ； 同理 ． ……………………8 分 所以 ， ， …………………… 10 分 则 ， 因此直线 的斜率是定值 ．…………………………12 分 解法二： （II）依题意知直线 的斜率存在，所以设 方程： 代入 中 整理得 ，设 ， ， 所以 ， ，……………………6 分 当 ，则 ，不妨设点 在 轴上方， ， 所以 ，整理得 ，…………… 8 分 所以 ， 整理得 ，……………………9 分 即 ，所以 或 ．…………………… 10 分 当 时 ， 直 线 过 定 点 ， 不 合 题 意 ； 当 时 ， ( ) ( )1 2 4 2 31 3 4 k kx k −+ = + ( ) ( )2 2 4 2 31 3 4 k kx k ++ = + ( ) 2 1 2 2 8 6 3 4 kx x k −+ = + ( )1 2 2 24 3 4 kx x k −− = + 1 2 1 2 AB y yk x x −= − ( )1 2 1 2 2k x x k x x + −= − 1 2 = AB 1 2 AB AB y kx m= + 2 2 14 3 x y+ = 2 2 2(4 3) 8 4 12 0k x kmx m+ + + − = A ( )1 1,x y B ( )2 2,x y 1 2 2 8 4 3 kmx x k + = − + 2 1 2 2 4 12 4 3 mx x k −= + 2 2 2 2 2 264 4(4 3)(4 12) 16(12 3 9) 0k m k m k m∆ = − + − = − + > ACD BCD∠ = ∠ 0AC BCk k+ = C x 31, 2C      1 2 1 2 3 3 2 2 01 1 y y x x − − + =− − 1 2 1 2 32 ( )( ) 2 3 02kx x m x x m+ − + − + = 2 2 2 4 12 3 82 ( )( ) 2 3 04 3 2 4 3 m kmk m mk k −⋅ + − − − + =+ + 212 12( 2) 9 6 0k m k m+ − + − = (6 3)(2 2 3) 0k k m− + − = 2 2 3 0k m+ − = 6 3 0k − = 2 2 3 0k m+ − = AB 31, 2C      6 3 0k − = ，符合题意， 所以直线 的斜率是定值 ．…………………………12 分 21.解：（I）因为函数 ， 所以 ， ，…………………………………………2 分 又因为 ，所以函数 在点 处的切线方程为 ． …………3 分 （II）因为存在 ，使得 成立， 而当 时， ， 所以只要 即可．……………………………………………4 分 由（I）， ． 得 因 为 当 时 ， 总 有 所 以 在 上 是 增 函 数， ………………………………5 分 又 ， 所以 ， ， 的变化情况如下表所示： 减函数 极小值 增函数 所以 在 上是减函数，在 上是增函数， 所以当 时， 的最小值 ， 的最大值 为 和 中的最大值．………………………7 分 因为 ， 令 ，因为 ， 所以 在 上是增函数． 1 2k = AB 1 2 2( ) ln ( 0, 1)xf x a x x a a a= − > ≠+ ( ) ln 2 lnxf x a a x a′ = −+ (0) 0f ′ = (0) 1f = ( )f x (0, (0))f 1y = 1 2, [ 1,1]x x ∈ − 1 2( ) ( ) e 1f x f x− −≥ [ 1,1]x∈ − 1 2 max min( ) ( ) ( ) ( )f x f x f x f x− −≤ max min( ) ( ) e 1f x f x− −≥ ( ) ln 2 ln 2 ( 1)lnx xf x a a x a x a a′ = − = −+ + ( )2( ) 2 ln xf x a a′′ = ⋅+ 0, 1a a> ≠ ( ) 0,f x′′ > ( )f x′ R (0) 0f ′ = x ( )f x′ ( )f x x ( ,0)−∞ 0 (0, )∞+ ( )f x′ − 0 + ( )f x ( )f x [ 1,0]− [0,1] [ 1,1]x∈ − ( )f x ( ) ( )min 0 1f x f= = ( )f x ( )maxf x ( )1f − ( )1f 1 1(1) ( 1) ( 1 ln ) ( 1 ln ) 2lnf f a a a a aa a − − = − − = − −+ + + 1( ) 2ln ( 0)g a a a aa = − − > 2 2 1 2 1( ) 1 (1 ) 0g a a a a ′ = − = − >+ 1( ) 2lng a a aa = − − ( ) ( )0,1 1 +a∈ ∞、 ， 而 ，故当 时， ，即 ； 当 时， ，即 ．………………………………………9 分 所以，当 时， ，即 ， 函数 在 上是增函数，解得 ；………………………………10 分 当 时， ，即 ， 函数 在 上是减函数，解得 ．……………………………… 11 分 综上可知，所求 的取值范围为 ．………………………………12 分 21.(Ⅰ)由曲线 的极坐标方程得： ， ∴曲线 的直角坐标方程为: ，曲线 的参数方程为 ,（ 为参 数）； 直线 的普通方程为： . (II)设曲线 上任意一点 为 ，则 点 到直线 的距离为 ∴ . 22.（Ⅰ）当 时， ， ① 当 时 ， ， 由 ， 解 得 ， 所 以 ； ②当 时， 恒成立，所以 ； ③当 时， ，由 ，解得 ，所以 ； (1) 0g = 1a > ( ) 0g a > (1) ( 1)f f> − 0 1a< < ( ) 0g a < (1) ( 1)f f< − 1a > (1) (0) e 1f f− −≥ ln e 1a a− −≥ lny a a= − (1, )a∈ +∞ ea≥ 0 1a< < ( 1) (0) e 1f f− − −≥ 1 ln e 1aa + −≥ 1 lny aa = + (0,1)a∈ 10 ea< ≤ a 1(0, ] [e, )ea∈ ∞+ C 2 2 22 sin 3ρ ρ θ+ = C 2 2 13 x y+ = C 3{ x cos y sin α α = = α l 6y x− = C P ( )3cos ,sinα α P l 2cos 63cos sin 6 6 2 2 d παα α  + + − +  = = min 2 2d = 1m = ( ) 1 2f x x x= − + + 2x ≤ − ( ) 1 2 2 1f x x x x= − − − = − − 2 1 5x− − ≤ 3x ≥ − 3 2x− ≤ ≤ − 2 1x− < < ( ) 1 2 3 5f x x x= − + + = ≤ 2 1x− < < 1x ≥ ( ) 1 2 2 1f x x x x= − + + = + 2 1 5x + ≤ 2x ≤ 1 2x≤ ≤ 综上所述，不等式 的解集为 ． （II）若对任意的 ，都有 ，使得 成立， 设 ， ，则 ， 因为 ， ， 所以 ，解得 或 ， 因此，实数 的取值范围为 ． ( ) 5f x ≤ [ ]3,2− 1x R∈ 2x R∈ ( ) ( )1 2f x g x= ( ){ }|A y y f x= = ( ){ }|B y y g x= = A B⊆ ( ) ( ) ( )2 2 2f x x m x x m x m= − + + ≥ − − + = + ( ) 2 1 3 3g x x= − + ≥ 2 3m + ≥ 1m ≥ 5m ≤ − m ] [( ), 5 1,−∞ − ∪ +∞