- 2021-04-20 发布 |
- 37.5 KB |
- 2页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级下册数学同步练习4-5 第2课时 建立一次函数模型解决预测类型的实际问题 湘教版
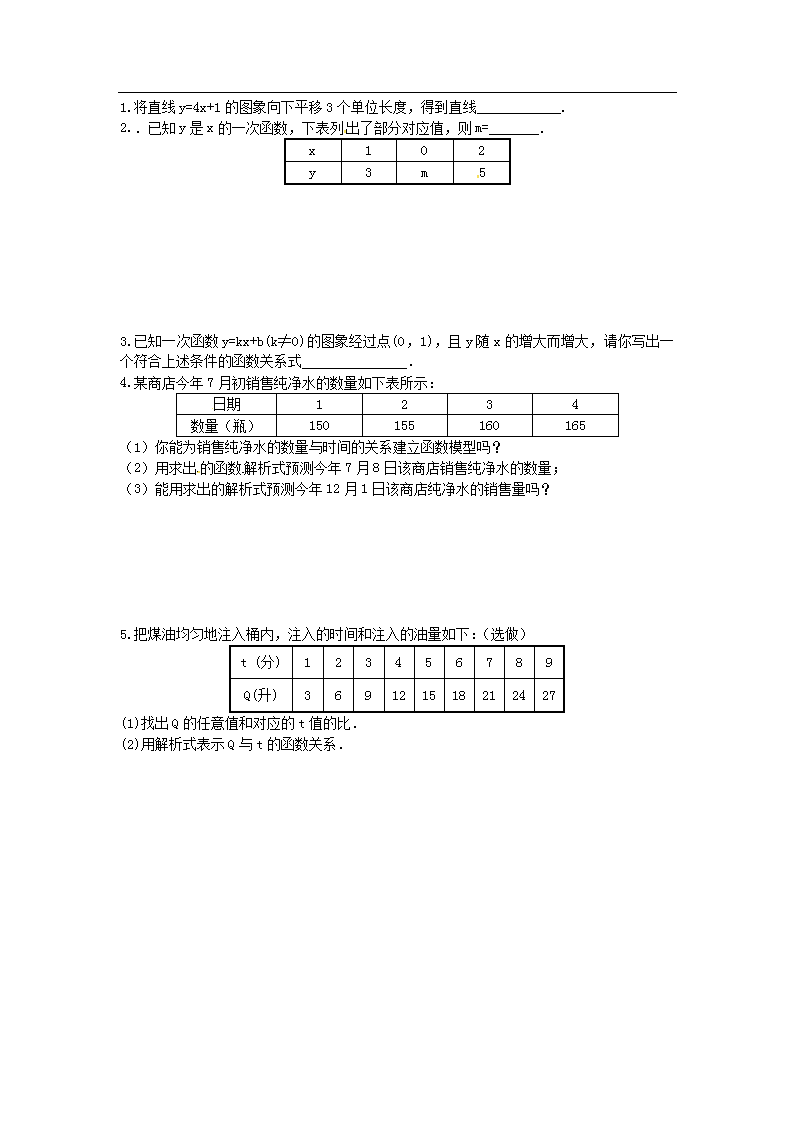
第2课时 建立一次函数模型解决预测类型的实际问题 学习目标: 1.能用一次函数的知识解决简单的实际问题. 2.能结合对函数关系的分析,尝试对变量的变化规律进行初步预测. 3、感受一次函数的应用价值,乐于运用所学知识去解决实际问题,体验成功,增强自信. 学习重点:建立一次函数模型,结合对函数关系的分析,对变量的变化规律作出初步预测. 学习难点:建立一次函数模型 学习过程: 一、复习导入: [来源:学|科|网] 1、回忆利用待定系数法求函数解析式的步骤 已知一次函数经过两点(1,3),(2,0),求这个函数的解析式. 2、温度的度量有两种:摄氏温度和华氏温度,水的沸点是100℃,用华氏温度度量为212F,水的冰点是0℃,用华氏温度度量为32F,已知摄氏度与华氏温度的关系可近似为一次函数,你能不能想出办法,方便地把华氏温度换算成摄氏温度? 二、 师生合作,探究新知: 解决导入中的问题2 三、检查学习效果 1.“练习” (1)把温度84华氏温度换算成摄氏温度. (2) 已知正比例函数的图像经过点M(-1,5).求这个函数解析式. (3) 已知一次函数经过两点(-1,3),(2,-5),求这个函数的解析式 2.例题点拨:[来源:Zxxk.Com] 如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距,某项研究表明,一般情况下人的身高h是指距d的一次函数,下表是测得的指距、身高的一组数据. 指距d(cm) 20 2l 22 23 身高h(cm) 160 169[来源:学科网] 178 187 (1)求出h与d之间的函数关系式(不要求写出自变量d的取值范围). (2)某人身高为196cm,一般情况下他的指距应是多少? 五、归纳小结:这节课你有什么收获,还有什么疑惑? 六、当堂训练: 1.将直线y=4x+1的图象向下平移3个单位长度,得到直线 . 2..已知y是x的一次函数,下表列出了部分对应值,则m= . x 1 O 2 y 3 m 5 3.已知一次函数y=kx+b(k≠O)的图象经过点(0,1),且y随x的增大而增大,请你写出一个符合上述条件的函数关系式 . 4.某商店今年7月初销售纯净水的数量如下表所示: 日期 1 2 3 4 数量(瓶) 150 155 160 165 (1)你能为销售纯净水的数量与时间的关系建立函数模型吗? (2)用求出的函数解析式预测今年7月8日该商店销售纯净水的数量; (3)能用求出的解析式预测今年12月1日该商店纯净水的销售量吗? [来源:学|科|网] 5.把煤油均匀地注入桶内,注入的时间和注入的油量如下:(选做) t (分) 1 2 3 4 5 6 7 8 9 Q(升) 3 6 9 12 15 18 21 24 27 (1)找出Q的任意值和对应的t值的比. (2)用解析式表示Q与t的函数关系. [来源:Z&xx&k.Com]查看更多