数学文卷·2018届山东省烟台一中、二中（烟台市）高二下学期期中考试（2017-04）

数学文卷·2018届山东省烟台一中、二中（烟台市）高二下学期期中考试（2017-04）

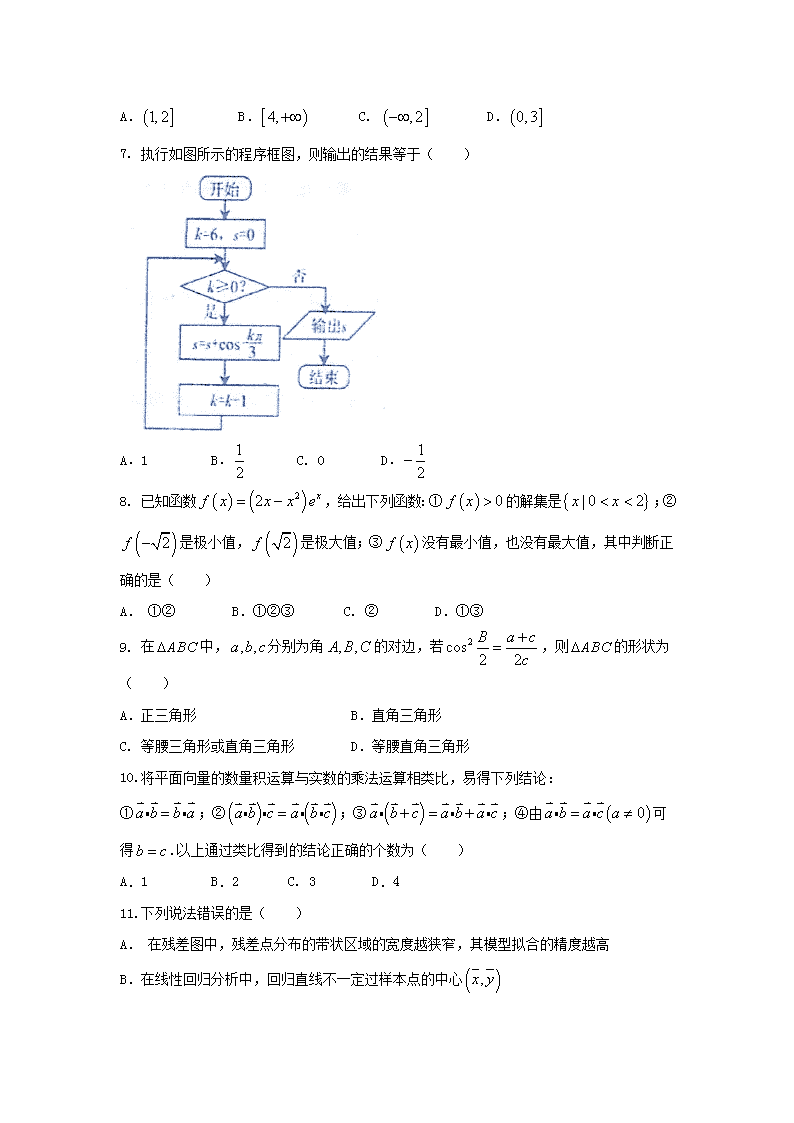
山东省烟台市2016-2017学年高二下学期期中学段考试 文科数学 一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.设的实部与虚部相等，其中为实数，则（ ）‎ A．-1 B．-2 C．2 D．1‎ ‎2. 下面几种推理是合情推理的是 （ ）‎ ‎①由圆的性质类比出球的有关性质 ‎②由直角三角形、等腰三角形、等边三角形内角和是180°归纳出所有三角形的内角和都是180°‎ ‎③某次考试张军成绩是100分，由此推出全班同学成绩都是100分 ‎④数列1，0，1，0，…，推测出每项公式 A． ①② B．①③④ C．①②④ D．②④‎ ‎3. 已知函数，若恒成立，则实数的取值范围是（ ）‎ A． B． C． D．‎ ‎ 4.观察两个变量（存在线性相关关系）得如下数据：‎ ‎-10‎ ‎-6.99‎ ‎-5.01‎ ‎-2.98‎ ‎3.98‎ ‎5‎ ‎7.99‎ ‎8.01‎ ‎-9‎ ‎-7‎ ‎-5‎ ‎-3‎ ‎4.01‎ ‎4.99‎ ‎7‎ ‎8‎ 则两变量间的线性回归方程为（ ）‎ A． B． C. D．‎ ‎5. 已知数列的前项和为，且，可归纳猜想出的表达式为（ ）‎ A． B． C. D．‎ ‎6. 设函数在区间上单调递减，则实数的取值范围是 （ ）‎ A． B． C. D．‎ ‎7. 执行如图所示的程序框图，则输出的结果等于（ ）‎ A．1 B． C. 0 D．‎ ‎8. 已知函数，给出下列函数：①的解集是；②是极小值，是极大值；③没有最小值，也没有最大值，其中判断正确的是（ ）‎ A． ①② B．①②③ C. ② D．①③‎ ‎9. 在中，分别为角的对边，若，则的形状为（ ）‎ A．正三角形 B．直角三角形 ‎ C. 等腰三角形或直角三角形 D．等腰直角三角形 ‎10.将平面向量的数量积运算与实数的乘法运算相类比，易得下列结论：‎ ‎①；②；③；④由可得.以上通过类比得到的结论正确的个数为（ ）‎ A．1 B．2 C. 3 D．4‎ ‎11.下列说法错误的是（ ）‎ A． 在残差图中，残差点分布的带状区域的宽度越狭窄，其模型拟合的精度越高 ‎ B．在线性回归分析中，回归直线不一定过样本点的中心 ‎ C. 在回归分析中，为0.98的模型比为0.80的模型拟合的效果好 ‎ D．自变量取值一定时，因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系 ‎12. 定义在上的单调递减函数，若的导函数存在且满足，则下列不等式成立的是（ ）‎ A． B． C. D．‎ 二、填空题：本大题共4小题，每小题5分，满分20分，将答案填在答题纸上 ‎13. 若复数为实数，则实数的值为 ．‎ ‎14.已知，则与的大小关系为 ．‎ ‎15.若下列两个方程中至少有一个方程有实数根，则实数的取值范围是 .‎ ‎16. 若，且，则 ．‎ 三、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤. ‎ ‎17. 已知复数满足.‎ ‎（1）求复数的共轭复数；‎ ‎（2）若，且复数对应向量的模不大于复数所对应向量的模，求实数的取值范围.‎ ‎18. 已知，利用分析法证明：.‎ ‎19. 某种产品的年销售量与该年广告费用支出有关，现收集了4组观测数据列于下表：‎ ‎（万元）‎ ‎1‎ ‎4‎ ‎5‎ ‎6‎ ‎（万元）‎ ‎30‎ ‎40‎ ‎60‎ ‎50‎ 现确定以广告费用支出为解释变量，销售量为预报变量对这两个变量进行统计分析.‎ ‎（1）已知这两个变量满足线性相关关系，试建立与之间的回归方程；‎ ‎（2）假如2017年广告费用支出为10万元，请根据你得到的模型，预测该年的销售量.‎ ‎（线性回归方程系数公式）.‎ ‎20. 已知函数，其中.‎ ‎（1）当时，求曲线在点处的切线方程；‎ ‎（2）当时，求函数的单调区间与极值.‎ ‎21.一项针对人们休闲方式的调查结果如下：受调查对象总计124人，其中女性70人，男性54人.女性中有43人主要的休闲方式是看电视，另外27人主要的休闲方式是运动；男性中有21人主要的休闲方式是看电视，另外33人主要的休闲方式是运动.‎ ‎（1）根据以上数据建立一个的列联表；‎ ‎（2）根据下列提供的独立检验临界值表，你最多能有多少把握认为性别与休闲方式有关系？‎ 独立检验临界值表：‎ ‎0.50‎ ‎0.40‎ ‎0.25‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ ‎0.455‎ ‎0.708‎ ‎1.323‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ 参考公式：.‎ ‎22. 设函数，.‎ ‎（1）求的单调区间和最小值；‎ ‎（2）讨论与的大小关系；‎ ‎（3）求的取值范围，使得对任意成立.‎ 参考答案与评分标准 一、 选择题 ‎1---5ACABA 6---10 AAABB 11---12 BA 二、填空题 ‎13、4 14、 15、 16、10‎ 三、解答题 ‎17、解析： ⑴，所以复数的共轭复数为 ‎ ⑵ 复数对应向量为 ‎ 此时 ‎ 又复数对应的向量 ‎ ‎ ‎ 即 实数的取值范围为 ‎ ‎18、解析：要证 只需证 ‎ 因为，所以不等式两边均大于零 因此只需证，‎ 即证 ‎ 只需证 ‎ 只需证，即证 ‎ 只需证，而显然成立，所以原不等式成立. ‎ ‎19、‎ 解：（1）， ，‎ ‎， ‎ ‎ ‎ 所求回归直线方程为. ‎ ‎（2）由已知得时，（万元） ‎ 可预测该年的销售量为75万元. ‎ ‎20、解（1）当时，，此时，‎ 所以 ‎ 又因为切点为，所以切线方程 曲线在点处的切线方程为 ‎（2）由于，‎ 所以 ‎ 由，得 ‎ ‎ (1)当时，则，易得在区间，内为减函数，‎ 在区间为增函数，故函数在处取得极小值 函数在处取得极大值 ‎ （2） 当时，则,易得在区间，内为增函数，‎ 在区间为减函数，故函数在处取得极小值；‎ 函数 在处取得极大值 ‎ ‎21、解、‎ ‎(1)列联表如下：‎ 看电视 运动 合计/人 女性/人 ‎43‎ ‎27‎ ‎70‎ 男性/人 ‎21‎ ‎33‎ ‎54‎ 合计/人 ‎64‎ ‎60‎ ‎124‎ ‎ (2)假设“休闲方式与性别无关”，‎ 由公式算得K2＝≈6.201， ‎ 比较P(K2≥5.024)≈0.025， ‎ 所以有理由认为假设“休闲方式与性别无关”是不合理的，即在犯错误的概率不超过0.025的前提下认为“休闲方式与性别有关”． ‎ ‎22、解析：‎ ‎⑴由题设知，，‎ 所以，令的 ‎ 当时，，故是的单调递减区间 当时，，故是的单调递增区间 ‎ 因此，是的唯一极值点，且为极小值点，从而是最小值点 所以最小值为 ‎ ‎⑵‎ 设则 因为，所以在单调递减、 ‎ 又因为当时，‎ 所以当时，，即 当时，，即 ‎ 当时 ‎ ‎⑶由⑴知的最小值为1‎ 所以，即对恒成立 ‎ 所以即，从而得 ‎