解直角三角形及其应用教案

解直角三角形及其应用教案

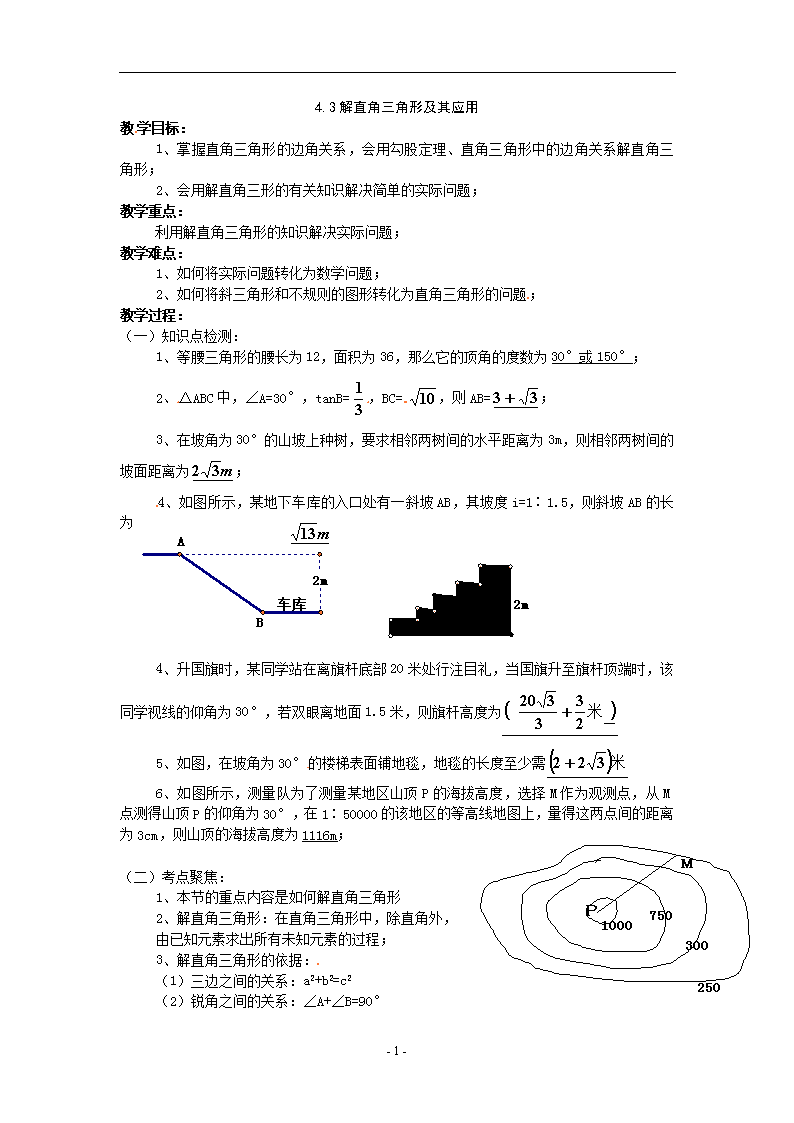
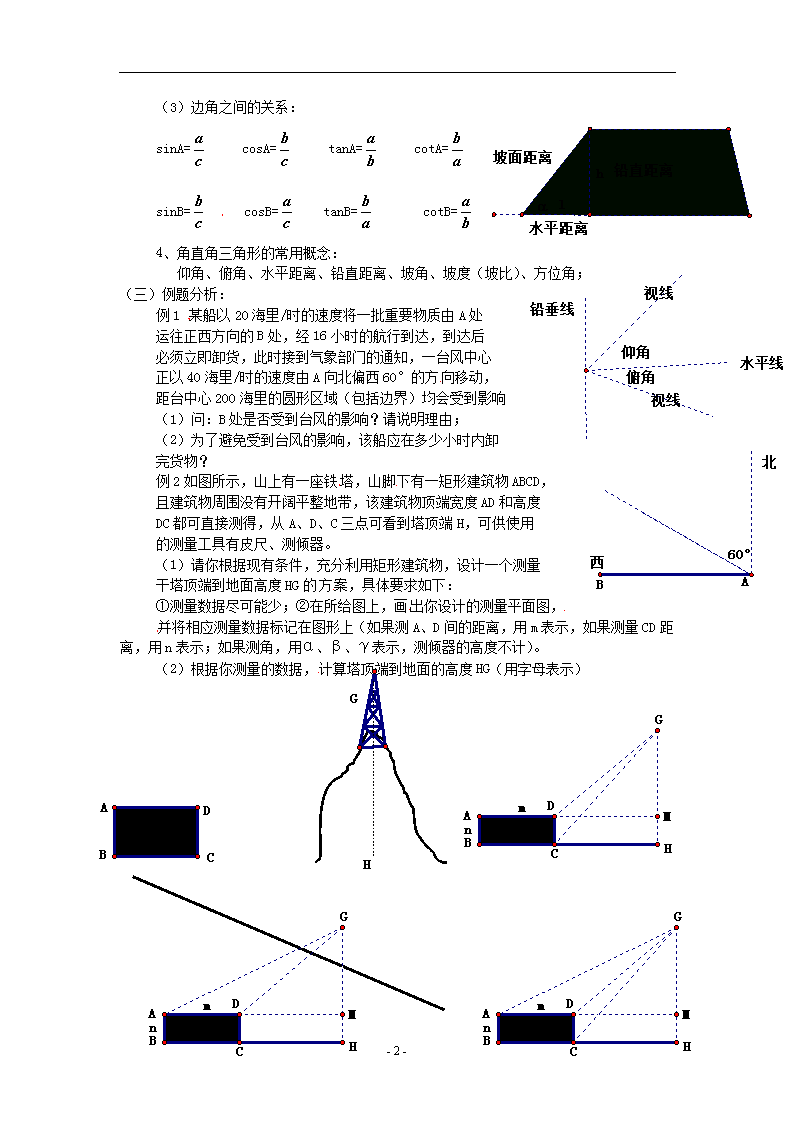
‎4.3解直角三角形及其应用 教学目标：‎ ‎1、掌握直角三角形的边角关系，会用勾股定理、直角三角形中的边角关系解直角三角形；‎ ‎2、会用解直角三形的有关知识解决简单的实际问题；‎ 教学重点：‎ ‎ 利用解直角三角形的知识解决实际问题；‎ 教学难点：‎ ‎1、如何将实际问题转化为数学问题；‎ ‎2、如何将斜三角形和不规则的图形转化为直角三角形的问题；‎ 教学过程：‎ ‎（一）知识点检测：‎ ‎1、等腰三角形的腰长为12，面积为36，那么它的顶角的度数为30°或150°；‎ ‎2、△ABC中，∠A=30°，tanB=，BC=，则AB=；‎ ‎3、在坡角为30°的山坡上种树，要求相邻两树间的水平距离为3m，则相邻两树间的坡面距离为；‎ ‎4、如图所示，某地下车库的入口处有一斜坡AB，其坡度i=1∶1.5，则斜坡AB的长为 ‎4、升国旗时，某同学站在离旗杆底部20米处行注目礼，当国旗升至旗杆顶端时，该同学视线的仰角为30°，若双眼离地面1.5米，则旗杆高度为 ‎5、如图，在坡角为30°的楼梯表面铺地毯，地毯的长度至少需 ‎6、如图所示，测量队为了测量某地区山顶P的海拔高度，选择M作为观测点，从M点测得山顶P的仰角为30°，在1∶50000的该地区的等高线地图上，量得这两点间的距离为3cm，则山顶的海拔高度为1116m；‎ ‎（二）考点聚焦：‎ ‎1、本节的重点内容是如何解直角三角形 ‎2、解直角三角形：在直角三角形中，除直角外，‎ 由已知元素求出所有未知元素的过程；‎ ‎3、解直角三角形的依据：‎ ‎（1）三边之间的关系：a2+b2=c2‎ ‎（2）锐角之间的关系：∠A+∠B=90°‎ - 3 -‎ ‎（3）边角之间的关系：‎ sinA= cosA= tanA= cotA=‎ sinB= cosB= tanB= cotB=‎ ‎4、角直角三角形的常用概念：‎ ‎ 仰角、俯角、水平距离、铅直距离、坡角、坡度（坡比）、方位角；‎ ‎（三）例题分析：‎ 例1 某船以20海里/时的速度将一批重要物质由A处 运往正西方向的B处，经16小时的航行到达，到达后 必须立即卸货，此时接到气象部门的通知，一台风中心 正以40海里/时的速度由A向北偏西60°的方向移动，‎ 距台中心200海里的圆形区域（包括边界）均会受到影响 ‎（1）问：B处是否受到台风的影响？请说明理由；‎ ‎（2）为了避免受到台风的影响，该船应在多少小时内卸 完货物？‎ 例2如图所示，山上有一座铁塔，山脚下有一矩形建筑物ABCD，‎ 且建筑物周围没有开阔平整地带，该建筑物顶端宽度AD和高度 DC都可直接测得，从A、D、C三点可看到塔顶端H，可供使用 的测量工具有皮尺、测倾器。‎ ‎（1）请你根据现有条件，充分利用矩形建筑物，设计一个测量 干塔顶端到地面高度HG的方案，具体要求如下：‎ ①测量数据尽可能少；②在所给图上，画出你设计的测量平面图，‎ 并将相应测量数据标记在图形上（如果测A、D间的距离，用m表示，如果测量CD距离，用n表示；如果测角，用α、β、γ表示，测倾器的高度不计）。‎ ‎（2）根据你测量的数据，计算塔顶端到地面的高度HG（用字母表示）‎ ‎ ‎ ‎ ‎ ‎ ‎ - 3 -‎ ‎(四)课堂小结:‎ ‎1、把实际问题转化为数学问题,这个转化有两个方面:一是将实际图形转化为几何图形,画出正确的平面或截面示意图,二是将已知条件转化为示意图中的边、角或它们之间的关系;‎ ‎2、把数学问题转化为解直角三角形问题,如果示意图不是直角三角形,可添加适当的辅助线,画出直角三角形.‎ ‎(五)课堂作业:‎ 同步练习相关内容 - 3 -‎