- 2021-04-20 发布 |
- 37.5 KB |
- 14页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
内蒙古赤峰市2020届高三四月模拟考试文科数学试题附答案
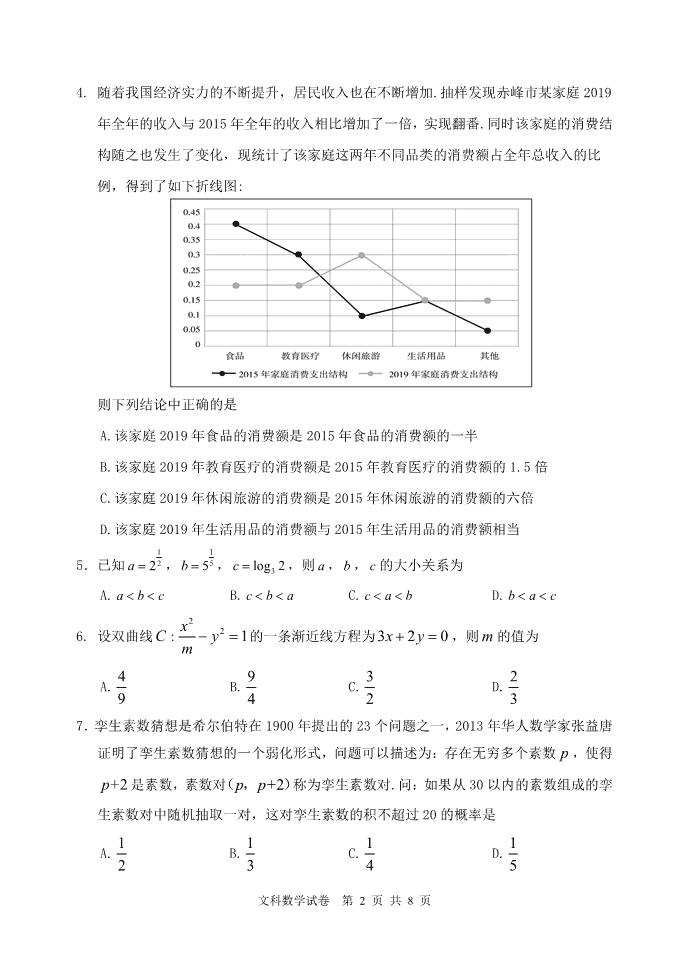
文科数学试卷 第 1 页 共 8 页 绝密★启用前 赤峰市高三 4·20 模拟考试试题 文科数学 2020.4 本试卷共 23 题,共 150 分,共 8 页。考试结束后,将本试卷和答题卡一并交回。 注意事项: 1.答题前,考生先将自己的姓名,准考证号码填写清楚,将条形码粘贴在条形码区 域内. 2.选择题必须使用 2B 铅笔填涂;非选择题必须使用 0.5 毫米的黑色字迹的签字笔 书写,字体工整,笔迹清楚. 3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无 效;在草稿纸、试卷上答题无效. 4.作图可先使用铅笔画出,确定后必须黑色字迹的签字笔描黑. 5.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀. 一、选择题:本大题共 12 小题,每小题 5 分,共 60 分.在每小题给出的四个选项中,只 有一项是符合题目要求的. 1. 已知集合 022 xxxA , xyxB 1 ,则 BA = A. 2, B. 1, C. 1,1 D. 2,1 2. 设复数 z 在复平面上的对应点为 1,1 , z 为 z 的共轭复数,则 A. z z 是纯虚数 B. z z 是实数 C. z z 是纯虚数 D. z z 是纯虚数 3. “ 0x y ”是“ lg( +1) lg( 1)x y ”成立的 A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 文科数学试卷 第 2 页 共 8 页 4. 随着我国经济实力的不断提升,居民收入也在不断增加.抽样发现赤峰市某家庭 2019 年全年的收入与 2015 年全年的收入相比增加了一倍,实现翻番.同时该家庭的消费结 构随之也发生了变化,现统计了该家庭这两年不同品类的消费额占全年总收入的比 例,得到了如下折线图: 则下列结论中正确的是 A.该家庭 2019 年食品的消费额是 2015 年食品的消费额的一半 B.该家庭 2019 年教育医疗的消费额是 2015 年教育医疗的消费额的 1.5 倍 C.该家庭 2019 年休闲旅游的消费额是 2015 年休闲旅游的消费额的六倍 D.该家庭 2019 年生活用品的消费额与 2015 年生活用品的消费额相当 5.已知 1 22a , 1 55b , 3log 2c ,则 a , b , c 的大小关系为 A. a b c B. c b a C. c a b D. b a c 6. 设双曲线 C : 2 2 1x ym 的一条渐近线方程为3 2 0x y ,则 m 的值为 A. 4 9 B. 9 4 C. 3 2 D. 2 3 7.孪生素数猜想是希尔伯特在 1900 年提出的 23 个问题之一,2013 年华人数学家张益唐 证明了孪生素数猜想的一个弱化形式,问题可以描述为:存在无穷多个素数 p ,使得 +2p 是素数,素数对 +2p p( , )称为孪生素数对.问:如果从 30 以内的素数组成的孪 生素数对中随机抽取一对,这对孪生素数的积不超过 20 的概率是 A. 1 2 B. 1 3 C. 1 4 D. 1 5 文科数学试卷 第 3 页 共 8 页 8.设等比数列{ }na 的前 n 项和为 nS ,若 1 1a ,且 2 3 4,2 ,4a a a 成等差数列,则 8 =S A.510 B. 255 C.512 D. 256 9. 将函数 2 1sin cos cos 2y x x x 的图像向右平移 8 个单位长度得到函数 ( )g x 的 图像,下列结论正确的是 A. ( )g x 是最小正周期为 2 的偶函数 B. ( )g x 是最小正周期为 4 的奇函数 C. ( )g x 在 ,2 上单调递减 D. ( )g x 在 0, 2 上的最大值为 2 2 10.已知椭圆C : 19 2 2 2 2 a y a x , 21 FF、 是其左右焦点,若对椭圆C 上的任意一点 P , 都有 021 PFPF 恒成立,则实数 a 的取值范围为 A. 3 0 (0,3) ( ,) B. 3,0 0,3 C. ( , 3) (3, ) D. ( , 3] [3, ) 11. 已知三棱锥 P ABC 中, 3PA PB PC ,当三棱锥 P ABC 体积最大值时, 三棱锥 P ABC 的外接球的体积为 A. 9 2 B.36 C. 32 71 D. 2 9 12. 已知函数 eexxy ,1ln21 的图象上存在点 M ,函数 axy 2 的图象上 存在点 N ,且点 NM , 关于原点对称,则实数 a 的取值范围是 A. 2 11,0 e B. 30 2 e, C. 311 2 2 ee , D. ,11 2e 二、填空题:本大题共 4 小题,每小题 5 分,共 20 分. 13. 设 )(xf 在 R 上是奇函数,且 (1 ) (1 )f x f x ,当 (0,1)x 时, 3)( xxf = ,则 =)2 7(f . 文科数学试卷 第 4 页 共 8 页 14. 已知非零向量 ,a b 满足 =2b a ,且 b a a ,则 a 与b 的夹角为 . 15.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有仓,广 三丈,袤四丈五尺,容粟一万斛,问高几何?”其意思为:“今有一个长方体的粮仓, 宽 3 丈,长 4 丈 5 尺,可装粟一万斛.已知 1 斛粟的体积为 2.7 立方尺,1 丈为 10 尺,则该粮仓的高是________尺.若将这些粟装入一个圆柱形粮仓内,若使这个圆柱 形粮仓的表面积(含上下两底)最小,那么它的底面半径是___________ 尺. 16.设数列{ }na 的前 n 项和为 nS ,且满足 2 1n na S ,则使 2 2 2 1 1 2 5+ + + 23 n na a a 成立 的 n 的最大值为 . 三、解答题:共 70 分。解答应写出文字说明,证明过程或演算步骤。第 17~21 题为必 考题,每个试题考生都必须作答,第 22~23 题为选考题,考生根据要求作答. (一)必考题:共 60 分 17.(12 分) 如图,四棱锥 P ABCD 中,底面 ABCD 为直角梯形, AB AD =45ADC , / /AD BC , 2 2AD AB , ADP 为等边三角形,平面 PAD 底面 ABCD ,E 为 AD 的中点. (1)求证:平面 PBC 平面 PCE ; (2)点 F 在线段CD 上,且 3= 2 CF FD , 求三棱锥 F ABP 的体积. 文科数学试卷 第 5 页 共 8 页 18.(12 分) 在 ABC 中,内角 A , B ,C 所对的边分别是 cba ,, ,且 cos 3 sinb c a B a B (1)求角 A ; (2)若 2 3a ,求 ABC 的面积的最大值. 文科数学试卷 第 6 页 共 8 页 19.(12 分) 3 月 3 日,武汉大学人民医院的团队在预印本平台 SSRN 上发布了一项研究:在新冠肺 炎病例的统计数据中,男性患者往往比女性患者多。研究者分析了 1 月 1 日~29 日的 6013 份病例数据,发现 55.9%的患者为男性;进入重症监护病房的患者中,则有 58.8% 为男性。随后,他们分析了武汉大学人民医院的数据。他们按照症状程度的不同进行 分析,结果发现,男性患者有 11.8%为危重,而女性患者危重情况的为 7%。也就是说, 男性的发病情况似乎普遍更严重。研究者总结道:“男性在新冠肺炎的传播中扮演着 重要的角色。” 那么,病毒真的偏爱男性吗? 有一个中学生学习小组,在自己封闭的社区进行无接触抽样问卷调查,收集到男、女 患者各 50 个数据,统计如下: 轻-中度感染 重度(包括危重) 总计 男性患者 20 女性患者 30 总计 50 50 100 (1)求 2 2 列联表中的数据 , , ,m n x y 的值; (2)能否有99.9%把握认为,新冠肺炎的感染程度和性别有关?(3)该学生实验小 组打算从“轻-中度感染”的患者中按男女比例再抽取 5 人,追踪某种中药制剂 的效果。然后从这 5 人中随机抽取 3 人进行每日的健康记录,求至少抽到 2 名 女性患者的概率. 附表及公式: 2 2 ( ) ( )( )( )( ) n ad bcK a b c d a c b d , n a b c d . 2 0( )P K k 0.05 0.025 0.010 0.005 0.001 0k 3.841 5.024 6.635 7.879 10.828 文科数学试卷 第 7 页 共 8 页 20.(12 分) 已知曲线C 上的任意一点 M 到点 )1,0(F 的距离比到直线 2: yl 的距离少 1,动 点 P 在直线 1: ys 上,过点 P 作曲线C 的两条切线 ,PA PB ,其中 ,A B 为切点. (1)求曲线C 的方程; (2)判断直线 AB 是否能恒过定点?若能,求定点坐标;若不能,说明理由. 21.(12 分) 已知函数 xxaxaxf ln12 2 (1)当 0a 时,求函数 xf 的极值; (2)当 0a 时,求函数 xf 在 14 1, 上的最小值. 文科数学试卷 第 8 页 共 8 页 (二)选考题:共 10 分.请考生在第 22、23 二题中任选一题做答,如果多做,则按所做 的第一题计分. 做答时,用 2B 铅笔在答题卡上把所选题目对应的标号涂黑. 22. (10 分)选修 4-4:坐标系与参数方程 在平面直角坐标系 xOy 中,直线l 的参数方程为 2x a t y t (t 为参数),以坐标原 点为极点,x 轴正半轴为极轴建立极坐标系,曲线 C 的极坐标方程为 2 2 12 3 sin . (1)若 2a ,求曲线C 与l 的交点坐标; (2)过曲线C 上任意一点 P 作与l 夹角为 45o 的直线,交l 于点 A ,且 PA 的最大值 为 10 ,求 a 的值. 23.(10 分)选修 4—5:不等式选讲 已知函数 ( ) 1 2f x x x . (1)解不等式 1)( xf ; (2)记函数 )(xf 的最大值为 s ,若 ( , , 0)a b c s a b c , 证明: 2 2 2 2 2 2 3a b b c c a abc . 文科数学答案 第 1 页 共 1 页 赤峰市高三 4·20 模拟考试试题 文科数学参考答案 2020.4 说明: 一、本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据 试题的主要考查内容比照评分标准制订相应的评分细则. 二、解答右端所注分数,表示考生正确做到这一步应得的累加分数. 三、只给整数分数,选择题和填空题不给中间分. 一、选择题:本大题共 12 小题,每小题 5 分,共 60 分 1. C; 2.D; 3. A ; 4. C ; 5. B; 6. A; 7. C; 8.B ; 9. D ; 10. C; 11.A ; 12.B. 二、填空题:本大题共 4 小题,每小题 5 分,共 20 分. 13. 1 8 ;14. 3 (或写成 60 );15. 20 , 3 30 2 (或写成 3 13500 );16.3 . 三、解答题:共 70 分。解答应写出文字说明,证明过程或演算步骤。 17.(12 分) (1)证明: PAD 为等边三角形, E 为 AD 的中点, PE AD∴ 平面 PAD 底面 ABCD,平面 PAD 底面 =ABCD AD PE ∴ 底面 , BC 平面 , PE BC∴ „„„„„3 分 由又题意可知 ABCE 为正方形, CE BC ,又 PE EC E , BC 平面 PCE „„„„„„„„„„„„„„„„„„5 分 平面 PBC , 平面 PBC 平面 PCE „„„„„„„„„„6 分 (2)解:过 F 作 FG AB ,垂足为G „„„„„„„„„„„„„„„„„„8 分 1 1 1 1 1 8 4 3133 3 2 3 2 5 15F ABP P ABF ABFV V S PE AB FG PE „„„„„„„„„„„„„„„„„„„„„„„„„„„„„„12 分 文科数学答案 第 2 页 共 2 页 18.(12 分) 解:(1) 由题设及正弦定理得 sin sin sin cos 3sin sinB C A B A B A B C sin sin( )C A B sin sin( ) sin cos 3 sin sinB A B A B A B „„„„„„„„„„„2 分 化简得 sin ( 3 sin cos 1) 0B A A „„„„„„„„„„„„„4 分 sin 0B , 3sin cos 1AA, 1sin 62A 0 A , 3A „„„„„„„„„„„„„„„„„„6 分 (2)由已知 23a (1),根据余弦定理得 2212cos 2 bcA bc ,即 221 12 22 bc bc , 22= 12bc b c „„„„„„„„„„„„8 分 222 , 12b c bc bc (当且仅当 =bc时取号) „„„„„„„„„10 分 1 1 3 1 3sin 12 3 32 2 2 2 2ABCS bc A bc „„„„„„„„12 分 (当且仅当 时取号) 19. (12 分) 解:(1) =30 =20, =50, =50m n x y, „„„„„„„„„„„„3 分 (2) 2 2 50 100(20 20 30 30) 50 =4 1050 .82850K ,没有99.9% 把握认为新冠肺炎的 感染程度和性别有关. „„„„„„„„„„„„„„„„„„„„„7 分 文科数学答案 第 3 页 共 3 页 (3)由于在“轻-中度感染”的患者中,按男女比例为 2:3,设抽取的 5 人中 3 名 女性患者用 ,,abc表示,2 名男性患者用 ,DE表示,则所有组合为( , , )D E a , ( , , )D E b ,( , , )D E c ,( , , )D a b ,( , , )D a c ,( , , )D b c ,( , , )E a b ,( , , )E a c ,( , , )E b c , ( , , )abc ,可能的情况共有 10 种.其中至少抽到 2 名女性患者的情况有 7 种,设 至少抽到 2 名女性患者的事件为 A ,则 7()10PA= .„„„„„„„„„„12 分 20.(12 分) 解:(1)由已知得动点 M 到点 )1,0(F 的距离与到直线 1: yl 的距离相等„2 分 又由抛物线的定义可知,曲线 C 为抛物线,焦点为 ,准线为 曲线C 的方程为 2 4xy „„„„„„„„„„„„„„„5 分 (2)设点 11( , )A x y , 22( , )B x y , )1,( tP „„„„„„„„„„„„„„6 分 由 2 4xy ,即 21 4yx, 得 y 1 2 x . ∴抛物线C 在点 A 处的切线 PA 的方程为 )(2 1 1 1 xxxyy 即 2 11 1 2 1 2 xyxxy . „„„„„„„„„„„„„„„„„8 分 ∵ 2 11 4 1 xy , ∴ 1 1 2 yxxy ,∵点 在切线 PA 上, ∴ 1 1 21 ytx ①,同理 2 2 21 ytx ② „„„„„„„„„„„10 分 综合①、②得,点 1 1 2 2( , ), ( , )A x y B x y 的坐标都满足方程 ytx 21 即直线 :AB 12 xty 恒过抛物线焦点 F )1,0( „„„„„„„„„12 分 文科数学答案 第 4 页 共 4 页 21.(12 分) 解:(1)函数 ()fx的定义域为(0 + ), . 1 ( 1)( 1)( ) (1 ) = x axf x ax a xx „„„„„„„„„„„„„„„2 分 0, 0ax , 012 x ax , 100' xxf ,函数 xf 在(0,1) 上为减函数; 10' xxf ,函数 在(1, ) 上为增函数 所以, 211 afxf 极小值 ,无极大值 „„„„„„„„„„„„5 分 (2)由(1)可得 011' xx xaxxf 0a ,由 0' xf ,可得 1,1 21 xax „„„„„„„„„„„„6 分 当 11- a ,即 01- a 时, 0' xf 在 1,4 1x 成立, xf 在此区间 1,4 1 上 为减函数,所以, 211min afxf „„„„„„„„„„„„„„7 分 当 11-4 1 a ,即 14 a 时, 0,1,1;0,1,4 1 '' xfaxxfax 所以, xf 在 a 1,4 1 为减函数,在 1,1 a 为增函数 所以, aaafxf 1ln2 111 min „„„„„„„„„„„„„9 分 当 4 11-0 a ,即 4a 时, 0,1,4 1 ' xfx , xf 在 1,4 1x 为增 函数 2ln232 7 4 1 4 1 min afxf „„„„„„„„„„„„„11 分 文科数学答案 第 5 页 共 5 页 综上所述, 01,21 14,1ln2 11 4,2ln232 7-4 1 min aa aaa aa xf „„„„„„„„„„12 分 22.(10 分)选修 4-4:坐标系与参数方程 解:(1) 2 2 2 2 2 12 , 3 sin 12.3 sin 由 cos sin x y 得 223 4 12,xy 曲线C 的直角坐标方程为 22 143 xy. 当 2a 时,直线l 的普通方程为 2 2 0xy „„„„„„„„„„3 分 由 22 2 2 0 143 xy xy 解得 2 0 x y 或 1 3 2 x y . 从而 与 的交点坐标为 32,0 , 1, 2 .„„„„„„„„„„„„„„5 分 (2)由题意知直线 的普通方程为 20x y a , 的参数方程为 2cos 3 sin x y ( 为参数) 故 上任意一点 2cos , 3 sinP 到 的距离为 4sin2cos 2 3sin 6 55 aa d „„„„„„„„„„8 分 则 2 4sin 62sin 45 5 adPA d . 文科数学答案 第 6 页 共 6 页 当 0a 时, PA 的最大值为 24 10 5 a ,所以 1a ; 当 0a 时, 的最大值为 24 10 5 a ,所以 1a . 综上所述, 或 „„„„„„„„„„„„„„„„„„„„„„10 分 23.(10 分)选修 4-5:不等式选讲 (1)解: 3, 1 ( ) 2 1, 1 2 3, 2 x f x x x x „„„„„„„„„„„„„„„„„„3 分 当 1x 时, 31恒成立,所 ; 当 12x 时, 2 1 1x即 1x ,所 11x ; 当 2x 时,31 显然不成立,所以不合题意; 综上所述,不等式的解集为 ( ,1] „„„„„„„„„„„„„„„„5 分 (2)证明:由(1)知 max( ) 3f x s,于是 3abc 由基本不等式可得 2 2 2 2 2 4 2 222a b b c a b c ab c (当且仅当 ac 时取等号) 2 2 2 2 2 2 4 222b c c a a b c abc (当且仅当ba 时取等号) 2 2 2 2 4 2 2 222c a a b a b c a bc (当且仅当cb 时取等号)„„„„„„8 分 上述三式相加可得 2 2 2 2 2 22( ) 2 ( )a b b c c a abc a b c (当且仅当 abc时取等号) 3abc , 2 2 2 2 2 2 3a b b c c a abc ,故得证„„„„„„„„10 分查看更多