- 2021-04-20 发布 |
- 37.5 KB |
- 4页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
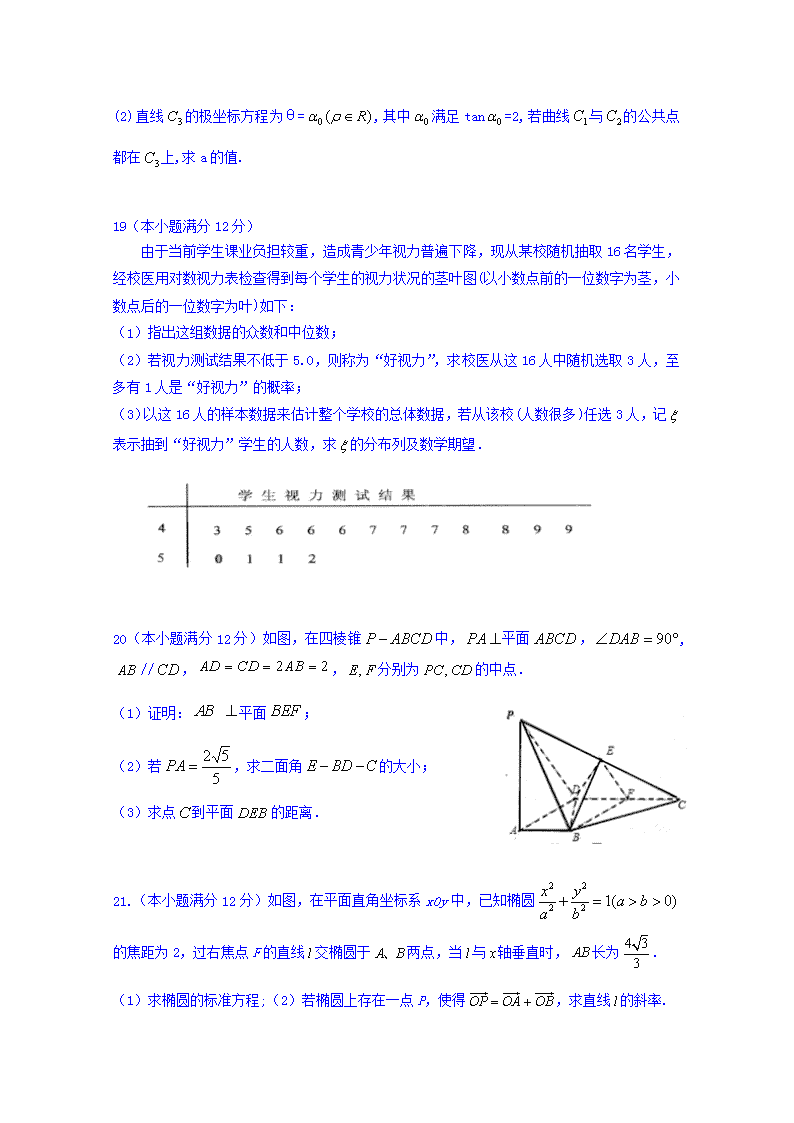
2017-2018学年湖南省张家界市民族中学高二下学期第一次月考数学(理)试题 缺答案
2017-2018学年湖南省张家界市民族中学高二下学期第一次月考理科数学试题 时量:90分钟 满分:100分 一、选择题(每小题5分,共60分) 1.复数的虚部是( ) A. B. C. D. 2.在极坐标系中,方程表示的曲线是( ) A.直线 B双曲线. C.椭圆 D.圆 3 函数,则等于( ) A. B. C. D. 4.用反证法证明命题“三角形的内角中至少有一个角不大于60°”时,应假设( ) A.三角形的三个内角都不大于60° B.三角形的三个内角都大于60° C.三角形的三个内角至多有一个大于60° D.三角形的三个内角至少有两个大于60° 5.命题“∀x∈R,使得n≥x2”的否定形式是( ) A.∀x∈R,使得n<x2 B.∃x∈R,使得n≥x2 C.∃x∈R, 使得n<x2 D.∀x∈R,使得n≤x2 6若 的展开式中的第5项为常数,则n为( ) A.8 B.10 C.12 D.15 7.由直线,曲线及轴所围图形的面积为 ( ) A.3 B.7 C. D. 8. 某外商计划在5个候选城市投资3个不同的项目,且在同一个城市投资的项目不超过2个,则该外商不同的投资方案有( ) A.60种 B.70种 C.80种 D.120种 9.袋中装有大小相同的5只球,上面分别标有1,2,3,4,5,在有放回的条件下依次取出两球,设两球号码之和为随机变量X,则X所有可能值的个数是( ) A.25 B.10 C.9 D.5 10.数学归纳法证明(n+1)•(n+2)•…•(n+n)=2n×1×3×…×(2n﹣1)(n∈N*)成立时,从n=k到n=k+1左边需增加的乘积因式是( ) A. 2(2k+1) B. C. 2k+1 D. 11. 将曲线y=sin 2x按照伸缩变换后得到的曲线方程为( ) A.y′=3sin x′ B.y′=3sin 2x′ C.y′=3sinx′ D.y′=sin 2x′ 12.若函数的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称具有性质.下列函数中具有性质的是( ) A. B. C. D. 二、填空题(每小题5分,共20分) 13.若直线(t为参数)与曲线(θ为参数,a>0)有且只有一个公共点,则a=_________ 14.= ________ 15.甲、乙两队进行排球决赛.现在的情形是甲队只要再赢一局就获冠军,乙队需要再赢两局才能得冠军.若两队胜每局的概率相同,则甲队获得冠军的概率为________ 16.设,若,则实数=________. 三、解答题(共6个小题,共70分) 17.(本题满分10分) 已知集合A={ |},B={|},若x∈A是x∈B的必要不充分条件,求实数的取值范围. 18(本题满分12分)在直线坐标系xOy中,曲线的参数方程为 (t为参数, a>0).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线:ρ=4cosθ. (1)说明是哪一种曲线,并将的方程化为极坐标方程; (2)直线的极坐标方程为θ=,其中满足tan=2,若曲线与的公共点都在上,求a的值. 19(本小题满分12分) 由于当前学生课业负担较重,造成青少年视力普遍下降,现从某校随机抽取16名学生,经校医用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如下: (1)指出这组数据的众数和中位数; (2)若视力测试结果不低于5.0,则称为“好视力”,求校医从这16人中随机选取3人,至多有1人是“好视力”的概率; (3)以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记表示抽到“好视力”学生的人数,求的分布列及数学期望. 20(本小题满分12分)如图,在四棱锥中,平面,,//,,分别为的中点. (1) 证明: 平面; (2)若,求二面角的大小; (3)求点到平面的距离. 21.(本小题满分12分)如图,在平面直角坐标系xOy中,已知椭圆的焦距为2,过右焦点F的直线交椭圆于两点,当与轴垂直时,长为. (1)求椭圆的标准方程;(2)若椭圆上存在一点P,使得,求直线的斜率. 22(本题满分12分)已知函数, . (1)若函数在处取得极小值0,求的值; (2)在(Ⅰ)的条件下,求证:对任意,总有; (3)求函数的单调递增区间.查看更多