- 2021-04-20 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020八年级数学上册 单元清六 (新版)浙教版
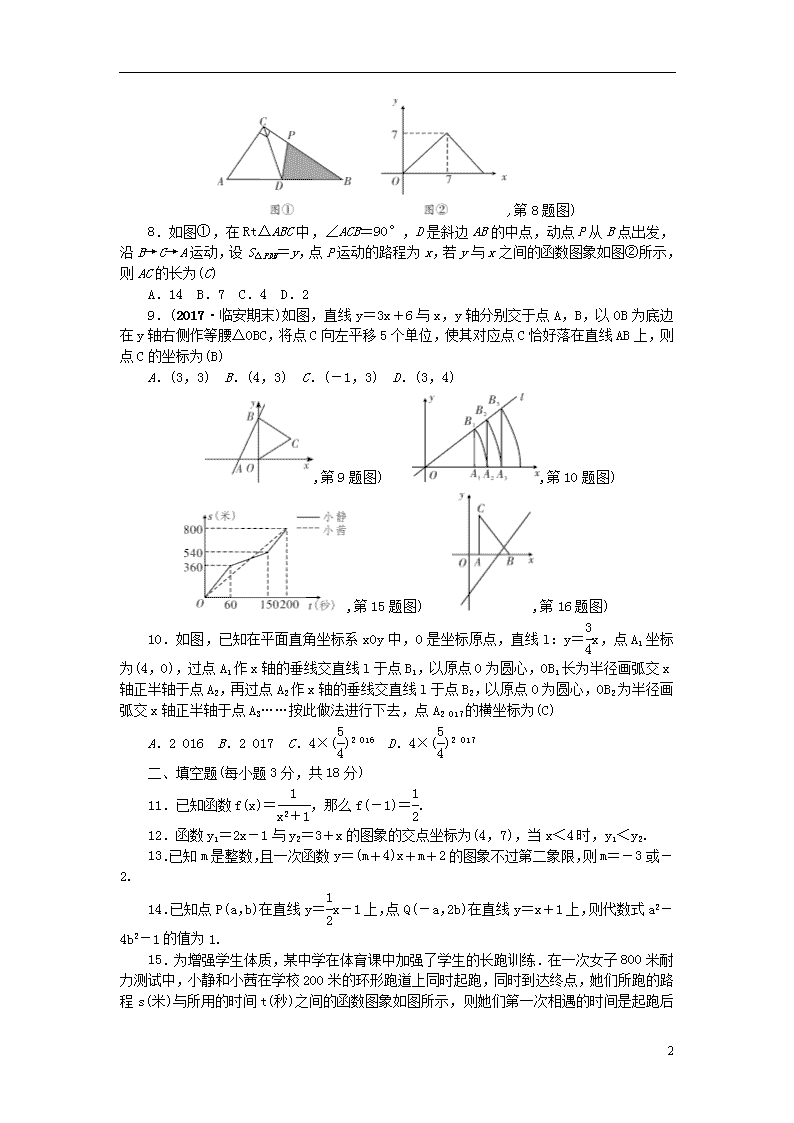
检测内容:第5章 一次函数 得分________ 卷后分________ 评价________ 一、选择题(每小题3分,共30分) 1.函数y=的自变量x的取值范围是(C) A.x≠-1 B.x≠2 C.x≠±2 D.x≠-2 2.若正比例函数y=(1-4m)x的图象经过点A(x1,y1)和点B(x2,y2),且当x1<x2时,y1>y2,则m的取值范围是(D) A.m<0 B.m>0 C.m< D.m> 3.已知一次函数y=kx+b的图象经过点(0,-3)和点(1,5),则这个一次函数的表达式是(A) A.y=8x-3 B.y=-8x-3 C.y=8x+3 D.y=-8x+3 4.已知直线l1:y=-3x+b与直线l2:y=-kx+1在同一坐标系中的图象交于点(1,-2),那么方程组的解是(A) A. B. C. D. 5.小明早上从家中出发到离家1.2 km的早餐店吃早餐,他用了一刻钟吃完早餐后按原路返回到离家1 km的学校上课,下列能反映这一过程的大致图象是(B) 6.若直线y=x-2与直线y=x+a的交点在x轴上,则直线y=x+a不经过(B) A.第一象限 B.第二象限 C.第三象限 D.第四象限 7.已知A,B两地相距120千米,甲乙两人沿同一条公路匀速行驶,甲骑自行车以20千米/时从A地前往B地,同时乙骑摩托车从B地前往A地,设两人之间的距离为s(千米),甲行驶的时间为t(小时),若s与t的函数关系如图所示,则下列说法错误的是(B) A.经过2小时两人相遇 B.若乙行驶的路程是甲的2倍,则t=3 C.当乙到达终点时,甲离终点还有60千米 D.若两人相距90千米,则t=0.5或t=4.5 ,第7题图) 7 ,第8题图) 8.如图①,在Rt△ABC中,∠ACB=90°,D是斜边AB的中点,动点P从B点出发,沿B→C→A运动,设S△PDB=y,点P运动的路程为x,若y与x之间的函数图象如图②所示,则AC的长为(C) A.14 B.7 C.4 D.2 9.(2017·临安期末)如图,直线y=3x+6与x,y轴分别交于点A,B,以OB为底边在y轴右侧作等腰△OBC,将点C向左平移5个单位,使其对应点C恰好落在直线AB上,则点C的坐标为(B) A.(3,3) B.(4,3) C.(-1,3) D.(3,4) ,第9题图) ,第10题图) ,第15题图) ,第16题图) 10.如图,已知在平面直角坐标系xOy中,O是坐标原点,直线l:y=x,点A1坐标为(4,0),过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴正半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2为半径画弧交x轴正半轴于点A3……按此做法进行下去,点A2 017的横坐标为(C) A.2 016 B.2 017 C.4×()2 016 D.4×()2 017 二、填空题(每小题3分,共18分) 11.已知函数f(x)=,那么f(-1)=. 12.函数y1=2x-1与y2=3+x的图象的交点坐标为(4,7),当x<4时,y1<y2. 13.已知m是整数,且一次函数y=(m+4)x+m+2的图象不过第二象限,则m=-3或-2. 14.已知点P(a,b)在直线y=x-1上,点Q(-a,2b)在直线y=x+1上,则代数式a2-4b2-1的值为1. 15.为增强学生体质,某中学在体育课中加强了学生的长跑训练.在一次女子800米耐力测试中,小静和小茜在学校200米的环形跑道上同时起跑,同时到达终点,她们所跑的路程s(米)与所用的时间t(秒)之间的函数图象如图所示,则 7 她们第一次相遇的时间是起跑后的第120秒. 16.如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0),将△ABC沿x轴向右平移,当点C落在直线y=x-4上时,线段BC扫过的面积为20. 三、解答题(共72分) 17.(8分)已知一次函数y=kx+4(k≠0). (1)当x=-1,y=2,求此函数的表达式; (2)函数图象与x轴,y轴的交点分别为A,B,求出△AOB的面积; (3)利用图象求出当y≤3时,x的取值范围. 解:(1)∵当x=-1时,y=2,∴2=-k+4,得k=2,∴此函数的表达式为y=2x+4. (2)当x=0时,y=4;当y=0时,x=-2,∴点A的坐标为(-2,0),点B的坐标为(0,4),∴△AOB的面积是=4. (3)y≤3时,2x+4≤3,得x≤-0.5,即x的取值范围是x≤-0.5.图象略. 18.(8分)已知函数y=-2x+6与函数y=3x-4. (1)在同一平面直角坐标系内,画出这两个函数的图象; (2)求这两个函数图象的交点坐标; (3)根据图象回答,当x在什么范围内取值时,函数y=-2x+6的图象在函数y=3x-4的图象的上方? 解:(1)函数y=-2x+6的图象与坐标轴的交点为(0,6),(3,0);函数y=3x-4的图象与坐标轴的交点为(0,-4),,函数图象略. (2)(2,2). (3)由图象知,当x<2时,函数y=-2x+6的图象在函数y=3x-4的图象的上方. 19.(8分)如图,一次函数y=x+2的函数图象与x轴,y轴分别交于点A,B. (1)若点P(-1,m)为第三象限内一个动点,请问△OPB的面积会变化吗?若不变, 7 请求出面积;若变化,请说明理由; (2)在(1)的条件下,试用含m的代数式表示四边形APOB的面积;若△APB的面积是4,求m的值. 解:(1)不变.∵一次函数y=x+2的函数图象与x轴,y轴分别交于点A,B,∴A(-2,0),B(0,2),∴OB=2.∵P(-1,m),∴S△OPB=OB×1=×2×1=1. (2)∵A(-2,0),P(-1,m),∴S四边形APOB=S△AOP+S△AOB=OA·(-m)+OA×2=-×2m+×2×2=2-m.∵S四边形APOB=S△APB+S△OPB=4+1=5,∴2-m=5,解得m=-3. 20.(8分)(2018·长春模拟)某汽车租赁公司对某款汽车的租赁方式按时段计算,该公司要求租赁方必须在9天内(包括9天)将所租汽车归还,租赁费用y(元)随时间x(天)的变化图象为折线OA-AB-BC,如图所示. (1)当租赁时间不超过3天时,每日租金为150元; (2)当6≤x≤9时,y与x的函数表达式为y=210x-450(6≤x≤9); (3)甲、乙两人租赁该款汽车各一辆,两人租赁时间一共为9天,甲租的天数少于3天,乙比甲多支付费用720元.请问乙租这款汽车多长时间? 解:(2)点拨:设BC的表达式为y=kx+b,由函数图象,得解得∴y与x之间的函数表达式为y=210x-450(6≤x≤9). (3)设乙租这款车a(6查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档