2018届二轮复习2-4幂函数与二次函数课件(全国通用)
2
.
4
幂函数与二次函数
-
2
-
-
3
-
知识梳理
考点自测
1
.
幂函数
(1)
幂函数的定义
:
形如
(
α
∈
R
)
的函数称为幂函数
,
其中
x
是
,
α
是
.
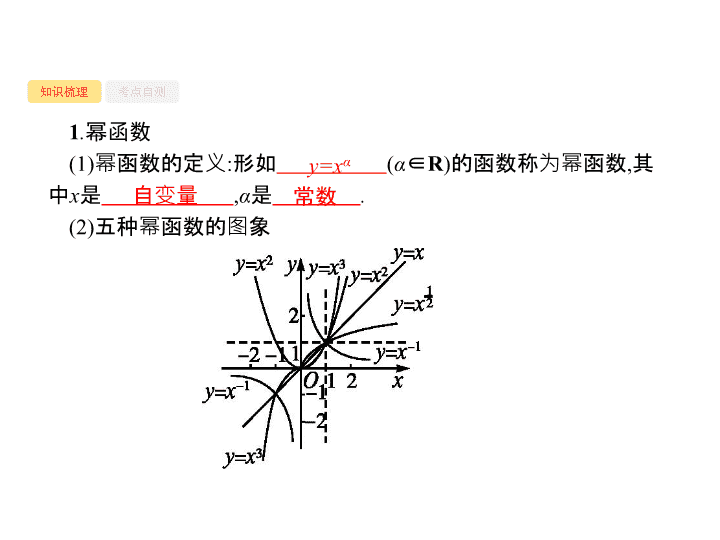
(2)
五种幂函数的图象
y=x
α
自变量
常数
-
4
-
知识梳理
考点自测
(3)
五种幂函数的性质
R
R
R
[0,
+∞
)
{
x|x
∈
R
,
且
x
≠0}
R
[0,
+∞
)
R
[0,
+∞
)
{
y|y
∈
R
,
且
y
≠0}
增
x
∈
[0,
+∞
)
时
,
增
,
x
∈
(
-∞
,0)
时
,
减
增
增
x
∈
(0,
+∞
)
时
,
减
,
x
∈
(
-∞
,0)
时
,
减
-
5
-
知识梳理
考点自测
2
.
二次函数
(1)
二次函数的三种形式
一般式
:
;
顶点式
:
,
其中
为顶点坐标
;
零点式
:
,
其中
为二次函数的零点
.
f
(
x
)
=ax
2
+bx+c
(
a
≠0)
f
(
x
)
=a
(
x-h
)
2
+k
(
a
≠0)
(
h
,
k
)
f
(
x
)
=a
(
x-x
1
)(
x-x
2
)(
a
≠0)
x
1
,
x
2
-
6
-
知识梳理
考点自测
(2)
二次函数的图象和性质
-
7
-
知识梳理
考点自测
-
8
-
知识梳理
考点自测
1
.
幂函数
y=x
α
在第一象限的两个重要结论
:
(1)
恒过点
(1,1);
(2)
当
x
∈
(0,1)
时
,
α
越大
,
函数值越小
;
当
x
∈
(1,
+∞
)
时
,
α
越大
,
函数值越大
.
-
9
-
知识梳理
考点自测
-
10
-
知识梳理
考点自测
×
×
×
√
√
-
11
-
知识梳理
考点自测
2
.
(
教材习题改编
P
39
A
组
T
1(1)
)
已知函数
y=x
2
+ax+
6
在
内是增函数
,
则
a
的取值范围为
(
)
A.
a
≤
-
5 B.
a
≤
5
C.
a
≥
-
5 D.
a
≥
5
C
3
.
如图是
①
y=x
a
;
②
y=x
b
;
③
y=x
c
在第一象限的图象
,
则
a
,
b
,
c
的大小关系为
(
)
A.
a>b>c
B.
a
0
时
,
幂函数的图象经过点
(1,1)
和
(0,0),
且在
(0,
+∞
)
内单调递增
.
(3)
当
α
<
0
时
,
幂函数的图象经过点
(1,1),
且在
(0,
+∞
)
内单调递减
.
(4)
幂函数图象在第一象限的特点
:
当
α
>
1
时
,
曲线下凸
;
当
0
<
α
<
1
时
,
曲线上凸
;
当
α
<
0
时
,
曲线下凸
.
-
16
-
考点一
考点二
考点三
a>c>b
-
17
-
考点一
考点二
考点三
求二次函数的解析式
例
2
已知二次函数
f
(
x
)
满足
f
(2)
=-
1,
f
(
-
1)
=-
1,
且
f
(
x
)
的最大值是
8,
求
f
(
x
)
的解析式
.
-
18
-
考点一
考点二
考点三
-
19
-
考点一
考点二
考点三
思考
求二次函数的解析式时如何选取恰当的表达形式
?
解题心得
根据已知条件确定二次函数的解析式
,
一般用待定系数法
,
选择规律如下
:
(1)
已知三个点的坐标
,
宜选用一般式
.
(2)
已知顶点坐标、对称轴、最大
(
小
)
值等
,
宜选用顶点式
.
(3)
已知图象与
x
轴的两个交点坐标
,
宜选用交点式
.
-
20
-
考点一
考点二
考点三
对点训练
2
已知二次函数
f
(
x
)
有两个零点
0
和
-
2,
且它有最小值
-
1,
则
f
(
x
)
的解析式为
.
f
(
x
)
=x
2
+
2
x
解析
:
因为
f
(
x
)
有两个零点
0
和
-
2,
所以可设
f
(
x
)
=ax
(
x+
2)(
a
≠0),
此时
f
(
x
)
=ax
(
x+
2)
=a
(
x+
1)
2
-a.
因为
f
(
x
)
有最小值
-
1,
因此
f
(
x
)
的解析式是
f
(
x
)
=x
(
x+
2)
=x
2
+
2
x.
-
21
-
考点一
考点二
考点三
二次函数的图象与性质
(
多考向
)
考向
1
二次函数在闭区间上的最值问题
例
3
(1)
已知函数
f
(
x
)
=-x
2
+
2
ax+
1
-a
在区间
[0,1]
上有最大值
2,
则
a
的值为
;
(2)
若函数
y=x
2
-
2
x+
3
在区间
[0,
m
]
上有最大值
3,
最小值
2,
则
m
的取值范围为
.
-
1
或
2
[1,2]
-
22
-
考点一
考点二
考点三
解析
:
(1)
函数
f
(
x
)
=-x
2
+
2
ax+
1
-a=-
(
x-a
)
2
+a
2
-a+
1,
对称轴方程为
x=a.
当
a<
0
时
,
f
(
x
)
max
=f
(0)
=
1
-a
,
则
1
-a=
2,
即
a=-
1
.
当
0
≤
a
≤
1
时
,
f
(
x
)
max
=a
2
-a+
1,
则
a
2
-a+
1
=
2,
即
a
2
-a-
1
=
0,
解得
(
舍去
)
.
当
a>
1
时
,
f
(
x
)
max
=f
(1)
=a
,
则
a=
2
.
综上可知
,
a=-
1
或
a=
2
.
(2)
作出函数
y=x
2
-
2
x+
3
的图象如图所示
.
由图象可知
,
要使函数在区间
[0,
m
]
上取得最小值
2,
则
1
∈
[0,
m
],
从而
m
≥
1
.
当
x=
0
时
,
y=
3;
当
x=
2
时
,
y=
3,
所以要使函数取得最大值为
3,
则
m
≤
2
.
故所求
m
的取值范围为
[1,2]
.
思考
如何求二次函数在含参数的闭区间上的最值
?
-
23
-
考点一
考点二
考点三
考向
2
与二次函数有关的存在性问题
例
4
已知函数
f
(
x
)
=x
2
-
2
x
,
g
(
x
)
=ax+
2(
a>
0),
对任意的
x
1
∈
[
-
1,2]
都存在
x
0
∈
[
-
1,2],
使得
g
(
x
1
)
=f
(
x
0
),
则实数
a
的取值范围是
.
-
24
-
考点一
考点二
考点三
思考
如何理解本例中对任意的
x
1
∈
[
-
1,2]
都存在
x
0
∈
[
-
1,2],
使得
g
(
x
1
)
=f
(
x
0
)?
-
25
-
考点一
考点二
考点三
考向
3
与二次函数有关的恒成立问题
例
5
(1)
已知函数
f
(
x
)
=x
2
+mx-
1,
若对于任意
x
∈
[
m
,
m+
1],
都有
f
(
x
)
<
0
成立
,
则实数
m
的取值范围是
;
(2)
已知函数
f
(
x
)
=x
2
+
2
x+
1,
f
(
x
)
>x+k
在区间
[
-
3,
-
1]
上恒成立
,
则
k
的取值范围为
.
(
-∞
,1)
-
26
-
考点一
考点二
考点三
解析
:
(1)
作出二次函数
f
(
x
)
的草图
,
对于任意
x
∈
[
m
,
m+
1],
都有
f
(
x
)
<
0,
(2)
由题意得
x
2
+x+
1
>k
在区间
[
-
3,
-
1]
上恒成立
.
设
g
(
x
)
=x
2
+x+
1,
x
∈
[
-
3,
-
1],
则
g
(
x
)
在
[
-
3,
-
1]
上递减
.
∴
g
(
x
)
min
=g
(
-
1)
=
1
.
∴
k<
1
.
故
k
的取值范围为
(
-∞
,1)
.
思考
由不等式恒成立求参数取值范围的解题思路是什么
?
-
27
-
考点一
考点二
考点三
考向
4
与二次函数有关的零点分布问题
例
6
已知方程
x
2
+
(
k-
2)
x+
2
k-
1
=
0
的两根中
,
一根在
0
和
1
之间
,
另一根在
1
和
2
之间
,
则实数
k
的取值范围是
.
思考
已知与二次函数有关的零点分布
,
如何求参数的取值范围
?
-
28
-
考点一
考点二
考点三
解题心得
1
.
二次函数在闭区间上的最值主要有三种类型
:
轴定区间定、轴动区间定、轴定区间动
,
不论哪种类型
,
解决的关键是考虑对称轴与区间的关系
,
当含有参数时
,
要依据对称轴与区间的关系进行分类讨论
,
当确定了对称轴和区间的关系
,
就明确了函数的单调性
,
从而确定函数的最值
.
-
29
-
考点一
考点二
考点三
3
.
由不等式恒成立求参数取值范围的思路及关键
:
(1)
一般有两种解题思路
:
一是分离参数
,
将问题归结为求函数的最值
;
二是不分离参数
,
通常结合函数图象寻求使不等式恒成立的条件
.
(2)
两种思路都比较简便
,
至于用哪种方法
,
关键是看参数是否已分离
.
4
.
已知与二次函数有关的零点分布求参数的取值范围
,
主要采取数形结合的方法
,
通过二次函数的图象的开口方向、对称轴、特殊点对应的函数值等列出满足题意的不等式
,
解不等式得参数的取值范围
.
-
30
-
考点一
考点二
考点三
对点训练
3
(1)
若函数
f
(
x
)
=x
2
-ax-a
在
[0,2]
上的最大值为
1,
则实数
a
等于
(
)
A.
-
1 B.1 C.
-
2 D.2
(2)
已知
a
是实数
,
函数
f
(
x
)
=
2
ax
2
+
2
x-
3
在
[
-
1,1]
上的值恒小于零
,
则
a
的取值范围为
;
(3)
已知
f
(
x
)
=x
2
-
2
x+
4,
g
(
x
)
=a
x
(
a>
0,
且
a
≠0),
若对任意的
x
1
∈
[1,2]
都存在
x
2
∈
[
-
1,2],
使得
f
(
x
1
)
0,
f
(1)
<
0
或
a<
0,
f
(1)
>
0
.
当
a>
0
时
,
由
f
(1)
=a+
(
a+
1)
+a
2
-
4
<
0,
得
0
0,
得
a<-
3
.
综上所述
,
实数
a
的取值范围是
(
-∞
,
-
3)
∪
(0,1)
.
-
34
-
考点一
考点二
考点三
1
.
幂函数
y=x
α
(
α
∈
R
)
的图象的特征
:
当
α>
0
时
,
图象过原点和点
(1,1),
在第一象限内从左到右图象逐渐上升
;
当
α
<
0
时
,
图象过点
(1,1),
但不过原点
,
在第一象限内从左到右图象逐渐下降
.
2
.
求二次函数的解析式时
,
应根据题目给出的条件
,
选择恰当的表示形式
.
3
.
“
恒成立
”
与
“
存在性
”
问题的求解是
“
互补
”
关系
,
即
f
(
x
)
≥
g
(
a
)
对于
x
∈
D
恒成立
,
应求
f
(
x
)
的最小值
;
若存在
x
∈
D
,
使得
f
(
x
)
≥
g
(
a
)
成立
,
应求
f
(
x
)
的最大值
.
-
35
-
考点一
考点二
考点三
1
.
幂函数的图象一定会出现在第一象限
,
一定不会出现在第四象限
.
如果幂函数与坐标轴有交点
,
那么交点一定是原点
.
2
.
对于函数
y=ax
2
+bx+c
,
若它是二次函数
,
则必须满足
a
≠0
.
当题目条件中未说明
a
≠0
时
,
就要分
a=
0
和
a
≠0
两种情况讨论
.