- 2021-04-20 发布 |
- 37.5 KB |
- 33页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高考物理考点46 洛伦兹力 带电粒子在磁场中的运动
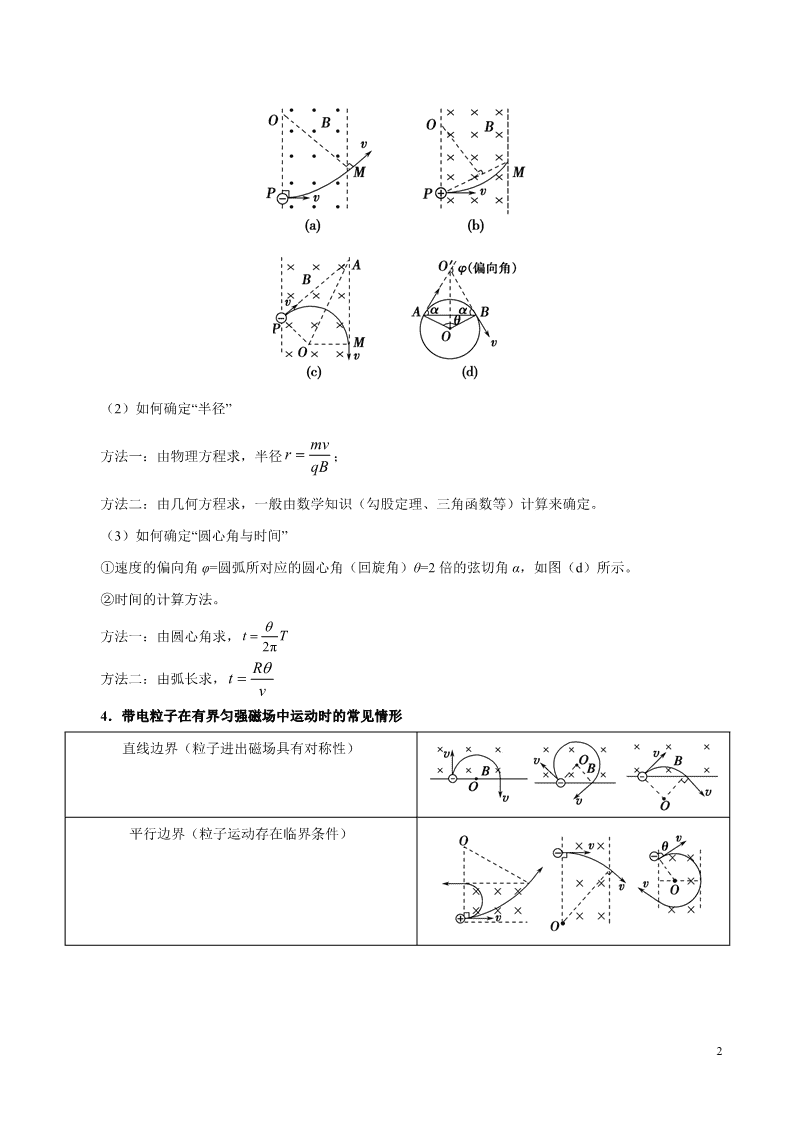
1 考点 46 洛伦兹力 带点粒子在磁场中的运动 1.洛伦兹力与电场力的比较 洛伦兹力 电场力 性质 磁场对在其中运动的电荷的作用力 电场对放入其中电荷的作用力 产生条件 v≠0 且 v 不与 B 平行 电场中的电荷一定受到电场力作用 大小 F=qvB(v⊥B) F=qE 力方向与场方向的关系 一定是 F⊥B,F⊥v,与电荷电性无关 正电荷受力与电场方向相同,负电荷受 力与电场方向相反 做功情况 任何情况下都不做功 可能做正功、负功,也可能不做功 力为零时场的情况 F 为零,B 不一定为零 F 为零,E 一定为零 作用效果 只改变电荷运动的速度方向,不改变速 度大小 既可以改变电荷运动的速度大小,也可 以改变电荷运动的方向 2.洛伦兹力与安培力的联系及区别 (1)安培力是洛伦兹力的宏观表现,二者是相同性质的力,都是磁场力。 (2)洛伦兹力对电荷不做功;安培力对通电导线可做正功,可做负功,也可不做功。[来源:ZXXK] 3.带电粒子在匀强磁场中的运动 (1)如何确定“圆心” ①由两点和两线确定圆心,画出带电粒子在匀强磁场中的运动轨迹。确定带电粒子运动轨迹上的两个 特殊点(一般是射入和射出磁场时的两点),过这两点作带电粒子运动方向的垂线(这两垂线即为粒子在 这两点所受洛伦兹力的方向),则两垂线的交点就是圆心,如图(a)所示。 ②若只已知过其中一个点的粒子运动方向,则除过已知运动方向的该点作垂线外,还要将这两点相连 作弦,再作弦的中垂线,两垂线交点就是圆心,如图(b)所示。 ③若只已知一个点及运动方向,也知另外某时刻的速度方向,但不确定该速度方向所在的点,如图 (c)所示,此时要将其中一速度的延长线与另一速度的反向延长线相交成一角(∠PAM),画出该角的角 平分线,它与已知点的速度的垂线交于一点 O,该点就是圆心。 2 (2)如何确定“半径” 方法一:由物理方程求,半径 ; 方法二:由几何方程求,一般由数学知识(勾股定理、三角函数等)计算来确定。 (3)如何确定“圆心角与时间” ①速度的偏向角 φ=圆弧所对应的圆心角(回旋角)θ=2 倍的弦切角 α,如图(d)所示。 ②时间的计算方法。 方法一:由圆心角求, 方法二:由弧长求, 4.带电粒子在有界匀强磁场中运动时的常见情形 直线边界(粒子进出磁场具有对称性) 平行边界(粒子运动存在临界条件) qB mvr 2πt T v Rt 3 圆形边界(粒子沿径向射入,再沿径向射出) 5.带电粒子在有界磁场中的常用几何关系 (1)四个点:分别是入射点、出射点、轨迹圆心和入射速度直线与出射速度直线的交点。 (2)三个角:速度偏转角、圆心角、弦切角,其中偏转角等于圆心角,也等于弦切角的 2 倍。 6.求解带电粒子在匀强磁场中运动的临界和极值问题的方法 由于带电粒子往往是在有界磁场中运动,粒子在磁场中只运动一段圆弧就飞出磁场边界,其轨迹不是 完整的圆,因此,此类问题往往要根据带电粒子运动的轨迹作相关图去寻找几何关系,分析临界条件(① 带电体在磁场中,离开一个面的临界状态是对这个面的压力为零;②射出或不射出磁场的临界状态是带电 体运动的轨迹与磁场边界相切),然后应用数学知识和相应物理规律分析求解。 (1)两种思路 一是以定理、定律为依据,首先求出所研究问题的一般规律和一般解的形式,然后再分析、讨论临界 条件下的特殊规律和特殊解; 二是直接分析、讨论临界状态,找出临界条件,从而通过临界条件求出临界值。 (2)两种方法 一是物理方法: ①利用临界条件求极值; ②利用问题的边界条件求极值; ③利用矢量图求极值。 二是数学方法: ①利用三角函数求极值; ②利用二次方程的判别式求极值; ③利用不等式的性质求极值; ④利用图象法等。 (3)从关键词中找突破口:许多临界问题,题干中常用“恰好”、“最大”、“至少”、“不相撞”、“不脱离” 等词语对临界状态给以暗示。审题时,一定要抓住这些特定的词语挖掘其隐藏的规律,找出临界条件。 4 一个带电粒子沿垂直于磁场方向射入匀强磁场中,由于沿途空气电离而使粒子的动能逐渐减小,轨迹 如图所示。假设粒子的电荷量不变,下列有关粒子的运动方向和所带电性的判断正确的是 A.粒子由 a 向 b 运动,带正电 B.粒子由 b 向 a 运动,带负电 C.粒子由 b 向 a 运动,带正电 D.粒子由 a 向 b 运动,带负电[来源:+网 Z+X+X+K] 【参考答案】B 【详细解析】由题意可知,带电粒子沿垂直于磁场方向射入匀强磁场,粒子的能量逐渐减小,速度减 小,则由公式 得知,粒子的半径应逐渐减小,由图看出,粒子的运动方向是从 b 到 a。在 b 处,粒 子所受的洛伦兹力指向圆心,即斜向左上方,由左手定则判断可知,该粒子带负电。故选 B。 1.如图所示,两匀强磁场的方向相同,以虚线 MN 为理想边界,磁感应强度分别为 B1、B2,今有一质量为 m、电荷量为 e 的电子从 MN 上的 P 点沿垂直于磁场方向射入匀强磁场 B1 中,其运动轨迹为如图虚线所 示的“心”形图线。则以下说法正确的是 A.电子的运行轨迹为 PDMCNEP B.电子运行一周回到 P 用时为 C.B1=2B2 D.B1=4B2 【答案】AC 【解析】根据左手定则可知:电子从 P 点沿垂直于磁场的方向射入匀强磁场 B1 时,受到的洛伦兹力方 mvr qB 1 2π= mT B e 5 向向上,所以电子的运行轨迹为 PDMCNEP,故 A 正确;电子在整个过程中,在匀强磁场 B1 中运动两 个半圆,即运动一个周期,在匀强磁场 B2 中运动半个周期,所以 ,故 B 错误;由图象可 知,电子在匀强磁场 B1 中运动半径是匀强磁场 B2 中运动半径的一半,根据 可知,B1=2B2,故 D 错误,C 正确。故选 AC。 【名师点睛】本题是带电粒子在磁场中运动的问题,要求同学们能根据左手定则判断洛伦兹力的方向, 能结合几何关系求解,知道半径公式及周期公式,难度适中。 2.(2018·百校联盟高考名师猜题保温金卷)如图所示,空间存在一个垂直于纸面向里的匀强磁场区域,磁 感应强度的大小为 B0,该区域是由一个半径为 R 的半圆和一个长为 2R、宽为 的矩形组成。一个质 量为 m、带电荷量为 q 的带正电的粒子从 AB 的中点 M 垂直于 AB 进入磁场,则下列说法正确的是 A.当粒子的速度 v 满足 时,粒子从 AB 边射出磁场 B.当粒子的速度 v 满足 时,粒子从 BC 边射出磁场 C.当粒子的速度 v 满足 时,粒子离开磁场时的速度方向斜向下 D.当粒子的速度 v 满足 时,粒子离开磁场时的速度方向斜向下 【答案】ABC 【解析】当粒子刚好从B 射出磁场时,粒子的轨道半径为 r1,由几何关系可得: ,由 可得: ,当粒子的速度 v 满足 ,粒子从 AB 边射出磁场,选项 A 正确;当粒子刚好 从 C 射 出 磁 场 时 , 粒 子 的 轨 道 半 径 为 r2 , 由 几 何 关 系 可 得 : , , 由 ,当粒子的速度 v 满足 ,粒子从 BC 边射出磁场,选项 B 正确;当粒子离 开磁场时的速度方向平行于 AB 时,粒子的轨道半径为 r3,由几何关系可得: , 1 2 2π π= m mT B e B e r mv Be 1 2 R 00 2 qB Rv m 0 05 2 8 qB R qB Rvm m 07 1 4 qB Rv m ( ) 05 1 4 qB Rv m ( ) 1 1 2r R 2 0 1 mvqvB r 0 2 qB Rv m 00 2 qB Rv m 2 2 2 2 2 1 4R r R r ( ) 2 5 8r R 2 0 3 mvqvB r 0 05 2 8 qB R qB Rvm m 2 2 2 3 3 1 2r R r R ( ) 6 ,由 可得 ,当粒子的速度 v 满足 ,粒子离 开磁场时的速度方向斜向下,选项 C 正确,D 错误。 【名师点睛】本题考查了粒子在磁场中的运动,应用牛顿第二定律以及几何知识即可正确解题。 利用如图所示装置可以选择一定速度范围内的带电粒子。图中板 MN 上方是磁感应强度大小为 B、方向 垂直纸面向里的匀强磁场,板上有两条宽度分别为 2d 和 d 的缝,两缝近端相距为 L。一群质量为 m、电荷 量为 q,具有不同速度的粒子从宽度为 2d 的缝垂直于板 MN 进入磁场,对于能够从宽度为 d 的缝射出的粒 子,下列说法正确的是 A.粒子带正电 B.射出粒子的最大速度为 C.保持 d 和 L 不变,增大 B,射出粒子的最大速度与最小速度之差 增大 D.保持 d 和 B 不变,增大 L,射出粒子的最大速度与最小速度之差增大 【参考答案】BC 【详细解析】由左手定则可判断粒子带负电,故 A 错误;由题意知:粒子的最大半径 、 粒 子 的 最 小 半 径 , 根 据 , 可 得 、 , 则 ,故可知 BC 正确,D 错误。 1.如图所示,MN 是磁感应强度为 B 的匀强磁场的边界。一质量为 m、电荷量为 q 的粒子在纸面内从 O 点 射入磁场。若粒子速度为 v0,最远能落在边界上的 A 点。下列说法正确的有 3 7 1 4r R( ) 2 0 2 mvqvB r 07 1 4 qB Rv m ( ) 07 1 4 qB Rv m ( ) m dLqB 2 )3( 2 3 max dLr 2min Lr qB mvr m dLqBv 2 )3( max m qBLv 2min m qBdvv 2 3 minmax 7 A.若粒子落在 A 点的左侧,其速度一定小于 v0 B.若粒子落在 A 点的右侧,其速度一定大于 v0 C.若粒子落在 A 点左右两侧 d 的范围内,其速度不可能小于 v0–qBd/2m D.若粒子落在 A 点左右两侧 d 的范围内,其速度不可能大于 v0+qBd/2m 【答案】BD 【解析】粒子速度 垂直MN 边界进入磁场时到边界上的的落点最远,距离为 ,若粒子速度 不与 MN 垂直,落点在 A 点左侧,如图示 A 项错; 若粒子落在 A 点的右侧,其半径一定大于 ,速度一定大于 ,B 项对,若粒子落在 A 点左侧 d 处, 设粒子的最小速度为 ,则 ,得 ,若粒子落在 A 点左侧 d 的范 围内,其速度不可能小于 。若粒子落在 A 点右侧 d 处,设粒子的最小速度为 ,则 ,得 ,若粒子落在 A 点左侧 d 的范围内,其速度不可能小于 ,D 项对,C 错。 【名师点睛】粒子从单边界磁场射入时,射入时速度的方向与磁场边界所夹的角度与射出时速度的方向 与磁场边界所夹的角度是相等的。 0v 022 mvr qB 0mv qB 0v 1v 0 1 2 2 2 2 mv dmv r d qB qB 1 0 2 qBdv v m 0 / 2v qBd m 2v 0 2 2 2 2 2 mv dmv r d qB qB 2 0 2 qBdv v m 0 / 2v qBd m 8 2.(2018·湖北省襄阳市高二期末)如图在 x 轴上方存在垂直于纸面向里的磁感应强度为 B 的匀强磁场, 轴下方存在垂直于纸面向外的磁感应强度为 的匀强磁场。一带负电的粒子质量为 ,电荷量为 q,从 原点 O 以与 x 轴成 角斜向上射入磁场,且在 x 轴上方运动半径为 (不计重力),则下列结 论错误的是 A.粒子经偏转一定能回到原点 O B.粒子完成一次周期性运动的时间为 C.粒子在 轴上方和下方两磁场中运动的半径之比为 D.粒子第二次射入 轴上方磁场时,沿 轴方向前进了 【答案】A 【解析】根据左手定则判断可知,负粒子在第一象限和第四象限所受的洛伦兹力方向不同,粒子在第一 象限沿顺时针方向旋转,而在第四象限沿逆时针方向旋转,轨迹如图所示,不可能回到原点 0,故 A 错 误;负粒子在第一象限轨迹所对应的圆心角为 60°,在第一象限轨迹所对应的圆心角也为 60°,在一个周 期内,粒子做圆周运动的周期为 ,粒子在第一象限运动的时间为 t1= ,同理,在第 四象限粒子做圆周运动的周期为 ,运动的时间为 t2= ,完在成一次周期性运动的 时间为 T′=t1+t2= ,故 B 正确;由 r= 得,粒子圆周运动的半径与 B 成反比,则粒子在 x 轴上方和 下方两磁场中运动的半径之比为 1:2,故 C 正确;画出粒子的运动轨迹,根据几何知识得,粒子第二次 射入 x 轴上方磁场时,沿 x 轴前进距离为 x=R+2R=3R,故 D 正确。 2 B 30 m qB 1: 2 3R 2πmT qB 0 0 60 360 3 mT qB 4 mT qB 0 0 60 2 360 3 mT qB m qB mv qB 9 如图所示,A、B 为一对平行板,板长为 l,两板间距离为 d,板间区域内充满着匀强磁场,磁感应强度 大小为 B,方向垂直纸面向里,一个质量为 m,带电量为+q 的带电粒子以初速度 v0,从 A、B 两板的中间, 沿垂直于磁感线的方向射入磁场。求 v0 在什么范围内,粒子能从磁场内射出? 【参考答案】 或 【详细解析】若带电粒子刚好从平行板左边缘射出,如图所示: 由几何关系得: 由牛顿第二定律得: 解得: 若带电粒子刚好从平行板右边缘射出,如图所示: 由几何关系得: 由牛顿第二定律得: 解得: 0 4v qBd m 2 2 0 ( 4 ) 4 d l qBv md 1 4 dr 2 1 1 1 vqv B m r 1 4 qBdv m 2 2 2 2 2( )2 dr r l 2 2 2 2 vqv B m r 2 2 2 ( 4 ) 4 d l qBv md 10 故当 或 时,粒子可以从磁场内射出。 1.如图所示,竖直平行线 MN、PQ 间距离为 a,其间存在垂直纸面向里的匀强磁场(含边界 PQ),磁感 应强度为 B,MN 上 O 处的粒子源能沿不同方向释放比荷为 q/m 的带负电粒子,速度大小相等、方向均 垂直磁场。粒子间的相互作用及重力不计。设粒子速度方向与射线OM 夹角为 θ,当粒子沿 θ=60°射入时, 恰好垂直 PQ 射出。则 A.从 PQ 边界射出的粒子在磁场中运动的最短时间为 B.沿 θ=120°射入的粒子,在磁场中运动的时间最长 C.粒子的速率为 D.PQ 边界上有粒子射出的长度为 【答案】BD 【解析】粒子在磁场中运动过程中,洛伦兹力充当向心力,运动半径 因为所有粒子 和速度都 相 同 , 故 所 有 粒 子 的 运 动 半 径 都 一 样 , 当 粒 子 沿 θ=60° 射 入 时 , 恰 好 垂 直 PQ 射 出 , 可 得 ,故 ,解得 ,当粒子轨迹与 PQ 边界相切时,轨迹最长,运动时间 最长,此时根据几何知识可得 θ=120°,此时是粒子打在 PQ 边界上的最低的点,故相对 Q 的竖直位移为 ,B 正确,C 错误;由于 v 一定,则弧长最短时,时间最短,根据分析可知当粒子 沿着边界 MN 方向向上射入时最短,此时圆心在 MN 上,θ=30°,所以 ,此时是 0 4v qBd m 2 2 0 ( 4 ) 4 d l qBv md π 3 m qB aqB m 2 3a mvr qB m q 2sin30 ar a 2 mva qB 2aqBv m 1 sin 60 3x r a min π 2π π6 =2π 6 m mt qB qB 11 粒子打在边界 PQ 的最上端,根据几何知识可得该点相对 O 点竖直位移为 ,故 PQ 边界上有粒子射出的长度为 ,A 错误,D 正确。 2.(2018·云南省玉溪市高二期末)如图所示,半径为R 的 1/4 圆形区域内存在着垂直纸面向里的匀强磁场, 磁感应强度为 B,磁场的左边垂直 x 轴放置一线型粒子发射装置,能在 0≤y≤R 的区间内各处沿 x 轴正方 向同时发射出速度相同、带正电的同种粒子,粒子质量为 m,电荷量为 q,不计粒子的重力及粒子间的 相互作用力,若某时刻粒子被装置发射出后,经过磁场偏转击中 y 轴上的同一位置,则下列说法中正确 的是 A.粒子都击中在 O 点处 B.粒子的初速度为 C.粒子在磁场中运动的最长时间为 D.粒子到达 y 轴上的最大时间差为 【答案】D 【解析】由题意,某时刻发出的粒子都击中的点是 y 轴上同一点,由最高点射出的只能击中(0,R),则 击中的同一点就是(0,R),A 错误;从最低点射出的也击中(0,R),那么粒子做匀速圆周运动的半径为 R,由洛伦兹力提供向心力得 ,则速度 ,B 错误;偏转角最大的时间最长,显然从最 低点射出的粒子偏转 90°,时间最长,时间 ,C 错误;从最高点直接射向(0,R)的 粒子时间最短,则最长与最短的时间差为 ,D 正确。 【名师点睛】看起来情况比较复杂,但涉及的问题却是常规问题,本题的关键点是粒子源发出的粒子是 速度大小和方向均相同,则其做匀速圆周运动的半径相同,在从最低点的特殊情况就能知道相同的半径 就是圆弧的半径,再结合周期公式能求出最长和最短时间。 2 sin 60 3x r a 1 2 2 3l x x a 2 BqR m m qB π 2 m m qB qB 2vqvB m R BqRv m 1 1 2π π 4 4 2 m mt T qB qB πΔ 2 R m mt t v qB qB 12 (2018·江苏省天一中学高考考前热身卷)如图所示,以直角三角形 AOC 为边界的有界匀强磁场区域, 磁感应强度为 B,∠A=60°, AO=L,在 O 点放置一个粒子源,可以向各个方向发射某种带负电粒子.已知粒 子的比荷为 ,发射速度大小都为 v0= 。设粒子发射方向与 OC 边的夹角为 θ,不计粒子间相互作用及重 力。对于粒子进入磁场后的运动,下列说法中正确的是 A.当 θ=45°时,粒子将从 AC 边射出 B.所有从 OA 边射出的粒子在磁场中运动时间相等 C.随着 θ 角的增大,粒子在磁场中运动的时间先变大后变小 D.在 AC 边界上只有一半区域有粒子射出 【参考答案】AD 【详细解析】粒子在磁场中做匀速圆周运动,由牛顿第二定律得: ,已知 ,解得 粒子的运动半径 r=L,当 θ=60°入射时,粒子恰好从 A 点飞出,则当 θ=45°时,由几何关系可知,粒子将从 AC 边 射 出 , 选 项 A 正 确 ; 所 有 从 OA 边 射 出 的 粒 子 , θ 不 同 , 而 轨 迹 圆 心 对 应 的 圆 心 角 等 于 ,所用时间 ,T 一定,则知粒子在磁场中时间不 相等,选项 B 错误;当 θ=0°飞 入的粒子在磁场中,粒子恰好从 AC 中点飞出,在磁场中运动时间也恰好是 ;当 θ=60°飞入的粒子在磁场 中运动时间恰好也是 ,是在磁场中运动时间最长,故 θ 从 0°到 60°在磁场中运动时间先减小后增大,当 θ 从 60°到 90°过程中,粒子从 OA 边射出,此时在磁场中运动的时间逐渐减小,故 C 错误;当 θ=0°飞入的粒 子在磁场中,粒子恰好从 AC 中点飞出,因此在 AC.边界上只有一半区域有粒子射出,故 D 正确。 【名师点睛】此题关键要根据磁场的界限来确定运动情况,并结合半径与周期公式来分析讨论.θ 从 0° 到 60°的过程中,粒子在磁场中运动的轨迹对应的圆弧的弦长先减小后增大,所以粒子在磁场中运动时间先 减小后增大是该题的关键。 1.如图所示,有一垂直于纸面向外的有界匀强磁场,磁场的磁感应强度为 B,其边界为一边长为 L 的正三 角形(边界上有磁场),A、B、C 为三角形的三个顶点。现有一质量为 m、电荷量为+q 的粒子(不计重 13 力),以速度 从 AB 边上的某点 P 既垂直于 AB 边又垂直于磁场的方向射入,然后从 BC 边 上某点 Q 射出。若从 P 点射入的该粒子能从 Q 点射出,则) A. B. C. D. 【答案】AD 【解析】带电粒子做匀速圆周运动轨迹的圆心必在 AB 之上,画出运动轨迹如图所示,由半径公式 及 可知,粒子做圆周运动的半径为 ,当粒子运动的轨迹圆心位于 AB 中点 O1 时,粒子正好与 AC、BC 边相切,由几何关系知,PB 满足 ,A 正确;平行向右移动 参考圆 O1,与 CB 交点最远时的 Q 点到 AB 的距离为半径 r,所以 ,D 正确。 2.如图所示,在直角三角形 ABC 内充满垂直纸面向外的匀强磁场(图中未画出),AB 边长度为 d, 。现垂直 AB 边射一群质量均为 m、电荷量均为 q、速度大小均为 v 的带正电粒子,已知垂直 AC 边射出的粒子在磁场中运动的时间为 t0,而运动时间最长的粒子在磁场中的运动时间为 t0(不计重 力)。则下列判断中正确的是 3 4 qBLv m 2 3 4PB L 1 3 4PB L 3 4QB L 1 2QB L mvr qB 3 4 qBLv m 3 4r L 2 3 4PB L 2 3 1 3 2Q r LB π 6B 4 3 14 A.粒子在磁场中做匀速圆周运动的周期为 4t0 B.该匀强磁场的磁感应强度大小为 C.粒子在磁场中运动的轨道半径为 D.粒子进入磁场时速度大小为 【答案】ABC 【解析】带电粒子在磁场中做匀速圆周运动,垂直 AC 边射出的粒子在磁场中运动的时间是 T,即 T=t0,则得周期 T=4t0,故 A 正确。由 得 ,故 B 正确。设运动时间最长的粒 子在磁场中的运动轨迹所对的圆心角为 θ,则有 t0,得 ,画出该粒子的运动轨迹,设轨 道半径为 R,由几何知识得: ,可得 ,故 C 正确。根据 ,解 得 ,故 D 错误,故选:ABC。 (2018·云南省玉溪市高三联合调研)如图所示是某粒子速度选择器截面的示意图,在一半径为R=10 cm 的 圆柱形桶内有 B=10–4 T 的匀强磁场,方向平行于轴线,在圆柱桶某一截面直径的两端开有小孔,作为入射 孔和出射孔。粒子束以不同角度入射,最后有不同速度的粒子束射出。现有一粒子源发射比荷为 的正粒子,粒子束中速度分布连续。当角 θ=45°时,出射粒子速度 v 的大小是 0 π 2 m qt 2 5 d 0 3π 7 d t 1 4 1 4 2πmT qB 0 2π π 2 m mB qT qt =2π T 4 3 2π= 3 cos60cos60 R R d 2 5R d 0 4 3 Rt v 0 π 5 dv t 112 10 C/kgq m 15 A. B. C. D. 【参考答案】B 【详细解析】离子从小孔a 射入磁场,与 ab 方向的夹角为 α=45°,则离子从小孔 b 离开磁场时速度与 ab 的夹角也为 α=45°,过入射速度和出射速度方向作垂线,得到轨迹的圆心 O′,画出轨迹如图,由几何知识得 到 轨 迹 所 对 应 的 圆 心 角 为 : θ=2α=90° , 由 几 何 关 系 知 , 又 , 解 得 : ,故选 B。 1.(2018·云南省曲靖市沾益区四中高二期末)圆形区域内有如图所示的匀强磁场,一束比荷相同的带电粒 子对准圆心 O 射入,分别从 a、b 两点射出,下列说法正确的是 A.b 点出射粒子速率较小 B.a 点出射粒子运动半径较大 C.b 点出射粒子磁场中的运动时间较短 D.a 点出射粒子速度偏转角较小 62 10 m/s 62 2 10 m/s 82 2 10 m/s 64 2 10 m/s 2r R mvr qB 62 2 10 m/sqBrv m 16 【答案】C 【解析】粒子在磁场中做匀速圆周运动,画出粒子运动轨迹的示意图如图所示: 由洛伦兹力提供向心力 ,可得 ,结合几何运动径迹可知,从 b 点射出的粒子运动半径 较大,结合荷质比相同,可得从 a 点射出的粒子速率较小;故 A,B 错误。由运动周期公式得, ,由于荷质比相同,周期与速率无关,粒子运动的时间: 可知运动的时间,仅由轨迹所 对的圆心角 θ 决定,故 b 点射出的粒子运动时间较短;故 C 正确。利用对称性可知,粒子沿半径方向入 射一定沿半径方向出射,由图可以看出 a 粒子速度方向偏转的角度大于 b 粒子速度方向偏转的角度;故 D 错误。 【名师点睛】本题考查带电粒子在有界磁场中的运动,解题关键是要画出粒子轨迹过程图,运用洛伦兹 力提供向心力求出半径公式,注意对称性的运用,粒子沿半径方向入射一定沿半径方向出射,运用粒子 在磁场中转过的圆心角,结合周期公式,求解粒子在磁场中运动的时间. 2.如图所示是一个半径为 R 的竖直圆形磁场区域,磁感应强度大小为 B,磁感应强度方向垂直纸面向内。 有一个粒子源在圆上的 A 点不停地发射出速率相同的带正电的粒子,带电粒子的质量均为 m,运动的半 径为 r,在磁场中的轨迹所对应的圆心角为 α。下列说法正确的是 A.若 r=2R,则粒子在磁场中运动的最长时间为 B.若 r=2R,粒子沿着与半径方向成 45°角斜向下射入磁场,则有关系 成立 π 6 m qB 2 2 1tan 2 7 17 C.若 r=R,粒子沿着磁场的半径方向射入,则粒子在磁场中的运动时间为 D.若 r=R,粒子沿着与半径方向成 60°角斜向下射入磁场,则圆心角 α 为 150° 【答案】BD 【解析】若 r=2R,粒子在磁场中时间最长时,磁场区域的直径是轨迹的一条弦,作出轨迹如图 1 所示, 因为 r=2R,圆心角 θ=60°,粒子在磁场中运动的最长时间 ,故 A 错误。 若 r=2R , 如 图 2 所 示 , 粒 子 沿 着 与 半 径 方 向 成 45° 角 斜 向 下 射 入 磁 场 , 根 据 几 何 关 系 , 有 ,故 B 正确。若 r=R,粒子沿着磁场的半径方向射入,粒子运动轨迹如图 3 所示,圆心角 90°,粒子在磁场中运动的时间 ,故 C 错误。若 r=R,粒子 沿着与半径方向成 60°角斜向下射入磁场,轨迹如图 4 所示,图中轨迹圆心与磁场圆心以及入射点和出 射点构成菱形,圆心角 150°,故 D 正确。 图 1 图 2 图 3 图 4 如图所示,正六边形 abcdef 区域内有垂直于纸面的匀强磁场。一带正电的粒子从 f 点沿 fd 方向射入磁 场区域,当速度大小为 vb 时,从 b 点离开磁场,在磁场中运动的时间为 tb,当速度大小为 vc 时,从 c 点离 开磁场,在磁场中运动的时间为 tc,不计粒子重力。则 π 3 m qB max 60 2π 1 π=360 6 3 m mt T qB qB 2 2 2 12tan 2 72 2 R r R 90 2π 1 π=360 4 2 m mt T qB qB 18 A.vb:vc=2:2,tb:tc=1:2 B.vb:vc=1:2,tb:tc=2:1 C.vb:vc=2:1,tb:tc=2:1 D.vb:vc=1:2,tb:tc=1:2 【参考答案】B 【详细解析】粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,根据牛顿第二定律有 得 ;粒子在磁场中运动的轨迹如图,从 b 点离开磁场的粒子,圆心在 a 点,半径等于正六边形的边 长,即 rb=a;从 c 点离开磁场的粒子,圆心是 O 点,半径等于正六边形边长的 2 倍,即 rc=2a;根据半径公 式 得 , ,从 b 点离开磁场的粒子,圆心角 θb=120°;从 c 点离开磁场的粒 子,圆心角 θc=60°;根据 ,得 ,故 B 正确,ACD 错误。 1.如图所示,截面为正方形的容器在匀强磁场中,一束电子从 a 孔垂直于磁场射入容器中,其中一部分从 c 孔射出,一部分从 d 孔射出,忽略电子间的作用,下列说法正确的是 A.从 cd 两孔射出的电子速度之比为 v1:v2=2:1 B.从 cd 两孔射出的电子在容器中运动所用的时间之比为 t1:t2=1:2 C.从 cd 两孔射出的电子在容器中运动时的加速度大小之比为 a1:a2=2:1 D.从 cd 两孔射出电子在容器中运动时的加速度大小之比为 a1:a2= :1 2vqvB m r mvr qB mvr qB qBrv rm 1 2 b b c c v r v r 360t T 2 1 b b c c t t 2 19 【答案】ABC 【解析】设磁场边长为 a,如图所示,粒子从 c 点离开,其半径为 rc,粒子从 d 点离开,其半径为 rd; 由 ,得出半径公式 ,又由运动轨迹知 rc=2rd 则 vc:vd=2:1,故 A 正确。由 , 根据圆心角求出运行时间 ;运行时间 , ,则 tc:td=1:2,故 B 正确。向心加速度: ,则 ac:ad=2:1,故 C 正确,D 错误。 2.(2018·湖北省荆州市高二期末)如图所示,在一个边长为 的正六边形区域内存在磁感应强度为 ,方 向垂直于纸面向里的匀强磁场。三个相同的带电粒子,比荷大小均为 ,先后从 点沿 方向以大 小不等的速度射人匀强磁场区域,粒子在运动过程中只受磁场力作用。已知编号为 的粒子恰好从 点飞出磁场区域,编号为 的粒子恰好从 点飞出磁场区城,编号为 的粒子从 边上的某点垂直 边界飞出磁场区城。则 A.三个带电粒子均带正电 B.编号为 的粒子进人磁场区城的初速度大小为 C.编号为 的粒子在磁场区城内运动的时间为 D.编号为 的粒子在 边上飞出的位置与 点的距离为 【答案】ABD 【解析】由于三个粒子的偏转方向均向上,根据左手定则可知,三个粒子带同种正电荷,故A 正确;根 据题意作出三个粒子的运动轨迹,如图所示: 2vqvB m r mvr qB 2πmT qB 2πt T 2d Tt 4d Tt 2va r a B q m A AD 1q F 2q E 3q ED 1q 3 3 Bqa m 2q π 6 m Bq 3q ED E 2 3 3 a 20 设编号为 的粒子在正六边形区域磁场中做圆周运动的半径为 ,初速度大小为 ,由几何关系得: ,根据 ,解得: ,故 B 正确;设编号为 的粒子在正六边 形区域磁场中做圆周运动的半径为 ,初速度大小为 ,周期为 ,由几何关系可得,粒子在 正六边形区域磁场运动过程中,转过的圆心角为 ,则粒子在磁场中运动的时间 ,故 C 错误;设编号为 的粒子在正六边形区域磁场中做圆周运动的半径为 ,在磁场中转了 ,由几何关 系 可 得 : , , , 则 ,故 D 正确;故选 ABD。 【名师点睛】分析各粒子的运动情况,由几何关系求出各自的半径,再由洛伦兹力充当向心力即可求得 速度大小;再根据几何关系求出圆心角,再根据时间与周期间的关系即可明确时间大小。 1.带电粒子以一定速度垂直射入匀强磁场,若只考虑洛伦兹力,则粒子的 A.速度不变 B.动能不变 C.加速度不变 D.受力不变 2.(2018·百校联盟高考名师猜题保温金卷)如图所示,半径为 R 的半圆形有界磁场关于 x 轴对称,y 轴刚 好与磁场左边界在坐标原点处相切,在坐标原点处有一粒子源,可以沿 x 轴正方向连续地发射质量为 m, 1q 1r 1v 1 3 2 60 3 a ar sin 2 1 1 1 vqv B r 1 3 3 qBav m 2q 2r 2v 2 2πmT qB 60 2 2 6 3 T mt qB 3q 3r 30 2 cos30 3AE a a 3 2 3sin30 AEr a 3 3tan30 AEO E a 3 3 2 3 3EG r O E a 21 电荷量大小为 q 的不同速率的正、负电荷。已知磁场的方向垂直于坐标平面向里,磁感应强度大小为 B, 若粒子不能从半圆的直径部分射出,则 A.粒子在磁场中运动的最大半径可能为 R B.粒子在磁场中运动的最大速度可能为 C.粒子在磁场中运动扫过的面积最大可能为 D.粒子在磁场中运动的最短时间可能为 3.关于磁场,下列说法中正确的是 A.指南针的使用,说明地球有磁场 B.磁场的方向与放在该点的通电直导线所受磁场力方向一致 C.带电物体在磁场中所受的洛伦兹力不可能为零 D.磁感应强度越大,线圈面积越大,则穿过线圈的磁通量也越大 4.(2018·陕西省高三教学质量检测)磁流体发电是一项新兴技术。如图所示,平行金属板之间有一个很强的 磁场,将一束含有大量正、负带电粒子的的等离子体,沿图中所示方向喷入磁场,图中虚线框部分相当于 发电机,把两个极板与用电器相连,则 A.用电器中的电流方向从 B 到 A B.用电器中的电流方向从 A 到 B C.若只增大带电粒子电荷量,发电机的电动势增大 D.若只增大喷入粒子的速度,发电机的电动势增大 5.如图所示,甲带正电,乙是不带电的绝缘物块,甲、乙叠放在一起,置于粗糙的固定斜面上,地面上方 空间有垂直纸面向里的匀强磁场,现用平行于斜面的力 F 拉乙物块,使甲、乙一起无相对滑动沿斜面向 2 qBR m 2π 1 R( ) π 2 m qB 22 上作匀加速运动的阶段中 A.甲、乙两物块间的摩擦力不断增大 B.甲、乙两物块间的摩擦力保持不变 C.甲、乙两物块间的摩擦力不断减小 D.乙物块与斜面之间的摩擦力不断增大 6.(2018·贵州省遵义高三模拟)如图所示,套在足够长的绝缘粗糙直棒上的带正的电小球,其质量为 m, 带电荷量为 q,小球可在棒上滑动。现将此棒竖直放入沿水平方向且互相垂直的匀强磁场和匀强电场中, 设小球所带电荷量不变,在小球由静止下滑的过程中 A.小球的加速度一直增大 B.小球的速度一直增大,直到最后匀速 C.小球的速度先增大,再减小,直到停止运动 D.棒对小球的弹力一直减小 7.(2018·江西省浮梁一中高考冲刺训练卷)据有关资料介绍,受控核聚变装置中有极高的温度,因而带电 粒子将没有通常意义上的“容器”可装,而是由磁场约束带电粒子运动,使之束缚在某个区域内。如图所 示,环状磁场的内半径为 R1,外半径为 R2,被束缚的带电粒子的比荷为 k,中空区域内带电粒子具有各 个方向的速度,速度大小为 v。中空区域中的带电粒子都不会穿出磁场的外边缘而被约束在半径为 R2 的 区域内,则环状区域内磁场的磁感应强度大小可能是 A. 2 2 1 2R v k R R( ) 23 B. C. D. 8.如图所示,在圆形区域内存在垂直纸面向外的匀强磁场,ab 是圆的直径,一不计重力的带电粒子从 a 点 射入磁场,速度大小为 ,当速度方向与 ab 成 30°角时,粒子在磁场中运动的时间最长,且为 t;若相 同的带电粒子从 a 点沿 ab 方向射入磁场,也经时间 t 飞出磁场,则其速度大小为 A. B. C. D. 9.一质量为 m、带电量为 q 的粒子以速度 从 O 点沿 y 轴正方向射入磁感强度为 B 的一圆形匀强磁场区域, 磁场方向垂直于纸面,粒子飞出磁场区后,从 b 处穿过 x 轴,速度方向与 x 轴正向夹角为 30°,如图所 示(粒子重力忽略不计)。试求: (1)圆形磁场区的最小面积; (2)粒子从 O 点进入磁场区到达 b 点所经历的时间; (3)b 点的坐标。 10.(2018·安徽省六安二中河西校区高二期末)如图所示,以 O 为圆心、半径为 R 的圆形区域内存在垂直 圆面向里、磁感应强度为 B 的匀强磁场,一粒子源位于圆周上的 M 点,可向磁场区域内垂直磁场沿各 个方向发射质量为 m、电荷量为 的粒子,不计粒子重力,N 为圆周上另一点,半径 OM 和 ON 间的 2 2 2 2 1 2R v k R R( ) 2 1 3v k R R( ) 2 1 v k R R( ) v 3 2 v 1 2 v 3 6 v 2 3 v 0v q 24 夹角 ,且满足 . (1)若某一粒子以速率 v ,沿 MO 方向射入磁场,恰能从 N 点离开磁场,求此粒子的速率移 v ; (2)若大量此类粒子以速率 ,从 M 点射入磁场,方向任意,则这些粒子在磁场中运动的 最长时间为多少? (3)若由 M 点射入磁场各个方向的所有粒子速率均为题 中计算出的 ,求磁场中有粒子通过 的区域面积。 11.(2018·广东省七校联合体高三第三次联考)如图所示,PQMN 是竖直面内一边长为 L 的正方形区域, 区域内有竖直向上的匀强电场,场强为 E,在△PQM 中还存在水平向里的匀强磁场,磁感强度为 B; 在 PQMN 的左侧有一足够长的粗糙绝缘细杆,细杆与 PQ 在同一水平线上,细杆周围存在水平方向足 够长匀强磁场,磁感强度 B0(大小可调的),方向水平向里。细杆的左侧套有一带电荷量为+q 的小球, 现使小球以适当的速度沿杆向右运动,在到达 P 点前小球已匀速运动,由 P 点射入△PQM 区域后,小 球做匀速圆周运动,已知重力加速度为 g: (1)小球在细杆上做什么运动?请直接用文字描述 (2)若小球恰能从 M 点离开电磁场,求小球的质量和粒子从 P 点射入到从 M 点离开电磁场这段时间 内的平均速度的大小和方向; (3)若调节 B0 的大小,从而改变小球由 P 点射入电磁场的速度,使小球最终从 Q 点离开磁场,求此 过程中重力势能变化的最大值; (4)若调节 B0 的大小,使小球由 P 点射入电磁场后最终由 NP 射出,求 B0 的最小值。 tan 0.52 1 1 2 2qBRv m 1 1v 25 12.(2018·北京卷)某空间存在匀强磁场和匀强电场。一个带电粒子(不计重力)以一定初速度射入该空间 后,做匀速直线运动;若仅撤除电场,则该粒子做匀速圆周运动,下列因素与完成上述两类运动无关 的是 A.磁场和电场的方向 B.磁场和电场的强弱 C.粒子的电性和电量 D.粒子入射时的速度 13.(2017·新课标全国Ⅱ卷)如图,虚线所示的圆形区域内存在一垂直于纸面的匀强磁场,P 为磁场边界 上的一点。大量相同的带电粒子以相同的速率经过 P 点,在纸面内沿不同的方向射入磁场。若粒子射 入速率为 ,这些粒子在磁场边界的出射点分布在六分之一圆周上;若粒子射入速率为 ,相应的出 射点分布在三分之一圆周上。不计重力及带电粒子之间的相互作用。则 为 A. B. C. D. 14.(2016·新课标全国Ⅱ卷)一圆筒处于磁感应强度大小为 B 的匀强磁场中,磁场方向与筒的轴平行,筒 的横截面如图所示。图中直径 MN 的两端分别开有小孔,筒绕其中心轴以角速度 ω 顺时针转动。在该 截面内,一带电粒子从小孔 M 射入筒内,射入时的运动方向与 MN 成 30°角。当筒转过 90°时,该粒子 恰好从小孔 N 飞出圆筒。不计重力。若粒子在筒内未与筒壁发生碰撞,则带电粒子的比荷为 A. B. C. D. 1v 2v 2 1:v v 3 : 2 2 :1 3 :1 3: 2 3B 2B B 2 B 26 15.(2016·新课标全国Ⅲ卷)平面OM 和平面 ON 之间的夹角为 30°,其横截面(纸面)如图所示,平面 OM 上方存在匀强磁场,磁感应强度大小为 B、方向垂直于纸面向外。一带电粒子的质量为 m,电荷量为 q (q>0)。粒子沿纸面以大小为 v 的速度从 OM 的某点向左上方射入磁场,速度与 OM 成 30°角。已知 该粒子在磁场中的运动轨迹与 ON 只有一个交点,并从 OM 上另一点射出磁场。不计重力。粒子离开 磁场的出射点到两平面交线 O 的距离为 A. B. C. D. 2.AD【解析】粒子不能从半圆的直径部分射出,则半径最大的是轨迹刚好与直径相切,由几何关系可知 这时的粒子运动半径为 R,选项 A 正确;最大半径对应着最大速度,由 得 ,选项 B 错误; 粒子在磁场中运动扫过的面积最大可能为 ,选项 C 错误;粒子在磁场中运动 的轨道半径越大,运动轨迹所对的圆心角越小,因此最小时间为 ,选项 D 正确。 3.A【解析】指南针是由磁性材料做成的,指南针指南说明它受到磁场的作用,说明地球周围有磁场,A 正确;根据左手定则,可得磁场的方向与放在该点的通电直导线所受磁场力方向垂直,B 错误;当带电 物体的运动方向和磁场方向平行时,不受洛伦兹力作用,C 错误;在计算磁通量的公式 中 S 指的 是磁场穿过线圈的有效面积,不一定等于线圈面积,D 错误。 4.BD【解析】首先对等离子体进行动态分析:开始时由左手定则判断正离子所受洛伦兹力方向向上(负离 2 mv qB 3mv qB 2mv qB 4mv qB mvR qB qBRv m 2 2 21 14 π π 24 2R R R ( )( ) 1 π 4 2 mT qB BS 27 子所受洛伦兹力方向向下),则正离子向上板聚集,负离子则向下板聚集,两板间产生了电势差,即金 属板变为一电源,且上板为正极下板为负极,所以通过用电器的电流方向从 A 到 B,选项 A 错误,选项 B 正确;此后的正离子除受到向上的洛伦兹力 f 外还受到向下的电场力 F,最终两力达到平衡,即最终 等离子体将匀速通过磁场区域,因 f=qvB, ,则: ,解得 E=Bdv,所以电动势 E 与速 度 v 及磁场 B 成正比,与带电粒子的电荷量无关,选项 C 错误,选项 D 正确。~网 【名师点睛】正确分析离子的受力情况是解决本题的关键。先根据左手定则判断等离子体的正离子(或 负离子)所受洛伦兹力的方向,从而知道金属板的电势高低,进一步受力分析结合牛顿第二定律可得出 最终等离子体做匀速直线运动,根据洛伦兹力等于电场力,分析电动势的决定因素。 5.B【解析】对整体,分析受力情况:重力、斜面的支持力和摩擦力、拉力 F 和洛伦兹力,洛伦兹力方向 垂直于斜面向上,则由牛顿第二定律得:F–m 总 gsin α–μFN=m 总 a①;FN=m 总 gcos α–F 洛②,随着速度的 增大,洛伦兹力增大,则由②知:FN 减小,乙所受的滑动摩擦力 f=μFN 减小;以甲为研究对象,有:m 甲 gsin θ–f=m 甲 a③;由①知,f 减小,加速度不变,因此根据③可知,甲乙两物块之间的摩擦力保持不变, 故 B 正确,ACD 错误;故选 B。 7.B【解析】粒子沿环状的半径方向射入磁场,不能穿越磁场区域的最大速度粒子沿圆弧从 B 到 A,恰与 环状域外圆相切,如图所示: 为轨迹圆心。设 AO′=BO′=r,由几何关系得 ,由牛 顿第二定律可知: ,解得: ,联立解得: ,故 B 正确,ACD 错误。 EF q d EqvB q d O 2 2 2 2 1R r r R 2vqvB m r mvr qB 2 2 2 2 1 2R vB k R R 28 [来源:Z|xx|k.Com] 9.(1) (2) (3) 2 2 0 2 2 3π 4 m v q B 2π( 3)3 m qB 03 0( )mv Bq , 29 (2)粒子从 O 至 a 做匀速圆周运动的时间 从 a 飞出磁场后做匀速直线运动,所以 , 所以 (3)因为 , ,所以 ,故 b 点坐标为 【名师点睛】带电粒子在匀强磁场中运动时,洛伦兹力充当向心力,从而得出半径公式 ,周期 公式 ,运动时间公式 ,知道粒子在磁场中运动半径和速度有关,运动周期和速度无 关,画轨迹,定圆心,找半径,结合几何知识分析解题。¥网 10.(1) (2) (3) [来源:Zxxk.Com] 【解析】(1)粒子以速率 沿 MO 方向射入磁场,恰能从 N 点离开磁场,轨迹如图: 设轨迹半径为 ,则 1 2π 3 3 T mt qB tan30 3R ab R ab 2 0 0 3 3ab R mt v v qB 1 2 2π( 3)3 mt t t qB sin30 R O b 2O b R 033 mvOb R Bq 03 0( )mv Bq , mvR Bq 2πmT Bq 2πt T 1 2 qBRv m 3 mt Bq 2 211 3 24 4 RS R 1v 1r 1 2 rtan R 30 解得: 由牛顿第二定律可得 解得: 粒子方向任意,粒子在磁场中运动时间最长时,弧长(劣弧)最长,对应的弦长最长(磁场圆的直 径),轨迹如图: 则 解得: 粒子在磁场中运动的最长时间 1 2 Rr 2 1 1 1 vqv B m r 1 2 qBRv m 2 Rsin r 6 2 2 2 3max r mt v qB 31 、 、 所以 【名师点睛】本题的难点在第三问,要找到粒子能到达的区域,首先要考虑的是粒子的偏转方向--顺时 针;其次要考虑的极端情况①从 M 点竖直向上射出,则可以做完整的圆周运动。②然后把这个完整的 圆绕 M 点转动 1800,则该圆与磁场区域公共部分,就是粒子能达到的区域。 11.(1)小球在细杆上做加速越来越小的减速运动最后匀速运动[来源:Z.xx.k.Com] (2) 平均速度方向由 P 点指向 M 点 (3) (4) 【解析】(1)小球在细杆上做加速度越来越小的减速运动,最后匀速运动。 (2)小球在电磁场中匀速圆周运动有:mg=qE 可得 由几何关系可知 r1=L,且 小球从 P 点到 M 点的位移 s= L t= T 则小球的平均速度 平均速度的方向由 P 点指向 M 点 2 2 1 1 2 2 8 R RS 2 2 1 6S R 2 2 2 2 3 1 1 3 1 3 6 2 2 6 4S R R R R 2 211 3 24 4S R R 2 2 π gBL E 2 2 8 qgB LqEL E min 3EB gBL qEm g 2 1 1 1 vqv B m r 1 1 2π 2π 2πr m ET v qB gB 2 1 2 2 2 π s gBLv t E 32 小球以 v2 竖直向上过 MP,在△PMN 中匀速直线运动,再以 v2 竖直过 MN,当小球的加速度为零时, 重力势能变化量最大为 (4)当 B0 取最小值时 v 最大,在电磁场中运动半径最大,小球能由 PQ 射出,有几何关系可知,半径 由 得 在细杆上有 可得: 12.C【解析】由题可知,当带电粒子在复合场内做匀速直线运动,即 .,则 .,若 仅撤除电场,粒子仅在洛伦兹力作用下做匀速圆周运动,说明要满足题意需要对磁场与电场的方向以 及强弱程度都要有要求,例如:电场方向向下,磁场方向垂直纸面向里等,但是对电性和电量无要求, 故选项 C 正确,ABD 错误。 【名师点睛】本题考查了带电粒子在复合场中的运动,实际上是考查了速度选择器的相关知识,注意 当粒子的速度与磁场不平行时,才会受到洛伦兹力的作用,所以对电场和磁场的方向有要求的。 2 2 2 pm 2 1Δ 2 8 qgB LE mgL mv qEL E 2 1 3r L 2 3 3 3 vqv B m r 3 3 gBLv E 3 0minqv B mg min 3EB gBL Eq qvB Eq qvB Ev B 33 【名师点睛】此题是带电粒子在有界磁场中的运动问题;解题时关键是要画出粒子运动的轨迹草图, 知道能打到最远处的粒子运动的弧长是半圆周,结合几何关系即可求解。 14.A【解析】作出粒子的运动轨迹,由几何知识可得,轨迹的圆心角为 ,两个运动具有等 时性,则 ,解得 ,故选 A。 【名师点睛】此题考查带电粒子在匀强磁场中的运动问题;解题时必须要画出规范的粒子运动的草图, 结合几何关系找到粒子在磁场中运动的偏转角,根据两个运动的等时性求解未知量;此题难度中等, 意在考查考生对物理知识与数学知识的综合能力。%网 15.D【解析】根据题意,粒子在磁场中的运动轨迹与ON 只有一个交点,则轨迹与 ON 相切,设切点为 C 点,入射点为 D 点,出射点为 A 点,粒子在磁场中的轨迹圆心为 点,根据几何知识可得 ,则三角形 AB 为等边三角形,故∠ AB=60°,而∠MON=30°,∠OCA=90°, 故 C A 为 一 条 直 线 , 所 以 △AOC 为 直 角 三 角 形 , 故 粒 子 离 开 磁 场 的 出 射 点 到 O 的 距 离 为 ,而半径公式 ,故距离为 ,D 正确。 【名师点睛】带电粒子在匀强磁场中运动时,洛伦兹力充当向心力,从而得出半径公式 ,周期 公式 ,运动时间公式 ,知道粒子在磁场中运动半径和速度有关,运动周期和速度无 关,画轨迹,定圆心,找半径,结合几何知识分析解题。 π π π( ) 24 3 6 π 60 2π 2 360 m qB 3 q m B O 2 sin30AD r r O O O 2= =4sin30 sin30 AC rAO r mvr Bq 4mv Bq mvR Bq 2πmT Bq 2πt T查看更多