湖南省四校2019届高三摸底调研联考试题 理科数学(解析版)

湖南省四校2019届高三摸底调研联考试题 理科数学(解析版)

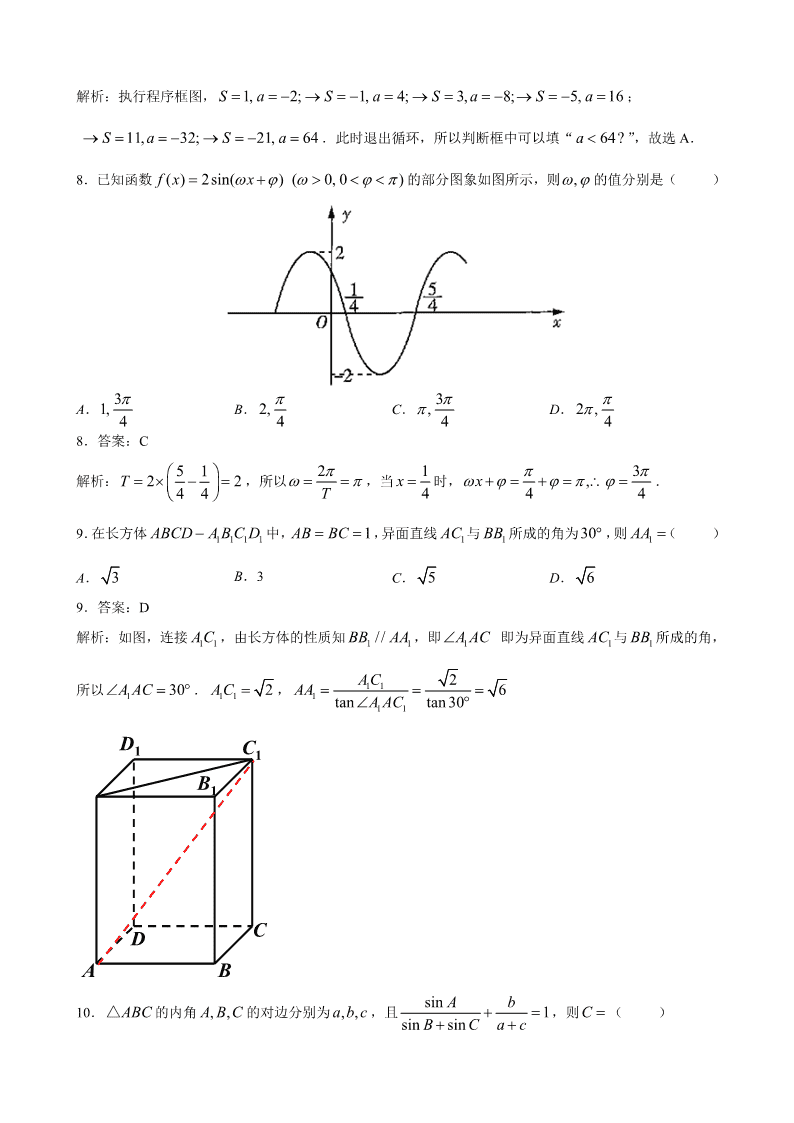
湖南省四校 2019 届高三摸底调研联考试题 理科数学 一、选择题：本题共 12 小题，每小题 5 分，共 60 分．在每小题给出的四个选项中，只有一项是符合题目 要求的． 1．设复数 1 i 2i1 iz   ，则 z  （ ） A．0 B．1 C．2 D．3 1．答案：D 解析： 3 3i1 i 3 3i 3 22i 31 i 1 i 1 i 2 z          ． 2．已知集合 2{ | 1 1}, { | 2 0}A x x B x x x        ，则 R A B  （ ） A．( 1,0] B．[ 1,2) C．[1,2) D．(1,2] 2．答案：C 解析： { | 1A x xR ≥ 或 1}x ≤ ，又 2{ | 2 0} { | 1 2}B x x x x x        ， 所以  { |1 2}A B x x R  ≤ ． 3．甲、乙两名同学 6 次考试的成绩如图所示，且这 6 次成绩的平均分分别为 ,x x甲 乙 ，标准差分别为 , 甲 乙 ， 则（ ） A． ,x x   甲 乙 甲 乙 B． ,x x   甲 乙 甲 乙 C． ,x x   甲 乙 甲 乙 D． ,x x   甲 乙 甲 乙 3．答案：C 解析：由题图可知，甲同学除第 2 次考试成绩低于乙同学外，其他 5 次考试成绩都高于乙同学，所以 x x甲 乙 ．又由题图中数据知甲同学的成绩波动没有乙同学的成绩波动大，所以甲同学的成绩更稳定，所 以  甲 乙 ． 4． 计算sin133 cos197 cos 47 cos73    的结果为（ ） A． 1 2 B． 1 2 C． 2 2 D． 3 2 4．答案：B 解析：sin133 cos197 cos 47 cos 73 sin 47 cos17 cos 47 sin17 sin(17 47 )                1sin( 30 ) sin 30 2        ． 5．已知 , ,A B P 是双曲线 2 2 2 2 1( 0, 0)x y a ba b    上不同的三点，且 ,A B 连线经过坐标原点，若直线 ,PA PB 的斜率乘积 3PA PBk k  ，则该双曲线的离心率为（ ） A． 2 B． 3 C．2 D．3 5．答案：C 解析：由双曲线的对称性知，点 ,A B 关于原点对称，设 1 1 1 1 2 2( , ), ( , ), ( , )A x y B x y P x y  ，则 2 2 2 2 1 1 2 2 2 2 2 21, 1x y x y a b a b    ，两式相减，得 2 2 2 2 1 2 1 2 2 2 x x y y a b   ，又 1 2 1 2 1 2 1 2 ,PA PB y y y yk kx x x x     ，所以 2 2 2 1 2 2 2 2 1 2 3PA PB y y bk k x x a     ，所以离心率 2 21 2be a   ． 6． 9 2 12x x     的展开式中的常数项为（ ） A．672 B． 672 C．84 D． 84 6．答案：A 解析：展开式中的常数项为 6 6 2 3 9 1(2 ) 672C x x      ． 7．运行如图所示的程序框图，若输出的 S 的值为 21 ，则判断框可以填（ ） A． 64?a  B． 64?a ≤ C． 128?a  D． 128?a ≤ 7．答案：A 解析：执行程序框图， 1, 2; 1, 4; 3, 8; 5, 16S a S a S a S a               ； 11, 32; 21, 64S a S a        ．此时退出循环，所以判断框中可以填“ 64?a  ”，故选 A． 8．已知函数 ( ) 2sin( ) ( 0, 0 )f x x         的部分图象如图所示，则 ,  的值分别是（ ） A． 31, 4  B． 2, 4  C． 3, 4  D． 2 , 4  8．答案：C 解析： 5 12 24 4T        ，所以 2 T    ，当 1 4x  时， 3,4 4x            ． 9．在长方体 1 1 1 1ABCD A B C D 中， 1AB BC  ，异面直线 1AC 与 1BB 所成的角为30 ，则 1AA （ ） A． 3 B．3 C． 5 D． 6 9．答案：D 解析：如图，连接 1 1AC ，由长方体的性质知 1 1//BB AA ，即 1A AC 即为异面直线 1AC 与 1BB 所成的角， 所以 1 30A AC  ． 1 1 2AC  ， 1 1 1 1 1 2 6tan tan 30 ACAA A AC    A B CD D1 C1 B1 10． ABC△ 的内角 , ,A B C 的对边分别为 , ,a b c ，且 sin 1sin sin A b B C a c   ，则C  （ ） A． 6  B． 3  C． 2 3  D． 5 6  10．答案：B 解析：由 sin 1sin sin A b B C a c   及正弦定理可得 1a b b c a c   ，整理可得 2 2 2a b c ab   ．由余弦 定理知 2 2 2 1cos 2 2 a b cC ab    ，又 (0, )C  ，所以 3C  ． 11．已知 F 是抛物线 2: 8C y x 的焦点，M 是C 上一点，FM 的延长线交 y 轴于点 N ．若 M 为 FN 的 中点，则 FN  （ ） A．4 B．6 C．8 D．10 11．答案：B 解析：如图，不妨设点 M 位于第一象限，设抛物线的准线 : 2l x   与 x 轴交于点 K ，做 MB l 于点 B ， NA l 于点 A ，则 2, 4AN FK  ，在直角梯形 ANFK 中，由中位线定理，知 32 AN FKBM   ， 由抛物线的定义知 3MF MB  ，所以 3MN MF  ， 6FN FM MN   ． B A K M N FO 12．已知函数 2( )f x a x  （ 1 ,x e ee ≤ ≤ 为自然对数的底数）与 ( ) 2lng x x 的图象上存在关于 x 轴 对称的点，则实数 a 的取值范围是（ ） A． 2 11, 2e     B． 2[1, 2]e  C． 2 2 1 2, 2ee      D． 2[ 2, )e   12．答案：B 解析：由条件知，方程 2 2lna x x   ，即 2 2lna x x  在 1 ,ee      上有解．设 2( ) 2lnh x x x  ，则 2 2( 1)( 1)( ) 2 x xh x x x x      ．当 1 ,1x e     时， ( ) 0, ( )h x h x  单调递减；当 (1, )x e 时， ( ) 0, ( )h x h x  单调递增，所以 min( ) (1) 1h x h  ．又 2 2 1 1 2, ( ) 2h h e ee e         ，所以 1( )h e h e      ， 所以 2 2lna x x  在 1 ,ee      上有解等价于 21 2a e ≤ ≤ ，所以实数 a 的取值范围是 2[1, 2]e  ． 二、填空题：本题共 4 小题，每小题 5 分，共 20 分．把答案填在题中的横线上． 13．已知向量 (1,1) ( 3, 2)a b    ，若向量 2ka b  与 a 垂直，则实数 k  ． 13．答案： 1 解析： 2 ( 6, 4)ka b k k     ，又因为 2ka b a    ，  2 6 4 0ka b a k k          ，解得 1k   ． 14．已知实数 ,x y 满足约束条件 2 0 6 0 2 3 0 x y x y x y        ≥ ≤ ≤ ，则 2 3z x y  的最小值是 ． 14．答案： 8 解析：作可行域为如图所示的 ABC△ ，其中 ( 1, 2), (5,1), (2, 4)A B C  ，则 4, 7, 8A B Cz z z    ， min 8Cz z    ． x y O A B C 15．已知定义在 R 上的奇函数 ( )f x 满足 5 ( ) 02f x f x      ，当 5 04 x ≤ ≤ 时， ( ) 2xf x a  ，则 (16)f  ． 15．答案： 1 2 解析：由 5 ( ) 02f x f x      ，得 5( 5) ( )2f x f x f x        ，所以函数 ( )f x 是以 5 为周期的周期 函数，则 (16) (1)f f ，又 ( )f x 是奇函数，所以 (0) 1 0, 1f a a      ，所以当 5 04 x ≤ ≤ 时， ( ) 2 1xf x   ，所以 1( 1) 2f    ，则 1(1) ( 1) 2f f    ，故 1(16) 2f  ． 16．在四棱锥 S ABCD 中，底面 ABCD 是边长为 2 的正方形，侧面 SAD 是以 SD 为斜边的等腰直角三 角形，若四棱锥 S ABCD 体积的取值范围为 4 3 8,3 3       ，则该四棱锥外接球表面积的取值范围是 ． 16．答案： 28 ,203       解析：在四棱锥 S ABCD 中，由条件知 , ,AD SA AD SB SA AB A   ，所以 AD  平面 SAB ，所 以是圆柱模型，所以平面 SAB  平面 ABCD ．设 SAB   ，则 1 8 4 3 8sin ,3 3 3 3S ABCD ABCDV S SO          ，所以 3sin ,12      ， 2,3 3       ， 所以 1 1cos2 2 ≤ ≤ ，在 SAB△ 中， 2SA AB  ，所以 2 2 1 cosSB    ，所以 SAB△ 的外接 圆半径为 2 1 cos 2sin sin SBr      ．外接球半径 2 1R r  ，所以该四棱锥外接球的表面积 2 2 2 284 4 ( 1) 4 1 , 201 cos 3S R r                    ． S A O B C D 三、解答题：共 70 分．解答应写出文字说明、证明过程或演算步骤．第 17~21 题为必考题，每个试题考 生都必须作答．第 22、23 题为选考题，考生根据要求作答． （一）必考题：共 60 分． 17．（本小题满分 12 分） 已知数列{ }na 的前 n 项和为 nS ，且 2 2n nS a  ． （1）求数列{ }na 的通项公式； （2）若 n nb na ，求数列{ }nb 的前 n 项和 nT ． 17．解析：（1） 2 2n nS a  ① ， 1 12 2 ( 2)n nS a n    ②≥ ， ① ② 得， 1 12 2n n n n nS S a a a     ， 12 ( 2, )n na a n n    N≥ ， 在①式中，令 1n  ，得 1 2a  ， 所以数列{ }na 是首项为 2，公比为 2 的等比数列， 2n na  ．………………………………5 分 （2）由（1）得， 2n nb n  ， 2 3 1 2 3 4 1 1 2 2 2 3 2 ( 1) 2 2 2 1 2 2 2 3 2 ( 1) 2 2 n n n n n n T n n T n n                              ③ ④ ③ ④ 得， 2 3 1 1 1 1 12 2 2 2 2 2 2 2 2 (1 ) 2 2n n n n n n nT n n n                     ， 1( 1) 2 2n nT n      ．……………………………………………………………………………………12 分 18．（本小题满分 12 分） 某家电公司销售部门共有 200 名销售员，每年部门对每名销售员都有 1 400 万元的年度销售任务．已知这 200 名销售员的销售额都在区间[2, 22]（单位：百万元）内，现将其分成 5 组，第 1 组、第 2 组、第 3 组、 第 4 组、第 5 组对应的区间分别为[2, 6)，[6, 10)，[10,14)，[14,18)，[18, 22]，并绘制如下的频率分布直方 图． （1）求 a 的值，并计算完成年度任务的人数； （2）用分层抽样的方法从这 200 名销售员中抽取容量为 25 的样本，求这 5 组分别应抽取的人数； （3）现从（2）中完成年度任务的销售员中随机选取 2 名，奖励海南三亚三日游，求获得此奖励的 2 名销 售员在同一组的概率． 18．解析：（1） (0.02 0.08 0.09 2 ) 4 1, 0.03a a       ， ∴完成年度任务的人数为 2 0.03 4 200 48    ．…………………………………………………4 分 （2）第 1 组应抽取的人数为 0.02 4 25 2   ，第 2 组应抽取的人数为 0.08 4 25 8   ， 第 3 组应抽取的人数为0.09 4 25 9   ，第 4 组应抽取的人数为0.03 4 25 3   ， 第 5 组应抽取的人数为0.03 4 25 3   ．……………………………………………………………8 分 （3） 在（2）中完成年度任务的销售员中，第 4 组有 3 人，第 5 组有 3 人， 从这 6 人中随机选取 2 名，共有 2 6 15C  个基本事件，其中 2 名销售员来自同一组的事件数为 2 2 3 3 6C C  ， 所以所求概率 6 2 15 5P   ．…………………………………………………………………………12 分 19．（本小题满分 12 分） 如图，正三棱柱 1 1 1ABC A B C 的所有棱长都为 2， D 为 1CC 的中点． （1）求证： 1AB  平面 1A BD ； （2）求锐二面角 1A A D B  的余弦值． A B C D A1 B1 C1 19．解析：（1）取 BC 的中点O ，连接 1,AO B O ， ABC△ 为正三角形， AO BC  ， 在正三棱柱 1 1 1ABC A B C 中，平面 ABC  平面 1 1BCC B ，平面 ABC  平面 1 1BCC B BC ． AO  平面 ABC ，且 AO BC ， AO  平面 1 1BCC B ，而 BD  平面 1 1BCC B ， AO BD  ， 在正方形 1 1BCC B 中，易证得 1 1,BCD B BO CBD BB O  △ ≌△ ， 1 1 1 90CBD BOB BB O BOB         ， 1BD OB  ，又 1AO OB O ， BD  平面 1AOB ， 1BD AB  ，在正方形 1 1ABB A 中，有 1 1A B AB ，又 1BD A B B ， 1AB  平面 1A BD ．……………………………………………………………………………………6 分 （2）取 1BC 的中点 1O ，连接 1OO ，以O 为原点， 1, ,OB OO OA    的方向分别为 , ,x y z 轴的正方向建立空 间直角坐标系O xyz ，如图所示，则 1 1(0,0, 3), ( 1,0,0), ( 1,2,0), (1,2,0)A C C B  ， 1(1,0, 3), (0,2,0)AC CC    ，设平面 1A AD 的法向量 ( , , )n x y z ， 则 1 3 0 2 0 n AC x z n CC y             ，令 1z   ，得 3x  ， ( 3,0, 1)n   ， 由（1）知 1AB  平面 1A BD ， 1 (1,2, 3)AB    为平面 1A BD 的一个法向量， 1 1 1 2 3 6cos , 42 2 2 n ABn AB n AB           ，∴锐二面角 1A A D B  的余弦值为 6 4 ．…………12 分 A B C O C1 A1 B1 D O1 x y z 20．（本小题满分 12 分） 已知椭圆 2 2 1 2 2: 1( 0)x yC a ba b    的左、右顶点是双曲线 2 2 2 : 13 xC y  的顶点，且椭圆 1C 的上顶点 到双曲线 2C 的渐近线的距离为 3 2 ． （1）求椭圆 1C 的方程； （2）若直线l 与椭圆 1C 相交于不同的两点 1 2,M M ，与双曲线 2C 相交于不同的两点 1 2,Q Q ，且 1 2 5OQ OQ     （O 为坐标原点），求 1 2M M 的取值范围． 20．解析：（1）由题意可知 2 3a  ，椭圆 1C 的上顶点为(0, )b ，双曲线 2C 的渐近线方程为 3 0x y  ， 由点到直线的距离公式得， 3 3 2 2 b  ，得 1b  ，所以椭圆 1C 的方程为 2 2 13 x y  ．…………3 分 （2）易知直线l 的斜率存在，设直线l 的方程为 y kx m  ，将其代入 2 2 13 x y  ，消去 y 并整理得： 2 2 2(1 3 ) 6 3 3 0k x kmx m     ，因为直线l 与双曲线 2C 相交于不同的两点， 所以 2 2 2 2 2 2 2 2 1 3 0 1 3 0 36 4(1 3 )( 3 3) 0 1 3 k k k m k m m k                ① 设 1 1 1 2 2 2( , ), ( , )Q x y Q x y ，则有 2 1 2 1 22 2 6 3 3,1 3 1 3 km mx x x xk k      ． 又 2 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2( )( ) (1 ) ( ) 5OQ OQ x x y y x x kx m kx m k x x km x x m                ， 所以 2 2 2 2 2 2 2 1 [(1 )( 3 3) 6 (1 3 )] 51 3 k m k m m kk         ，得 2 21 9m k  ② 将 y kx m  代入 2 2 13 x y  ，消去 y 并整理得： 2 2 2(1 3 ) 6 3 3 0k x kmx m     ， 易知 2 2 2 2 2 236 4(1 3 )(3 3) 0 3 1k m k m k m         ， ③ 由①②③得， 2 10 9k ≤ ． ………………………………………6 分 设 1 3 3 2 4 4( , ), ( , )M x y M x y ，则 2 3 4 3 42 2 6 3 3,1 3 1 3 km mx x x xk k      ． 2 2 2 2 2 2 2 1 2 3 4 3 4 2 2 2 2 2 2 2 36 4(3 3)(1 3 )1 ( ) 4 1 (1 3 ) 4(3 3 9 )1 (1 3 ) k m m kM M k x x x x k k m kk k                  ………………8 分 将 2 21 9m k  代入，得 2 2 2 2 1 2 2 2 2 2 144 (1 )1 12(1 3 ) (1 3 ) k k kM M k k k      ，令 21 3t k  ，则 41, 3t     ， 则 22 2 2 2 2 2 2 1 (1 ) ( 1)( 2) 1 2 1 2 1 1 1 5, 1 0,3 (1 3 ) 9 9 9 4 8 72 t k k t tk k t t t t                                ， 所以 1 2 (0, 10]M M  ． ……………………………………………………………………12 分 21．（本小题满分 12 分） 已知函数 1( ) ln 1 xf x axx   ． （1）讨论 ( )f x 的单调性； （2）当 (0,1)x 时， 2 4 1 ax ax xe e x    ，求实数 a 的取值范围． 21．（1） 2 2 2 1 2 20, 1 1, ( ) , 1 11 1 1 x ax ax f x a xx x x                ，易知 ( ) 2f x a ≥ ． 当 2a ≤ 时， ( ) 0, ( )f x f x ≥ 在( 1,1) 上单调递增． 当 2a  时， 2 2( ) 0 1 1f x xa a         ， 2( ) 0 1 1f x x a         或 21 1xa   ． ( )f x 在 2 21 , 1a a        上单调递减，在 21, 1 a        ， 21 ,1a      上单调递增．……………5 分 （2）当 2a ≤ 时，由（1）知 ( )f x 在 ( 1,1) 上单调递增， ∴当 (0,1)x 时， ( ) (0) 0 ( )f x f f x    ，即 1 1ln , ln1 1 x xax axx x      ， 从而可得1 1,1 1 ax axx xe ex x     ， 2 1 1 4 1 1 1 ax ax x x xe e x x x          ． 当 2a  时，由（1）知 ( )f x 在 2 21 , 1a a        上单调递减， 当 20, 1x a       时， ( ) (0) 0 ( )f x f f x    ，即 1 1ln , ln1 1 x xax axx x      ， 从而可得1 1,1 1 ax axx xe ex x     ， 2 1 1 4 1 1 1 ax ax x x xe e x x x          ，不合题意，舍去． 综上所示，实数 a 的取值范围为( ,2] ．………………………………………………………………12 分 （二）选考题：共 10 分．请考生在第 22、23 题中任选一题作答．如果多做，则按所作的第一题计分． 22．【选修 4—4：坐标系与参数方程】（本小题满分 10 分） 以平面直角坐标系的原点为极点， x 轴的正半轴为极轴建立极坐标系，已知直线l 的参数方程是 3 2 1 2 x t m y t      （ 0,m t 为参数），曲线C 的极坐标方程为 2cos  ． （1）求直线l 的普通方程和曲线C 的直角坐标方程； （2）若直线l 与 x 轴交于点 P ，与曲线C 交于不同的两点 ,A B ，且 1PA PB  ，求实数 m 的值． 22．（1）由题意知，直线l 的参数方程是 3 2 1 2 x t m y t      （ 0,m t 为参数），消去参数t ，可得直线l 的普 通方程是 3x y m  ． 由 2cos  ，得 2 2 cos   ， 2 2 2 , cos ,x y x      曲线C 的直角坐标方程为 2 2 2x y x  ． ………………………………………………………………………………………………………………5 分 （2）把 3 2 1 2 x t m y t      代入 2 2 2x y x  ，得 2 2( 3 3) 2 0t m t m m     ． 则 2 2 23( 2 1) 4( 2 ) 2 3 ( 1)( 3) 0m m m m m m m m               ，又 0m  ， 0 3m   ． 设点 ,A B 对应的参数分别为 1 2,t t ，则 2 1 2 2t t m m  ， 2 1 2 , 2 1PA PB t t m m      ，解得 1 2m   或 1m  ． 又 0 3, 1 2m m     或 1m  ．……………………………………………………………………10 分 23．【选修 4—5：不等式选讲】（本小题满分 10 分） 设函数 ( )f x x a x a    ． （1）当 1a  时，解不等式 ( ) 4f x ≥ ； （2）若 ( ) 6f x ≥ 在 Rx 上恒成立，求实数 a 的取值范围． 23．解析：（1）当 1a  时，不等式 ( ) 4 1 1 4f x x x   ≥ ≥ ， 当 1x  时， ( ) 2 4f x x ≥ ，得 2x≥ ； 当 1 1x ≤ ≤ 时， ( ) 2 4f x   ，原不等式无解； 当 1x   时， ( ) 2 4f x x  ≥ ，解得 2x ≤ ． 综上所述，不等式 ( ) 4f x ≥ 的解集为 ( , 2] [2, )   ．……………………………………5 分 （2） ( ) ( ) ( ) 2f x x a x a x a x a a       ≥ ，所以 2 6a ≥ ，解得 3a≥ 或 3a ≤ ， 所以实数 a 的取值范围是( , 3] [3, )   ．……………………………………………………10 分