- 2021-04-20 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
初中数学8年级教案:第3讲 一次函数中的面积问题
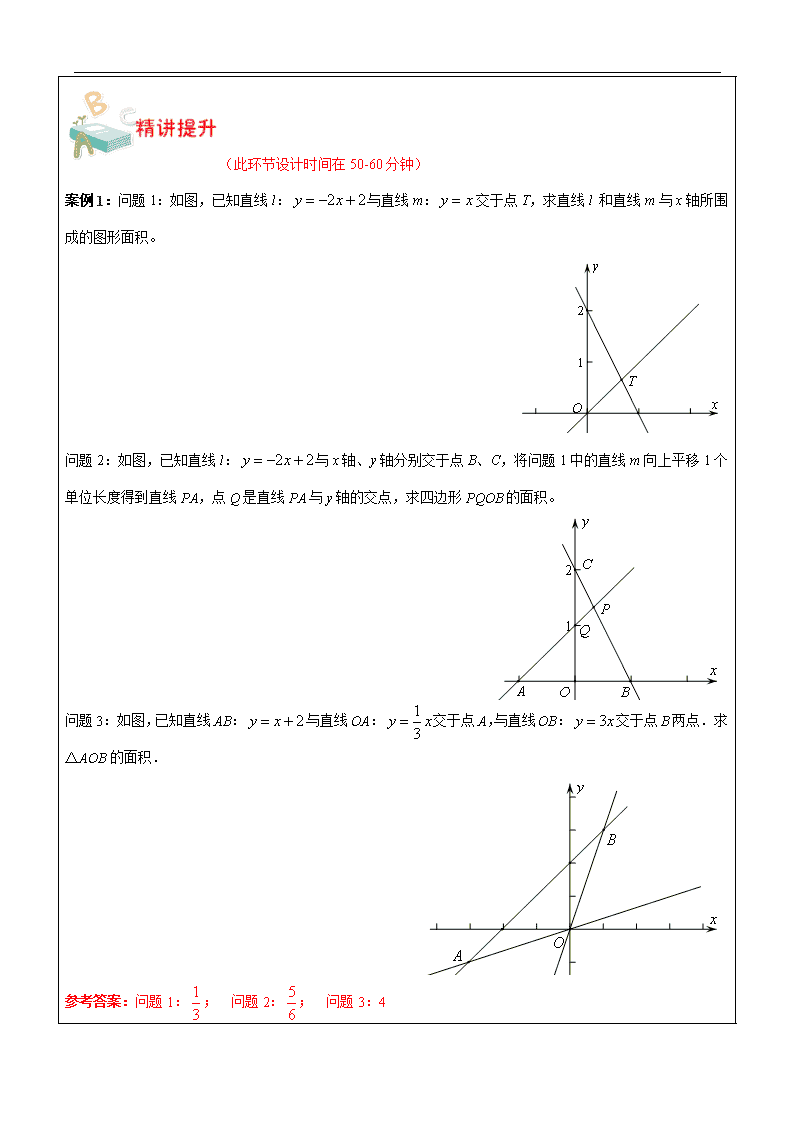
辅导教案 学员姓名: 学科教师: 年 级: 辅导科目: 授课日期 ××年××月××日 时 间 A / B / C / D / E / F段 主 题 一次函数中的面积问题 教学内容 1.能由一次函数的知识求有关图形的面积; 2.能由已知图形的面积解决一次函数的有关问题; 3.体会一次函数的有关面积问题的解决思路. (此环节设计时间在10—15分钟) 回顾上次课的预习思考内容,要求学生先画出一次函数的大致图形再解题. 1.直线与x轴相交于点 ,与y轴相交于点 ,与坐标轴围成的三角形面积为 . 2.一次函数的图像经过(3,5),(—4,—9),则此一次函数的解析式为 ,一次函数与坐标轴围成的三角形面积为 . 3.直线与直线相交于P,直线与x轴相交于点A ,直线 与x轴相交于点B ,交点P的坐标为 ,△ABP面积为 . 参考答案:1.(—1,0),(0,—1),; 2.,; 3.,,(1,1),; 归纳总结:一次函数与坐标轴围成的面积可以推到出相应公式: (此环节设计时间在50-60分钟) 案例1:问题1:如图,已知直线l:与直线m:交于点T,求直线l 和直线m与x轴所围成的图形面积。 问题2:如图,已知直线l:与x轴、y轴分别交于点B、C,将问题1中的直线m向上平移1个单位长度得到直线PA,点Q是直线PA与y轴的交点,求四边形PQOB的面积。 问题3:如图,已知直线AB:与直线OA:交于点A,与直线OB:交于点B两点.求△AOB的面积. 参考答案:问题1:; 问题2:; 问题3:4 例题2:已知直线的图像与x轴、y轴分别交于A、B两点,直线l经过原点,与线段AB交于点C,把△AOB的面积分为2:l两部分,求直线l的解析式. 参考答案: 解:由题意: ∴ ∴ ∴ 代入得, 设直线l的解析式: 代入得 ∴直线l的解析式 同理:,∴直线l的解析式 试一试:已知直线与x轴、y轴分别交于A点和B点,另一条直线经过点C(1,0),且把△AOB分成两部分。若△AOB被分成的两部分面积比为1:5,求k和b的值. 参考答案:或 此环节设计时间在30分钟左右(20分钟练习+10分钟互动讲解)。 1.如图,直线与x轴相交于点A,与直线相交于点P. (1)求点P的坐标. (2)请判断△OPA的形状并说明理由. 2.已知平面直角坐标系,直线 经过第一、二、三象限,与y轴交于点B,点A(2,t)在这条直线上,联结AO,△AOB的面积等于1. (1)求b的值; (2)如果反比例函数(k是常量,)的图像经过点A,求这个反比例函数的解析式. 3.如图,已知直线PA:与直线PB:交于点P. (1)用m、n表示出A、B、P点的坐标; (2)若点Q是直线PA与y轴的交点,且四边形PQOB的面积,AB=2,试求点P的坐标,并写出直线PA 与PB的解析式. 参考答案:1.(1)点P的坐标为; (2)△POA是等边三角形 2.(1); (2) 3.(1),,;(2)PA:,PB:. (此环节设计时间在5—10分钟内) 让学生回顾本节课所学的重点知识,以学生自我总结为主,学科教师引导为辅,为本次课做一个总结回顾 【巩固练习】 1.已知函数的图像过点(—1,—5)和(2,4),函数的图像与直线平行,且过点(—1,1). (1)求出这两个函数的解析式; (2)求这两个函数与轴所围成三角形的面积. 2.如图,直线与y轴交于点A,与直线交于点B,且直线与x轴交于点C,求△ABC的面积. 3.如图所示,直线的截距为6,该直线分别交x轴、y轴于E、F,点E的坐标为(-4,0). (1)求直线的表达式; (2)若点P(x,y)是该直线第二象限上的一个动点,PA⊥x轴,PB⊥y轴,垂足分别为点A、B,试求四边形OAPB的面积S与x的函数关系式,并写出自变量x的取值范围. 参考答案:1.(1),; (2); 2.4; 3.(1);(2) 【预习思考】 1.整式方程: ,这个方程叫做一元整式方程. 2.一元n次方程: ,这个方程叫做一元次方程. 3.一元高次方程: ,这样的方程统称为一元高次方程. 4.(1)二项方程: ,那么这样的方程就叫做二项方程. (2)二项方程的一般形式为: . (3)二项方程根的情况:当n为奇数时, . 当n为偶数时, ; 5.下面四个方程中是整式方程的是( ). A. B. C. D.. 6.下面四个关于的方程中,次数和另外三个不同的是( ). A. B. C. D.. 7.下列方程中,是二项方程的是( ) A. ; B.; C.; D. .查看更多