- 2021-04-20 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学理卷·2018届陕西省黄陵中学高新部高二下学期第四学月考试(2017-06)
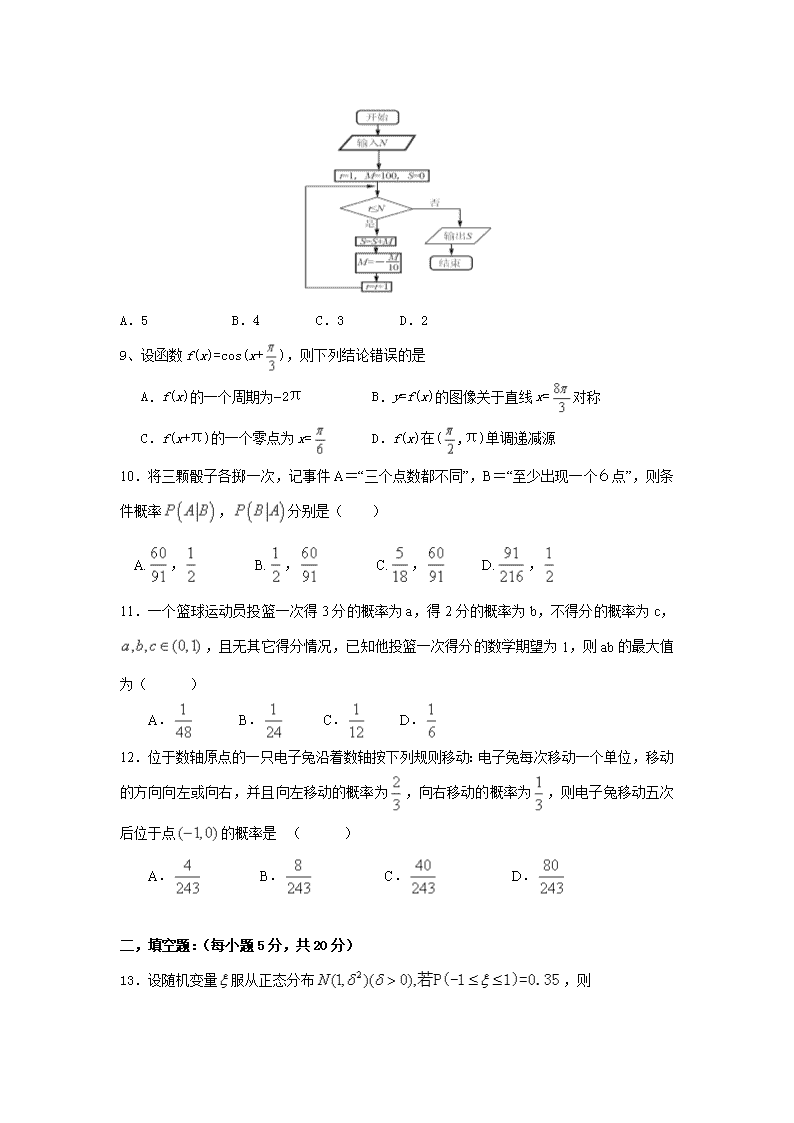
高新部第四次月考理科数学试题 一,选择题:(每小题5分,共60分) 1.下列说法中正确的是( ) A.一个命题的逆命题为真,则它的逆否命题一定为真 B.“”与“ ”不等价 C.“,则全为”的逆否命题是“若全不为, 则” D.一个命题的否命题为真,则它的逆命题一定为真 2.若命题“”为假,且“”为假,则( ) A.或为假 B.假 C.真 D.不能判断的真假 3.设,则是 的( ) A.充分但不必要条件 B.必要但不充分条件 C.充要条件 D.既不充分也不必要条件 4.给出下列三个命题: ①“若,则”为假命题; ②若∧为假命题,则,均为假命题; ③命题:,则.其中正确的个数是( ) A.0 B.1 C.2 D.3 5.一个篮球运动员投篮一次得3分的概率为,得2分的概率为,不得分的概率为,,已知他投篮一次得分的数学期望是2,则的最小值为( ) A. B. C. D. 6.展开式中常数项为( ) A. B. C. D. 7、某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为 A.10 B.12 C.14 D.16 8、执行下面的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为 A.5 B.4 C.3 D.2 9、设函数f(x)=cos(x+),则下列结论错误的是 A.f(x)的一个周期为−2π B.y=f(x)的图像关于直线x=对称 C.f(x+π)的一个零点为x= D.f(x)在(,π)单调递减源 10.将三颗骰子各掷一次,记事件A=“三个点数都不同”,B=“至少出现一个6点”,则条件概率,分别是( ) A., B., C., D., 11.一个篮球运动员投篮一次得3分的概率为a,得2分的概率为b,不得分的概率为c,,且无其它得分情况,已知他投篮一次得分的数学期望为1,则ab的最大值为( ) A. B. C. D. 12.位于数轴原点的一只电子兔沿着数轴按下列规则移动:电子兔每次移动一个单位,移动的方向向左或向右,并且向左移动的概率为,向右移动的概率为,则电子兔移动五次后位于点的概率是 ( ) A. B. C. D. 二,填空题:(每小题5分,共20分) 13.设随机变量服从正态分布,则 . 14、若tan,则tan= . 15、.某工厂生产甲、乙、丙、丁四种不同型号的产品,产量分别为200,400,300,100件,为检验产品的质量,现用分层抽样的方法从以上所有的产品中抽取60件进行检验,则应从丙种型号的产品中抽取 件. 16.若函数定义域为,值域为,则的值为 _. 三,解答题:(每题10分,共40分) 17. 在直角坐标系中,以坐标原点为极点,轴正半轴为极轴建立极坐标系,直线的极坐标方程为: ,曲线的极坐标方程为: (1)求和的直角坐标方程; (2)求曲线上的点到直线的距离的最大值. 18.已知椭圆,直线 恒过的定点F为椭圆的一个焦点,且椭圆上的点到焦点F的最大距离为3. (1)求椭圆C的方程; (2)若直线MN为垂直于x轴的动弦,且M,N在椭圆C上,定点T(4,0),直线MF与直线NT交于点S. ①证:点S恒在椭圆C上; ②求△MST面积的最大值. 19.甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为与p,且乙投球2次均未命中的概率为. (1) 求乙投球的命中率; (2) 求甲投球2次,至少命中1次的概率; (1) 若甲、乙两人各投球2次,求共命中2次的概率. 20.某彩票的号码形如“”(其中,)。现从0~9这十个数字中每次取出一个数字,放回后再取下一个数字,取5次,依次按序排成一行成为一等奖号码。若彩票上的号码与一等奖号码恰有4个连续的数字相同(包括数字顺序相同)则为二等奖号码,恰有3个连续的数字相同(包括数字顺序相同)则为三等奖号码,其它为不中奖号码。 (1)求某人买一张彩票中一等奖的概率; (2)若一等奖奖金1000元,二等奖奖金500元,三等奖奖金100元,求某人买一张彩票获得奖金数X(元)的概率分布及其数学期望; (3)某人买了3张彩票,恰有1张获奖的概率是恰有2张获奖的概率的多少倍? 一,选择题,1-5:DBABD 6-10:BBDDA 11-12:BD 二,填空题,13.【答案】 0.15 14..15. 18.16.【答案】 三,解答题: 17.试题解析:(1)的方程为 的直角坐标方程为: (2) 18.②直线MS过点F(1,0),设其方程为,,,联立, 得:,∴,. .令, 则.∵在上是增函数,∴的最小值为10. ∴. ...... 19.(1)设“甲投一次球命中”为事件A,“乙投一次球命中”为事件B [1-P(B)]2=(1-p)2=1/16,p=3/4 (2)1-P()=3/4 (3) 20.解:(1)某人买一张彩票中一等奖的概率为; (2) 某人买一张彩票中二奖的概率为 某人买一张彩票中三奖的概率为 某人买一张彩票得奖金数X(元)的概率分布为: X 1000 500 100 0 P 则 (3) 购买彩票获奖的概率为, 某人买了3张彩票,恰有1张获奖的概率是, 恰有2张获奖的概率是, 此时. 查看更多