河北省张家口市2020届高三上学期入学摸底联合考试数学（理）试题

河北省张家口市2020届高三上学期入学摸底联合考试数学（理）试题

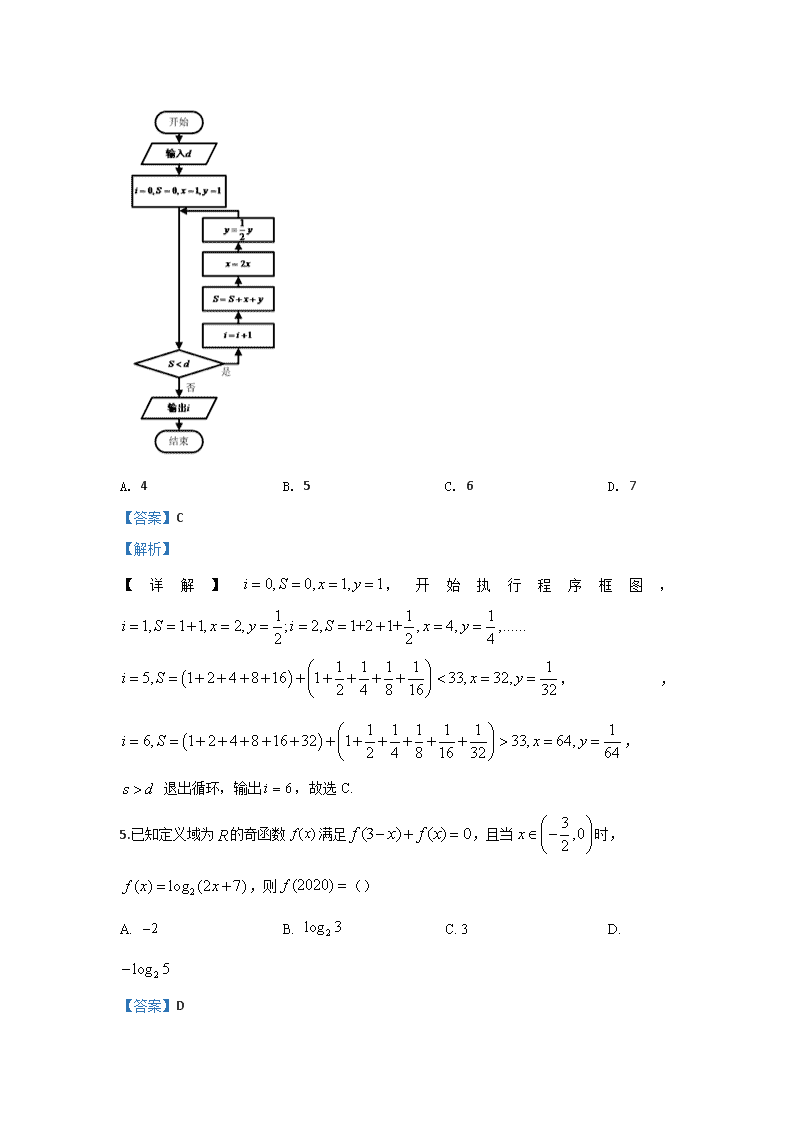
全国卷高三入学摸底联合考试 理科数学 第Ⅰ卷（选择题共60分）‎ 一、选择题（本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1.设函数的定义域，函数的定义域为，则（）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据幂函数及对数函数定义域的求法，即可求得和，即可求得．‎ ‎【详解】解：由，解得：，则函数的定义域，‎ 由对数函数的定义域可知：，解得：，则函数的定义域，‎ 则，‎ 故选C．‎ ‎【点睛】本题考查函数定义的求法，交集及其运算，考查计算能力，属于基础题．‎ ‎2.设，则 A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ 分析：利用复数的除法运算法则：分子、分母同乘以分母的共轭复数，化简复数，然后求解复数的模.‎ 详解：‎ ‎，‎ 则，故选c.‎ 点睛：复数是高考中的必考知识，主要考查复数的概念及复数的运算．要注意对实部、虚部的理解，掌握纯虚数、共轭复数这些重要概念，复数的运算主要考查除法运算，通过分母实数化转化为复数的乘法，运算时特别要注意多项式相乘后的化简，防止简单问题出错，造成不必要的失分.‎ ‎3.若f(x)=ln(x2-2ax+1+a)在区间上递减,则实数的取值范围为（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 由外函数对数函数是增函数，可得要使函数在上递减，需内函数二次函数的对称轴大于等于1，且内函数在上的最小值大于0，由此联立不等式组求解．‎ ‎【详解】解：令，其对称轴方程为，‎ 外函数对数函数是增函数，‎ 要使函数在上递减，‎ 则，即：．‎ 实数的取值范围是．‎ 故选：．‎ ‎【点睛】本题主要考查了复合函数的单调性以及单调区间的求法．对应复合函数的单调性，一要注意先确定函数的定义域，二要利用复合函数与内层函数和外层函数单调性之间的关系进行判断，判断的依据是“同增异减”，是中档题．‎ ‎4.《九章算术》中的“两鼠穿墙”问题为“今有垣厚五尺，两鼠对穿，大鼠日一尺，小鼠也日一尺，大鼠日自倍，小鼠日自半，问何日相逢？”可用如图所示的程序框图解决此类问题.现执行该程序框图，输入的的值为33，则输出的的值为 A. 4 B. ‎5 ‎C. 6 D. 7‎ ‎【答案】C ‎【解析】‎ ‎【详解】，开始执行程序框图，，，， 退出循环，输出，故选C.‎ ‎5.已知定义域为的奇函数满足，且当时，，则（）‎ A. B. C. 3 D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 由题意利用函数奇偶性求得的周期为3，再利用函数的周期性求得的值．‎ ‎【详解】解：已知定义域为的奇函数满足，‎ ‎，的周期为3.‎ 时，，‎ ‎,‎ 故选D．‎ ‎【点睛】本题主要考查函数奇偶性和周期性，函数值的求法，属于基础题．‎ ‎6.已知小张每次射击命中十环的概率都为40%，现采用随机模拟的方法估计小张三次射击恰有两次命中十环的概率，先由计算器产生0到9之间取整数值的随机数，指定2，4，6，8表示命中十环，0，1，3，5，7，9表示未命中十环，再以每三个随机数为一组，代表三次射击的结果，经随机模拟产生了如下20组随机数：‎ ‎321 421 292 925 274 632 800 478 598 663 531 297 396 ‎ ‎021 506 318 230 113 507 965‎ 据此估计，小张三次射击恰有两次命中十环的概率为（）‎ A. 0.25 ‎B. ‎0.30 ‎C. 0.35 D. 0.40‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 由题意知模拟三次射击的结果，经随机模拟产生了如下20组随机数，在20组随机数中表示三次射击恰有两次命中十环的有可以通过列举得到共6组随机数，根据概率公式，得到结果．‎ ‎【详解】解：由题意知模拟三次射击的结果，经随机模拟产生了如下20组随机数，‎ 在20组随机数中表示三次射击恰有两次命中的有：421、292、274、632、478、663，‎ 共6组随机数，∴所求概率为，故选B．‎ ‎【点睛】‎ 本题考查模拟方法估计概率，是一个基础题，解这种题目的主要依据是等可能事件的概率，注意列举法在本题的应用．‎ ‎7.若非零向量，满足，且，则与的夹角为（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 根据向量垂直的等价条件以及向量数量积的应用进行求解即可．‎ ‎【详解】∵（﹣）⊥（3+2），‎ ‎∴（﹣）•（3+2）=0，‎ 即32﹣22﹣•=0，‎ 即•=32﹣22=2，‎ ‎∴cos＜，＞===，‎ 即＜，＞=，‎ 故选A．‎ ‎【点睛】本题主要考查向量夹角的求解，利用向量数量积的应用以及向量垂直的等价条件是解决本题的关键．‎ ‎8.记，则的值为  ‎ A. 1 B. ‎2 ‎C. 129 D. 2188‎ ‎【答案】C ‎【解析】‎ ‎【详解】中，令，得 ‎.‎ ‎∵展开式中 ‎∴‎ 故选C.‎ 点睛：二项式通项与展开式的应用：‎ ‎(1)通项的应用：利用二项展开式的通项可求指定项或指定项的系数等.‎ ‎(2)展开式的应用：‎ ‎①可求解与二项式系数有关的求值，常采用赋值法.‎ ‎②可证明整除问题(或求余数).关键是要合理地构造二项式，并将它展开进行分析判断.‎ ‎③有关组合式的求值证明，常采用构造法.‎ ‎9.已知数列是各项均为正数的等比数列，，设其前项和为，若，，成等差数列，则（）‎ A. 682 B. ‎683 ‎C. 684 D. 685‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 由，且，，成等差数列，求出公比，由此能求出．‎ ‎【详解】解：∵各项均为正数的等比数列的前项和为，‎ ‎，且，，成等差数列，‎ ‎，且，‎ 解得，，故选A．‎ ‎【点睛】本题考查等比数列的前5项和的求法，考查等差数列、等比数列的性质等基础知识、考查运算求解能力，考查函数与方程思想，是基础题．‎ ‎10.已知椭圆的右焦点为．短轴的一个端点为，直线 交椭圆于两点．若，点到直线的距离不小于，则椭圆的离心率的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ 试题分析：设是椭圆的左焦点，由于直线过原点，因此两点关于原点对称，从而是平行四边形，所以，即，，设，则，所以，，即，又，所以，．故选A．‎ 考点：椭圆的几何性质．‎ ‎【名师点睛】本题考查椭圆的离心率的范围，因此要求得关系或范围，解题的关键是利用对称性得出就是，从而得，于是只有由点到直线的距离得出的范围，就得出的取值范围，从而得出结论．在涉及到椭圆上的点到焦点的距离时，需要联想到椭圆的定义．‎ ‎【此处有视频，请去附件查看】‎ ‎11.已知，设函数的最大值为，最小值为，那么（）‎ A. 2020 B. ‎2019 ‎C. 4040 D. 4039‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 通过分离分子可得，计算可得，利用函数的单调性计算可得结果．‎ ‎【详解】解：，‎ 又是上的增函数，，故选D．‎ ‎【点睛】本题考查函数的单调性的判断和运用，注意解题方法的积累，考查运算能力，属于中档题．‎ ‎12.已知三棱锥中，平面，且，.则该三棱锥的外接球的体积为( )‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【详解】‎ ‎∵，，∴ 是以 为斜边的直角三角形， 其外接圆半径 ，‎ 则三棱锥外接球即为以为底面，以 为高的三棱柱的外接球， ∴三棱锥外接球的半径满足 ‎ 故三棱锥外接球的体积 ‎ 故选D.‎ ‎【点睛】本题考查的知识点是球内接多面体，其中根据已知求出球的半径是解答的关键．‎ 第Ⅱ卷（非选择题共90分）‎ 二、填空题（本题共4小题，每小题5分，共20分）‎ ‎13.已知函数的导函数为，且满足，则______.‎ ‎【答案】.‎ ‎【解析】‎ ‎【分析】‎ 对函数的解析式求导，得到其导函数，把代入导函数中，列出关于的方程，进而得到的值，确定出函数的解析式，把代入解析式，即可求出的值 ‎【详解】解：求导得：，令，得，解得：‎ ‎∴，，故答案为-2．‎ ‎【点睛】此题考查了导数的运算，以及函数的值．运用求导法则得出函数的导函数，求出常数的值，从而确定出函数的解析式是解本题的关键．‎ ‎14.设，，且，则当取最小值时，______.‎ ‎【答案】12‎ ‎【解析】‎ ‎【分析】‎ 当取最小值时，取最小值，变形可得，由基本不等式和等号成立的条件可得答案．‎ ‎【详解】解析：∵，，∴当取最小值时，取得最小值，‎ ‎∵，又，‎ ‎∴，∴，‎ ‎∴，‎ 当且仅当，即时取等号，‎ ‎∴当取最小值时，，，‎ ‎∴，∴.‎ ‎【点睛】本题考查基本不等式求最值，变形为可用基本不等式的形式是解决问题的关键，属中档题．‎ ‎15.某商店为调查进店顾客的消费水平，调整营销思路，统计了一个月来进店的2000名顾客的消费金额（单位：元），并从中随机抽取了100名顾客的消费金额按，，，，进行统计，得到如图所示的频率分布直方图.已知，，成等差数列，则该商店这一个月来消费金额超过150元的顾客数量约为______.‎ ‎【答案】600‎ ‎【解析】‎ ‎【分析】‎ 先根据频率分布直方图求出的值，然后利用等差数列的性质求出，进而得到消费金额超过150元的频率，用其估计总体即可．‎ ‎【详解】，‎ 又由频率分布直方图可得，‎ ‎，故消费金额超过150元的频率为，故该商店这一个月来消费金额超过150元的顾客数量约为，故答案为600.‎ ‎【点睛】本题主要考查频率分布直方图中的基本运算及等差数列的基本性质，是一道基础题．‎ ‎16.已知为数列的前项和，，若，则__________．‎ ‎【答案】‎ ‎【解析】‎ ‎【详解】因为，所以数列为等比数列 所以， ‎ 又，‎ 则 ，故答案为.‎ 点睛：裂项相消法是指将数列的通项分成两个式子的代数差的形式，然后通过累加抵消中间若干项的方法，裂项相消法适用于形如 (其中是各项均不为零的等差数列，c为常数)的数列. 裂项相消法求和，常见的有相邻两项的裂项求和(如本例)，还有一类隔一项的裂项求和，如或.‎ 三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤）‎ ‎17.在中，角、、所对的边分别为、、，且满足 ‎.‎ ‎（1）求角的值；‎ ‎（2）若且，求的取值范围.‎ ‎【答案】（1）或（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）利用三角函数恒等变换的应用化简已知可解得：，结合为的内角，可得的值．（2）由，由（1）可得，又，‎ 由正弦定理可得：，从而利用三角函数恒等变换应用可得：‎ ‎，结合，可得取值范围．‎ ‎【详解】解：（1）由已知得，化简得，‎ 因为为的内角，所以，故或.‎ ‎（2）因为，所以.由正弦定理得，得，，‎ 故＝.‎ 因为，所以，则，所以 ‎．‎ ‎【点睛】本题主要考查了三角函数恒等变换的应用，考查了正弦定理，正弦函数的图象和性质在解三角形中的应用，属于中档题．‎ ‎18.如图①，正方形的边长为4，，，把四边形沿折起，使得平面，是的中点，如图②‎ ‎（1）求证：平面；‎ ‎（2）求二面角的余弦值.‎ ‎【答案】（1）详见解析（2）‎ ‎【解析】‎ ‎【分析】‎ 首先结合已知底面，所以有，再结合菱形的性质即可得到，那么（1）便不难求证了．对于（2）首先建立如图所示的空间直角坐标系，分析可知，为平面的一个法向量，再求出平面的法向量，然后根据进行求解即可．‎ ‎【详解】解：（1）证明：连接，因为，底面，‎ 所以底面，又底面，所以，‎ 因为，所以四边形为菱形，所以，‎ 又，平面，平面，所以平面.‎ ‎（2）由（1）知四边形菱形，，，‎ 设，所以，，‎ 以为坐标原点，建立如图所示的空间直角坐标系，‎ 则，，，，，，‎ 所以，，‎ 设平面的法向量为，‎ 则所以令，则，，‎ 即平面一个法向量为，‎ 易知平面的一个法向量为，‎ 设二面角的大小为，由图易知，‎ 所以.‎ ‎【点睛】本题考查了直线与平面垂直的判定．熟记判定定理即可证得结论，另外空间向量法求面面角，要关注是否有一个面的法向量可以直接观察出来，就不用专门取求了，还要提高计算的准确性，此题属于中档题．‎ ‎19.中国农业银行开始为全国农行ATM机安装刷脸取款系统.某农行营业点为调查居民对刷脸取款知识的了解情况,制作了刷脸取款知识有奖调查问卷,发放给2018年度该行的所有客户,并从参与调查且年龄(单位:岁)在[25,55]内的客户中随机抽取100名给予物质奖励,再从中选出一名客户参加幸运大抽奖.调查结果按年龄分成6组,制作成如下的频数分布表和女客户的年龄茎叶图,其中a∶b∶c=2∶4∶5.‎ 年龄/岁 ‎[25,30)‎ ‎[30,35)‎ ‎[35,40)‎ ‎[40,45)‎ ‎[45,50)‎ ‎[50,55]‎ 频数/人 ‎5‎ a b c ‎15‎ ‎25‎ 女客户的年龄茎叶图 幸运大抽奖方案如下:客户最多有两次抽奖机会,每次抽奖的中奖率均为,第一次抽奖,若未中奖,则抽奖结束.若中奖,则通过抛掷一枚质地均匀的硬币,决定是否继续进行第二次抽奖.规定:抛出的硬币,若反面朝上,则客户获得5000元奖金,不进行第二次抽奖;若正面朝上,客户需进行第二次抽奖,且在第二次抽奖中,如果中奖,则获得奖金10000元,如果未中奖,则所获得的奖金为0元.‎ ‎(1)求a,b,c的值,若分别从男、女客户中随机选取1人,求这2人的年龄均在[40,45)内的概率;‎ ‎(2)若参加幸运大抽奖的客户所获奖金(单位:元)用X表示,求X的分布列与数学期望E(X).‎ ‎【答案】（1），概率为；（2）见解析 ‎【解析】‎ ‎【分析】‎ ‎（1）根据解方程组，求得的值.先根据茎叶图求得每组内女客户的人数，进而求得每组男客户的人数，然后根据相互独立事件概率计算公式，求得所求的概率.（2）先求得所有可能取值为.然后根据分类和分步计算原理求得对应的概率，由此求得分布列和数学期望.‎ ‎【详解】(1)由频数分布表知,a+b+c=100-45=55.‎ 因a∶b∶c=2∶4∶5,‎ 所以a=×55=10,b=×55=20,c=×55=25,由茎叶图可知年龄在[25,30)内的女客户有2人,年龄在[30,35)内的女客户有4人,年龄在[35,40)内的女客户有8人,年龄在[40,45)内的女客户有10人,年龄在[45,50)内的女客户有6人,年龄在[50,55]内的女客户有10人,‎ 故年龄在[40,45)内的男客户有15人,在100名客户中,男客户有60人,女客户有40人,所以从男客户中随机选取1人,年龄恰在[40,45)内的概率P1=,‎ 从女客户中随机选取1人,年龄恰在[40,45)内的概率P2=,‎ 则分别从男、女客户中随机选取1人,这2人的年龄均在[40,45)内的概率P=P1×P2=.‎ ‎(2)由题意可知,X的所有可能取值为0,5000,10000,则 P(X=0)=,‎ P(X=5000)=,‎ P(X=10000)=.‎ X的分布列为 X ‎0‎ ‎5 000‎ ‎10 000‎ P E(X)=0×+5000×+10000×=5200(元).‎ ‎【点睛】本小题主要考查茎叶图的识别，考查数据分析与处理能力，考查相互独立事件概率计算方法，考查分布列和数学期望的求法，属于中档题.‎ ‎20.已知过点的直线交抛物线于两点，直线交轴于点．‎ ‎（1）设直线的斜率分别为，求的值；‎ ‎（2）点为抛物线上异于的任意一点，直线交直线于两点，，求抛物线的方程．‎ ‎【答案】（1）；（2）．‎ ‎【解析】‎ ‎【分析】‎ ‎（1）首先设出直线的方程为，且，然后联立直线与抛物线的方程并整理得到一元二次方程，再由韦达定理可得：，最后代入中，并化简整理即可得出所求的结果；（2）首先设出点，即可求出直线的方程，进而可求出，，再由已知条件即可得出等式，进而得出参数的值，即可得出所求的抛物线的方程．‎ ‎【详解】（1）设直线的方程为：，点，联立方程组，得，所以 所以 ‎.‎ ‎（2）设点，直线当时，，‎ 同理，‎ 因为，，‎ 即，，‎ 所以，所以抛物线的方程为．‎ 考点：1、抛物线的标准方程；2、抛物线的简单几何性质；3‎ ‎、直线与抛物线的相交的综合问题．‎ ‎21.已知函数.‎ ‎（1）当时，求曲线在处的切线方程；‎ ‎（2）若函数在区间上的最小值为0，求的值.‎ ‎【答案】（1）（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）由求导公式求出，由导数的几何意义求出切线的斜率，利用点斜式方程求出切线的方程；‎ ‎（2）对进行分类讨论，当时，，不符合题意，当时，求出以及函数的单调区间，再对临界点与1的关系进行分类讨论，分别求出的最小值，结合条件求出的值；‎ ‎【详解】解：（1）当时，，，‎ 所求切线的斜率，又.‎ 所以曲线在处的切线方程为 ‎（2）当时，函数，不符合题意．‎ 当时，，令，得，‎ 所以当时，，函数单调递减 当时，，函数单调递增．‎ ‎①当，即时，的最小值为．‎ 解，得，符合题意．‎ ‎②当，即时，的最小值为．‎ 解，得，不符合题意．‎ 综上，．‎ ‎【点睛】本题考查导数的几何意义，利用导数研究函数的单调性、最值，恒成立问题的转化，以及分类讨论和转化思想，属于中档题．‎ 请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分.‎ ‎22.在直角坐标系中，以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为．‎ ‎（1）为曲线上的动点，点在线段上，且满足，求点的轨迹的直角坐标方程；‎ ‎（2）设点的极坐标为，点在曲线上，求面积的最大值．‎ ‎【答案】（1）；（2）‎ ‎【解析】‎ ‎【详解】试题分析：（1）设出P的极坐标，然后由题意得出极坐标方程，最后转化为直角坐标方程为；‎ ‎（2）利用（1）中的结论，设出点的极坐标，然后结合面积公式得到面积的三角函数，结合三角函数的性质可得面积的最大值为.‎ 试题解析：解：（1）设P的极坐标为（）（＞0），M的极坐标为（）由题设知 ‎|OP|=，=.‎ 由|OP|=16得的极坐标方程 因此的直角坐标方程为.‎ ‎（2）设点B的极坐标为 （）.由题设知|OA|=2，，于是△OAB面积 当时， S取得最大值.‎ 所以△OAB面积的最大值为.‎ 点睛:本题考查了极坐标方程的求法及应用，重点考查了转化与化归能力.在求曲线交点、距离、线段长等几何问题时，求解的一般方法是将其化为普通方程和直角坐标方程后求解，或者直接利用极坐标的几何意义求解.要结合题目本身特点，确定选择何种方程.‎ ‎23.已知函数，．‎ ‎（1）当时，求不等式的解集；‎ ‎（2）若不等式的解集包含[–1，1]，求的取值范围．‎ ‎【答案】（1）；（2）．‎ ‎【解析】‎ ‎【详解】试题分析：（1）分，，三种情况解不等式；（2）的解集包含，等价于当时，所以且，从而可得．‎ 试题解析：（1）当时，不等式等价于.①‎ 当时，①式化为，无解；‎ 当时，①式化为，从而；‎ 当时，①式化为，从而.‎ 所以的解集为.‎ ‎（2）当时，.‎ 所以的解集包含，等价于当时.‎ 又在的最小值必为与之一，所以且，得 ‎.‎ 所以的取值范围为.‎ 点睛:形如(或)型的不等式主要有两种解法：‎ ‎(1)分段讨论法：利用绝对值号内式子对应方程的根，将数轴分为，， (此处设)三个部分，将每部分去掉绝对值号并分别列出对应的不等式求解，然后取各个不等式解集的并集．‎ ‎(2)图像法：作出函数和的图像，结合图像求解．‎