- 2021-04-20 发布 |
- 37.5 KB |
- 5页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高中数学(人教版必修2)配套练习 第二章2.2.4 平面与平面平行的性质
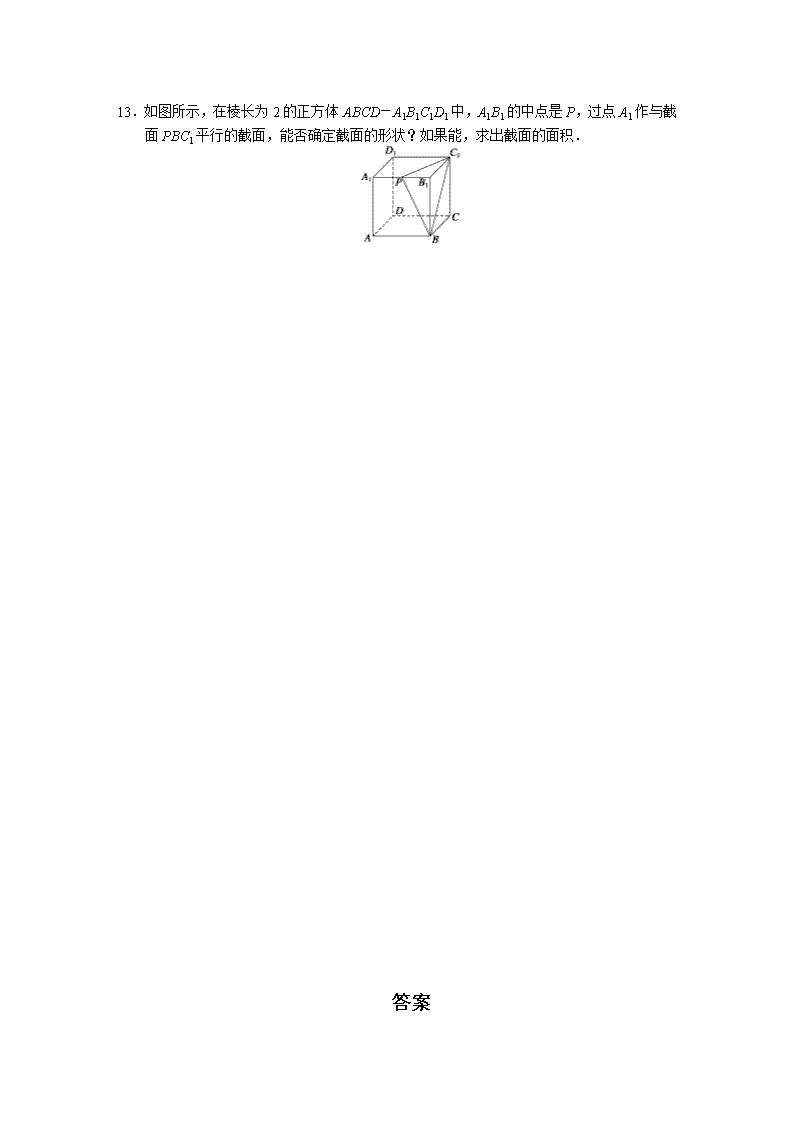
2.2.4 平面与平面平行的性质 一、基础过关 1.已知平面α∥平面β,过平面α内的一条直线 a 的平面γ,与平面β相交,交线为直线 b,则 a、b 的位置关系是 ( ) A.平行 B.相交 C.异面 D.不确定 2.已知 a、b 表示直线,α、β表示平面,下列推理正确的是 ( ) A.α∩β=a,b⊂α⇒a∥b B.α∩β=a,a∥b⇒b∥α且 b∥β C.a∥β,b∥β,a⊂α,b⊂α⇒α∥β D.α∥β,α∩γ=a,β∩γ=b⇒a∥b 3. 如图所示,P 是三角形 ABC 所在平面外一点,平面α∥平面 ABC,α分别交 线 段 PA 、 PB 、 PC 于 A′ 、 B′ 、 C′ , 若 PA′∶AA′ = 2∶3 , 则 S△A′B′C′∶S△ABC 等于 ( ) A.2∶25 B.4∶25 C.2∶5 D.4∶5 4.α,β,γ为三个不重合的平面,a,b,c 为三条不同的直线,则有下列命题,不正确的是 ( ) ① a∥c b∥c ⇒a∥b; ② a∥γ b∥γ ⇒a∥b; ③ α∥c β∥c ⇒α∥β; ④ α∥γ β∥γ ⇒α∥β; ⑤ α∥c a∥c ⇒α∥a; ⑥ α∥γ a∥γ ⇒a∥α. A.④⑥ B.②③⑥ C.②③⑤⑥ D.②③ 5.分别在两个平行平面的两个三角形.(填“相似”“全等”) (1)若对应顶点的连线共点,那么这两个三角形具有______关系; (2)若对应顶点的连线互相平行,那么这两个三角形具有________关系. 6.已知平面α∥β∥γ,两条直线 l、m 分别与平面α、β、γ相交于点 A、B、C 与 D、E、F. 已知 AB=6,DE DF =2 5 ,则 AC=______. 7.如图,在三棱柱 ABC-A1B1C1 中,M 是 A1C1 的中点,平面 AB1M∥平面 BC1N,AC∩平面 BC1N=N. 求证:N 为 AC 的中点. 8. 如图所示,在底面是平行四边形的四棱锥 P-ABCD 中,点 E 在 PD 上,且 PE∶ED=2∶1, 在棱 PC 上是否存在一点 F,使 BF∥平面 AEC?并证明你的结论. 二、能力提升 9.设α∥β,A∈α,B∈β,C 是 AB 的中点,当 A、B 分别在平面α、β内运动时,得到无数 个 AB 的中点 C,那么所有的动点 C ( ) A.不共面 B.当且仅当 A、B 分别在两条直线上移动时才共面 C.当且仅当 A、B 分别在两条给定的异面直线上移动时才共面 D.不论 A、B 如何移动,都共面 10.已知平面α∥平面β,P 是α,β外一点,过点 P 的直线 m 与α,β分别交于点 A,C,过点 P 的直线 n 与α,β分别交于点 B,D,且 PA=6,AC=9,PD=8,则 BD 的长为( ) A.16 B.24 或24 5 C.14 D.20 11.对于不重合的两个平面α与β,给定下列条件:①存在平面γ,使得α、β都垂直于γ;②存 在平面γ,使α、β都平行于γ;③α内有不共线的三点到β的距离相等;④存在异面直线 l, m,使得 l∥α,l∥β,m∥α,m∥β.其中可以判断两个平面α与β平行的条件有________ 个. 12. 如图所示,平面α∥平面β,△ABC、△A′B′C′分别在α、β内,线段 AA′、BB′、CC′ 共点于 O,O 在α、β之间,若 AB=2,AC=1,∠BAC=90°,OA∶OA′=3∶2. 求△A′B′C′的面积. 三、探究与拓展 13.如图所示,在棱长为 2 的正方体 ABCD-A1B1C1D1 中,A1B1 的中点是 P,过点 A1 作与截 面 PBC1 平行的截面,能否确定截面的形状?如果能,求出截面的面积. 答案 1.A 2.D 3.B 4.C 5.(1)相似 (2)全等 6.15 7.证明 ∵平面 AB1M∥平面 BC1N, 平面 ACC1A1∩平面 AB1M=AM, 平面 BC1N∩平面 ACC1A1=C1N, ∴C1N∥AM,又 AC∥A1C1, ∴四边形 ANC1M 为平行四边形, ∴AN=C1M=1 2A1C1=1 2AC, ∴N 为 AC 的中点. 8. 解 当 F 是棱 PC 的中点时,BF∥平面 AEC, 证明如下: 取 PE 的中点 M,连接 FM,则 FM∥CE,① 由 EM=1 2PE=ED,知 E 是 MD 的中点,设 BD∩AC=O, 则 O 为 BD 的中点,连接 OE,则 BM∥OE,② 由①②可知,平面 BFM∥平面 AEC,又 BF⊂平面 BFM, ∴BF∥平面 AEC. 9.D 10.B 11.2 12.解 相交直线 AA′,BB′所在平面和两平行平面α、β分别相交于 AB、A′B′, 由面面平行的性质定理可得 AB∥A′B′. 同理相交直线 BB′、CC′确定的平面和平行平面α、β分别相交于 BC、B′C′,从而 BC∥B′C′.同理易证 AC∥A′C′. ∴∠BAC 与∠B′A′C′的两边对应平行且方向相反. ∴∠BAC=∠B′A′C′. 同理∠ABC=∠A′B′C′,∠BCA=∠B′C′A′. ∴△ABC 与△A′B′C′的三内角分别相等, ∴△ABC∽△A′B′C′,∵AB∥A′B′,AA′∩BB′=O, ∴在平面 ABA′B′中,△AOB∽△A′OB′. ∴A′B′ AB =OA′ OA =2 3.而 S△ABC=1 2AB·AC=1 2 ×2×1=1. ∴S△A′B′C′ S△ABC =(A′B′ AB )2, ∴S△A′B′C′=4 9S△ABC=4 9 ×1=4 9. 13.解 能.取 AB,C1D1 的中点 M,N,连接 A1M,MC,CN,NA1, ∵A1N∥PC1 且 A1N=PC1,PC1∥MC,PC1=MC, ∴四边形 A1MCN 是平行四边形, 又∵A1N∥PC1,A1M∥BP,A1N∩A1M=A1,C1P∩PB=P, ∴平面 A1MCN∥平面 PBC1, 因此,过点 A1 与截面 PBC1 平行的截面是平行四边形. 连接 MN,作 A1H⊥MN 于点 H, ∵A1M=A1N= 5, MN=BC1=2 2, ∴A1H= 3. ∴S△A1MN=1 2 ×2 2× 3= 6. 故 S▱A1MCN=2S△A1MN=2 6.查看更多