中心对称（2）　　教案

中心对称（2）　　教案

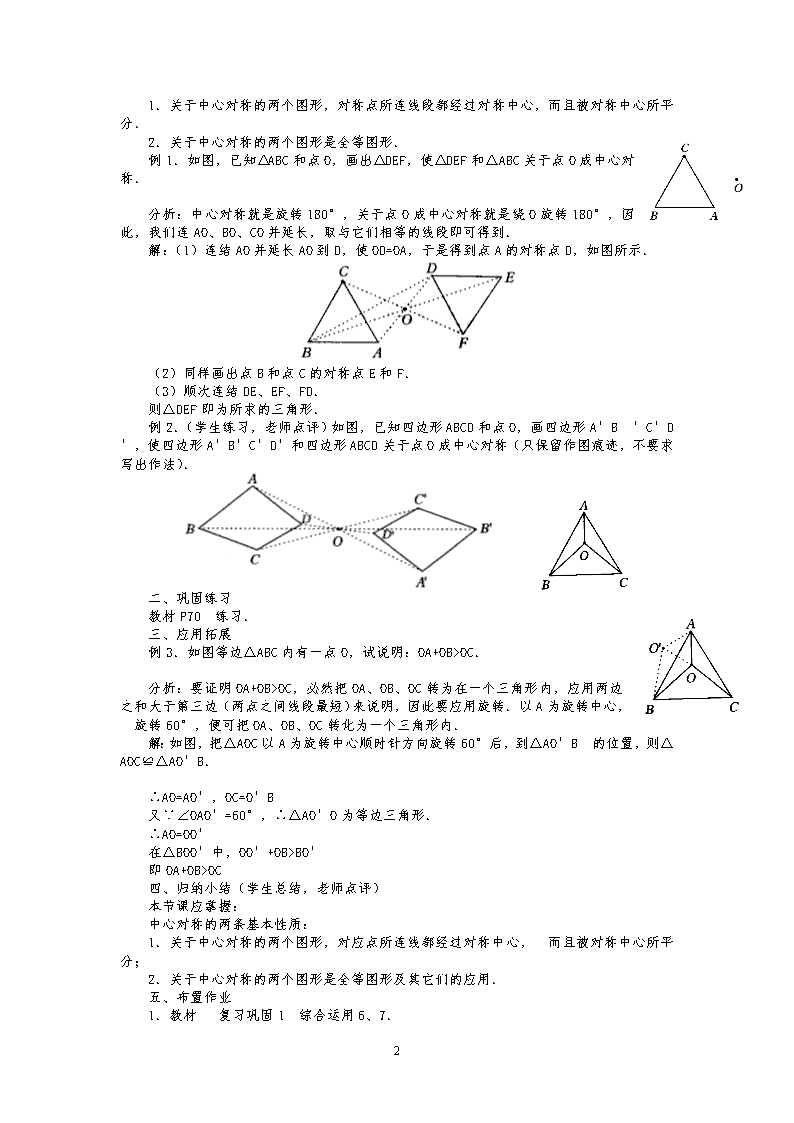
‎ 23.2 中心对称(2)‎ 第二课时 ‎ 教学内容 ‎ 1．关于中心对称的两个图形，对称点所连线段都经过对称中心，而且被对称中心所平分．‎ ‎ 2．关于中心对称的两个图形是全等图形．‎ ‎ 教学目标 ‎ 理解关于中心对称的两个图形，对称点所连线段都经过对称中心，而且被对称中心所平分；理解关于中心对称的两个图形是全等图形；掌握这两个性质的运用．‎ ‎ 复习中心对称的基本概念（中心对称、对称中心，关于中心的对称点），提出问题，让学生分组讨论解决问题，老师引导总结中心对称的基本性质．‎ ‎ 重难点、关键 ‎ 1．重点：中心对称的两条基本性质及其运用．‎ ‎ 2．难点与关键：让学生合作讨论，得出中心对称的两条基本性质．‎ ‎ 教学过程 ‎ 一、复习引入 ‎ （老师口问，学生口答）‎ ‎ 1．什么叫中心对称？什么叫对称中心？‎ ‎ 2．什么叫关于中心的对称点？‎ ‎ 3．请同学随便画一三角形，以三角形一顶点为对称中心，画出这个三角形关于这个对称中心的对称图形，并分组讨论能得到什么结论．‎ ‎ （每组推荐一人上台陈述，老师点评）‎ ‎ （老师）在黑板上画一个三角形ABC，分两种情况作两个图形 ‎ （1）作△ABC一顶点为对称中心的对称图形；‎ ‎ （2）作关于一定点O为对称中心的对称图形．‎ ‎ 第一步，画出△ABC．‎ 第二步，以△ABC的C点（或O点）为中心，旋转180°画出△A′B′和△A′B′C′，如图1和用2所示．‎ ‎ (1) (2)‎ ‎ 从图1中可以得出△ABC与△A′B′C是全等三角形； 分别连接对称点AA′、BB′、CC′，点O在这些线段上且O平分这些线段．‎ ‎ 下面，我们就以图2为例来证明这两个结论．‎ ‎ 证明：（1）在△ABC和△A′B′C′中，‎ ‎ OA=OA′，OB=OB′，∠AOB=∠A′OB′‎ ‎ ∴△AOB≌△A′OB′‎ ‎ ∴AB=A′B′‎ ‎ 同理可证：AC=A′C′，BC=B′C′‎ ‎ ∴△ABC≌△A′B′C′‎ ‎ （2）点A′是点A绕点O旋转180°后得到的，即线段OA绕点O旋转180°得到线段OA′，所以点O在线段AA′上，且OA=OA′，即点O是线段AA′的中点．‎ ‎ 同样地，点O也在线段BB′和CC′上，且OB=OB′，OC=OC′，即点O是BB′和CC′的中点．‎ ‎ 因此，我们就得到 3‎ ‎ 1．关于中心对称的两个图形，对称点所连线段都经过对称中心，而且被对称中心所平分．‎ ‎ 2．关于中心对称的两个图形是全等图形．‎ 例1．如图，已知△ABC和点O，画出△DEF，使△DEF和△ABC关于点O成中心对称．‎ ‎ 分析：中心对称就是旋转180°，关于点O成中心对称就是绕O旋转180°，因此，我们连AO、BO、CO并延长，取与它们相等的线段即可得到．‎ 解：（1）连结AO并延长AO到D，使OD=OA，于是得到点A的对称点D，如图所示．‎ ‎ （2）同样画出点B和点C的对称点E和F．‎ ‎ （3）顺次连结DE、EF、FD．‎ 则△DEF即为所求的三角形．‎ 例2．（学生练习，老师点评）如图，已知四边形ABCD和点O，画四边形A′B′C′D′，使四边形A′B′C′D′和四边形ABCD关于点O成中心对称（只保留作图痕迹，不要求写出作法）．‎ ‎ 二、巩固练习 ‎ 教材P70 练习．‎ ‎ 三、应用拓展 例3．如图等边△ABC内有一点O，试说明：OA+OB>OC．‎ ‎ 分析：要证明OA+OB>OC，必然把OA、OB、OC转为在一个三角形内，应用两边之和大于第三边（两点之间线段最短）来说明，因此要应用旋转．以A为旋转中心，旋转60°，便可把OA、OB、OC转化为一个三角形内．‎ 解：如图，把△AOC以A为旋转中心顺时针方向旋转60°后，到△AO′B的位置，则△AOC≌△AO′B．‎ ‎ ∴AO=AO′，OC=O′B ‎ 又∵∠OAO′=60°，∴△AO′O为等边三角形．‎ ‎ ∴AO=OO′‎ ‎ 在△BOO′中，OO′+OB>BO′‎ ‎ 即OA+OB>OC ‎ 四、归纳小结（学生总结，老师点评）‎ ‎ 本节课应掌握：‎ ‎ 中心对称的两条基本性质：‎ ‎ 1．关于中心对称的两个图形，对应点所连线都经过对称中心，而且被对称中心所平分；‎ ‎ 2．关于中心对称的两个图形是全等图形及其它们的应用．‎ ‎ 五、布置作业 ‎ 1．教材 复习巩固1 综合运用6、7．‎ ‎ ‎ 3‎ 3‎