- 2021-04-20 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2017-2018学年辽宁省抚顺市六校高二下学期期末考试数学(文)试题 Word版
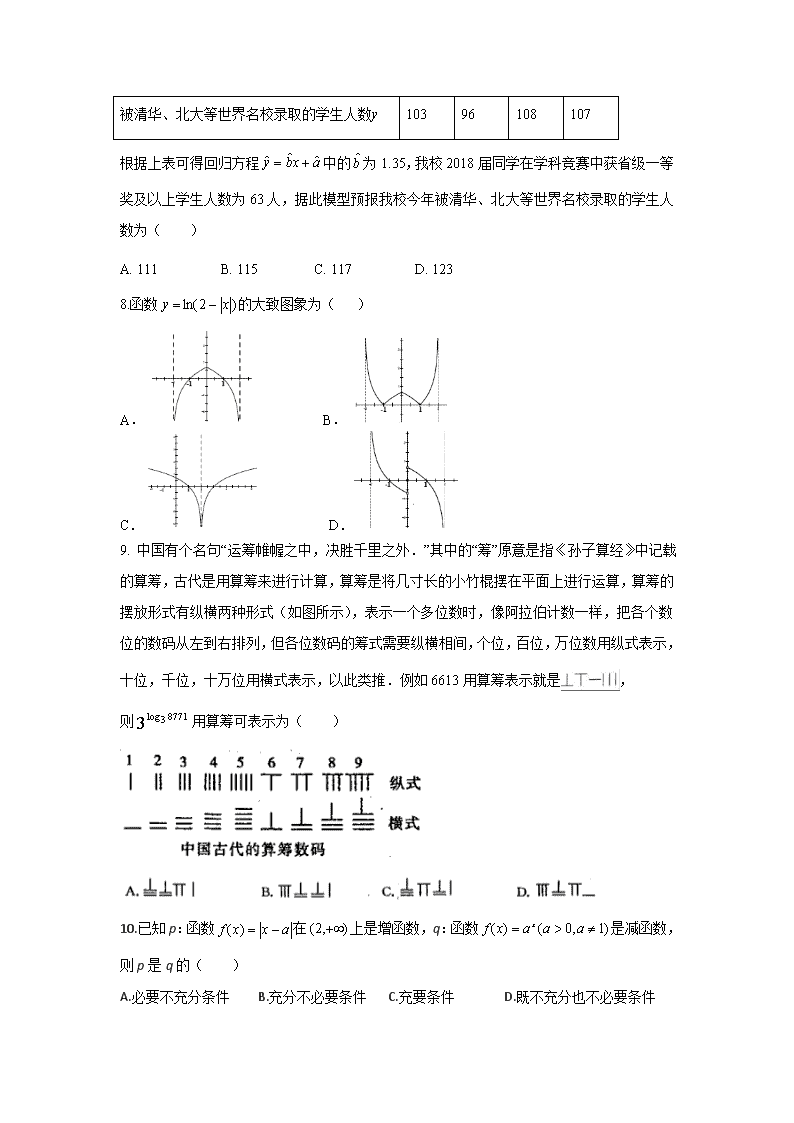
2017-2018学年辽宁省抚顺市六校高二下学期期末考试 数 学(文科) 命题单位:抚顺市十二中学 命题人:杨博 本试卷分第I卷(选择题)和第II卷(非选择题)两部分,时间为120分钟,满分150分 。 第I卷(60分) 一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。 1.设全集,集合,则( ) A. B. C. D. 2.若复数满足(为虚数单位),则=( ) A. B. C. D. 3.函数的单调增区间为( ) A. B. C. D. 4.命题“且”的否定形式是( ) A.且 B.或 C.且 D.或 5.若幂函数在(0,+∞)上为增函数,则实数m=( ) A. B. C. D. 或4 6.用反证法证明命题:“三角形的内角中至少有一个不大于”时,假设正确的是( ) A.假设三内角都不大于 B.假设三内角都大于 C.假设三内角至多有一个大于 D.假设三内角至多有两个大于 7.千年潮未落,风起再扬帆,为实现“两个一百年”奋斗目标、实现中华民族伟大复兴的中国梦奠定坚实基础,某中学积极响应国家号召,不断加大拔尖人才的培养力度,据不完全统计: 年份(届) 2014 2015 2016 2017 学科竞赛获省级一等奖及以上学生人数x 51 49 55 57 被清华、北大等世界名校录取的学生人数y 103 96 108 107 根据上表可得回归方程中的为1.35,我校2018届同学在学科竞赛中获省级一等奖及以上学生人数为63人,据此模型预报我校今年被清华、北大等世界名校录取的学生人数为( ) A. 111 B. 115 C. 117 D. 123 8.函数的大致图象为( ) A. B. C. D. 9. 中国有个名句“运筹帷幄之中,决胜千里之外.”其中的“筹”原意是指《孙子算经》中记载的算筹,古代是用算筹来进行计算,算筹是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放形式有纵横两种形式(如图所示),表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,个位,百位,万位数用纵式表示,十位,千位,十万位用横式表示,以此类推.例如6613用算筹表示就是, 则用算筹可表示为( ) 10.已知p:函数在上是增函数,q:函数是减函数,则p是q的( ) A.必要不充分条件 B.充分不必要条件 C.充要条件 D.既不充分也不必要条件 11.若函数的零点为,若,则的值满足( ) A. B. C. D.的符号不确定 12.已知函数任意,都有图象关于点(1,0)对称,,则( ) A. B. C. D. 第Ⅱ卷(90分) 二、填空题:本大题共4小题,每小题5分,共20分. 13.函数的定义域为_______________. 14. 设是定义在上的偶函数,且在上为增函数,则的解集为_________________. 15.甲乙丙三人代表班级参加校运会的跑步,跳远,铅球比赛,每人参加一项,每项都要有人参加,他们的身高各不同,现了解到已下情况:(1)甲不是最高的;(2)最高的是没报铅球;(3)最矮的参加了跳远;(4)乙不是最矮的,也没参加跑步.可以判断丙参加的比赛项目是 ________. 16.已知函数在上单调递增,则的取值范围是________. 三、解答题:本大题共5小题,每小题12分,共60分. 17.已知是复数,均为实数, (1)求复数; (2)若复数在复平面内对应的点在第一象限,求实数的取值范围. 18.已知命题p:关于的方程有实根;命题q:关于的函数在是增函数,若为真,为假,求a的取值范围. 19.已知为定义在上的奇函数,当时,函数解析式为. (1)求b的值,并求出在上的解析式; (2)若对任意的,总有,求实数a的取值范围. 20.某城市随机抽取一年(365天)内100天的空气质量指数API的监测数据,结果统计如下: API [0,100] (100,200] (200,300] >300 空气质量 优良 轻污染 中度污染 重度污染 天数 17 45 18 20 记某企业每天由空气污染造成的经济损失S(单位:元),空气质量指数API为.当时,企业没有造成经济损失;当对企业造成经济损失成直线模型(当时造成的经济损失为,当时,造成的经济损失);当时造成的经济损失为2000元; (1)试写出的表达式; (2)若本次抽取的样本数据有30天是在供暖季,其中有12天为重度污染,完成下面2×2列联表,并判断能否有99%的把握认为该市本年空气重度污染与供暖有关? 非重度污染 重度污染 合计 供暖季 非供暖季 合计 100 P(k2≥k0) 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001 k0 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828 21.函数对任意的都有,并且时,恒有. (1)求证:在R上是增函数; (2)若解不等式. 四、选做题:本大题共1小题,共10分,请选择22或23题做一道即可. 22.(本小题10分)选修4-4:坐标系与参数方程 在平面直角坐标系中,直线的参数方程为(其中为参数).现以坐标原点为极点,轴的非负半轴为极轴建立极坐标系,曲线的极坐标方程为. (1)写出直线的普通方程和曲线的直角坐标方程; (2)若点坐标为,直线交曲线于两点,求的值. 23. (本小题10分)已知函数. (1)当时,求关于x的不等式的解集; (2)若关于x的不等式有解,求a的取值范围. 2017-2018学年度下学期六校协作体高二期末考试试题 数学答案(文科) 1.A 2.C 3.D 4.D 5.A 6. B 7.C 8.A 9.C 10.A 11.B 12.B 13. 14. 15. 跑步 16. 17.(1)设复数,由题意,, 所以,即. 又,所以,即, 所以.-------------------------------------------------------(6分) (2)由(1)可知,因为 对应的点在复平面的第一象限,所以, 解得a的取值范围为.----------------------------------(12分) 18.命题p:关于x的方程有实根,则, 解得;-----------------------------------------(4分) 命题q:关于的函数在是增函数,所以, 解得.-----------------------------------------------------------(8分) 若为真,为假,则p与q必然一真一假, 所以.,或,解得,所以实数a的取值范围是.-----------------------(12分) 19.(1)因为函数为定义在上的奇函数, 当时,函数解析式为. 所以,解得, 即当时的解析式, 当时,,所以 又因为,所以-----------------------------------(6分) (2)由(1)得:当时,,令,则, 令,则易得出当时,y有最小值-2,即在上的最小值为-2,因为对任意的,总有,所以.----------------------------------(12分) 20. (1)---------------------------------------------(4分) (2)根据以上数据得到如下列联表: 则计算可得 所以有的把握认为该市本年空气重度污染与供暖有关.-----------------------------(12分) 21.(1)证明:设,且,则,所以, , 即,所以是R上的增函数.----------------------------------------------(6分) (2)因为,不妨设,所以,即,,所以. ,因为在R上为增函数,所以得到, 即.-------------------------------------------------------------------------------------(12分) 22(1)由消去参数,得直线的普通方程为 又由得, 由得曲线的直角坐标方程为-------------------------------(5分) (2)将其代入得, 则 所以.----------------------------------------------------------(10分) 23.(1)当时,不等式为. 若,则即; 若,则舍去; 若,则即; 综上,不等式的解集为-------------------------------------------------------(5分) (2)因为,得到的最小值为, 所以,得.--------------------------------------------------------------(10分)查看更多