- 2021-04-19 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
北师大版数学九年级 上册 第四章 4
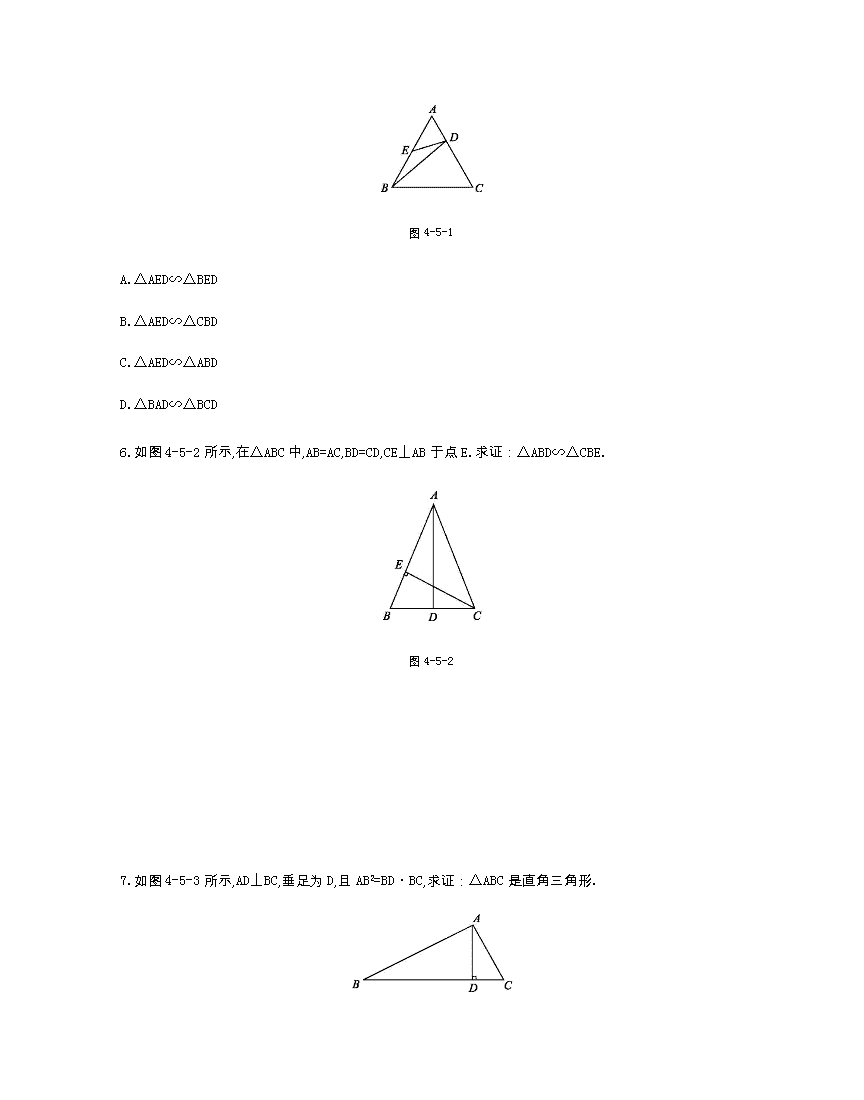
北师大版九年级 上册 第四章 图形的相似 4.5相似三角形判定定理的证明 同步练习 1. 分别相等的两个三角形相似. 2. 对应成比例且 相等的两个三角形相似. 3. 成比例的两个三角形相似. 4.下列语句正确的是( ) A.在△ABC和△A’B’C’中,∠B=∠B’=90°,∠A=30°,∠C’=60°,则△ABC和△A’B’C’不相似 B.在△ABC和△A’B’C’中,AB=5,BC=7,AC=8,A’C’=16,B’C’=14,A’B’=10,则△ABC∽△A’B’C’ C.两个全等三角形不一定相似 D.所有的菱形都相似 5.如图4-5-1所示,在正三角形ABC中,D、E分别在AC、AB上,且=,AE=BE,则有( ) 图4-5-1 A.△AED∽△BED B.△AED∽△CBD C.△AED∽△ABD D.△BAD∽△BCD 6.如图4-5-2所示,在△ABC中,AB=AC,BD=CD,CE⊥AB于点E.求证:△ABD∽△CBE. 图4-5-2 7.如图4-5-3所示,AD⊥BC,垂足为D,且AB2=BD·BC,求证:△ABC是直角三角形. 图4-5-3 8.如图4-5-4所示,△ABC是等边三角形,点D,E分别在CB,AC的延长线上,∠ADE=60°.求证:△ABD∽△DCE. 图4-5-4 9.如图4-5-5所示,AD,A’D’分别是△ABC和△A’B’C’的角平分线,且==,你认为△ABC和△A’B’C’相似吗?请说明理由. 图4-5-5 10.已知一个三角形三边长是6 cm,7.5 cm,9 cm,另一个三角形的三边长是8 cm,10 cm,12 cm,则这两个三角形 .(填“相似”或“不相似”) 11.如图4-5-6所示,平行四边形ABCD中,M是BC的中点,且AM=9,BD=12,AD=10,则该平行四边形的面积是 . 图4-5-6 12.如图4-5-7所示,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC. 图4-5-7 13.如图4-5-8所示,在直角梯形BACD中,AC⊥CD,AC=CD=4AB,E是AC的中点,求证:△ABE∽△CED. 图4-5-8 14.如图4-5-9所示,在△ABC中,∠BAC=90°,M是BC的中点,DM⊥BC交AC于点E,交BA的延长线于点D,求证:MA2=MD·ME. 图4-5-9 参考答案 1.两角 2.两边 夹角 3.三边 4.B 5.B 6.证明:在△ABC中,AB=AC,BD=CD, ∴AD⊥BC. ∵CE⊥AB, ∴∠ADB=∠CEB=90°. 又∵∠B=∠B, ∴△ABD∽△CBE. 7.证明:∵AB2=BD·BC, ∴=. 又∵∠B=∠B, ∴△ABC∽△DBA. ∵AD⊥BC, ∴∠BAC=∠BDA=90°. ∴△ABC是直角三角形. 8.证明:在等边三角形ABC中, ∠ABC=∠ACB=60°, ∴∠ABD=∠DCE=120°. 又∵∠ADB+∠DAB=∠ABC=60°, ∠ADB+∠EDC=60°, ∴∠DAB=∠EDC, ∴△ABD∽△DCE. 9.解:△ABC∽△A’B’C’.理由如下: ∵==, ∴△ABD∽△A’B’D’. ∴∠B=∠B’,∠BAD=∠B’A’D’. ∵∠BAC=2∠BAD, ∠B’A’C’=2∠B’A’D’, ∴∠BAC=∠B’A’C’. ∴△ABC∽△A’B’C’. 10.相似 11.72 12.证明:∵DE∥BC, ∴∠AED=∠C. 又∵EF∥AB, ∴∠A=∠FEC. ∴△ADE∽△EFC. 13.证明:在直角梯形BACD中,AC⊥CD,AB∥CD, ∴AC⊥AB, 即∠BAE=∠ECD=90°. ∵AC=CD=4AB, E是AC的中点, ∴=2,=2, ∴=, ∴△ABE∽△CED. 14.证明:∵DM⊥BC, ∴∠BMD=∠BAC=90°. 又∵∠B=∠B, ∴△BMD∽△BAC, ∴∠D=∠C. ∵M是BC的中点, ∴AM=MC=BC, ∴∠MAE=∠C,∴∠MAE=∠D. 又∵∠AME=∠DMA, ∴△EMA∽△AMD, ∴=, ∴MA2=MD·ME.查看更多