7年级数学教案第5讲：阶段复习与检测

7年级数学教案第5讲：阶段复习与检测

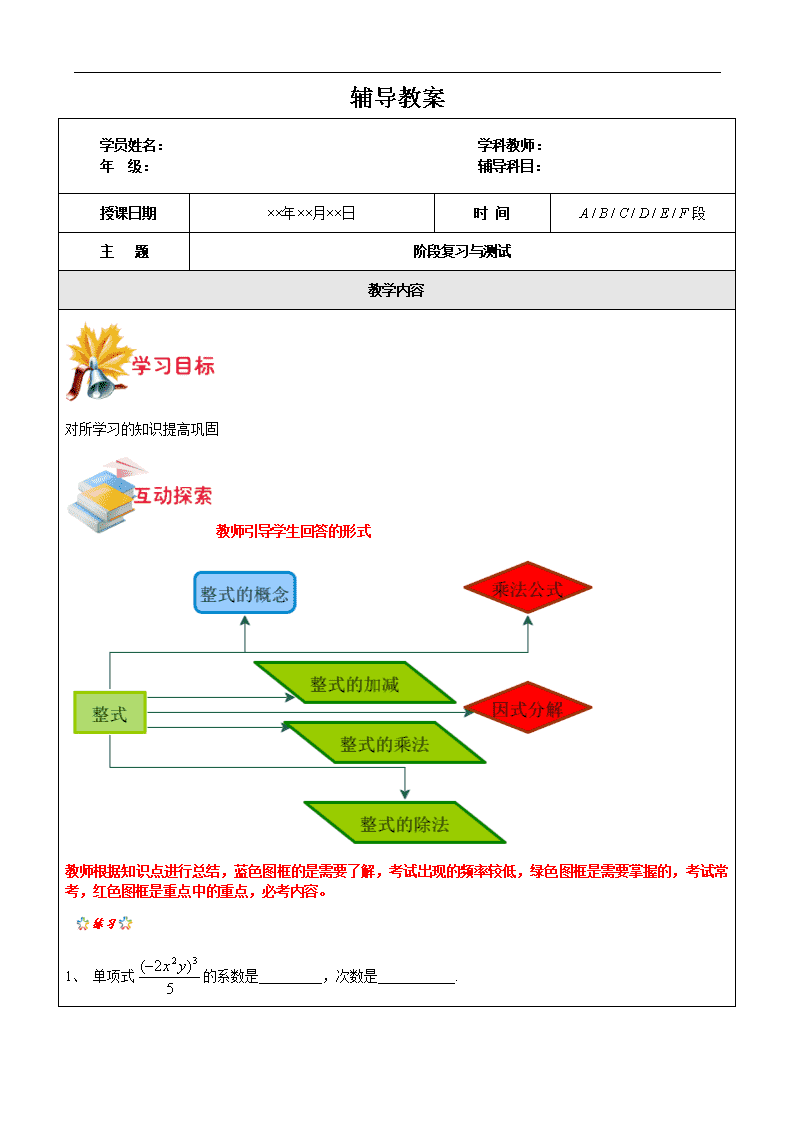
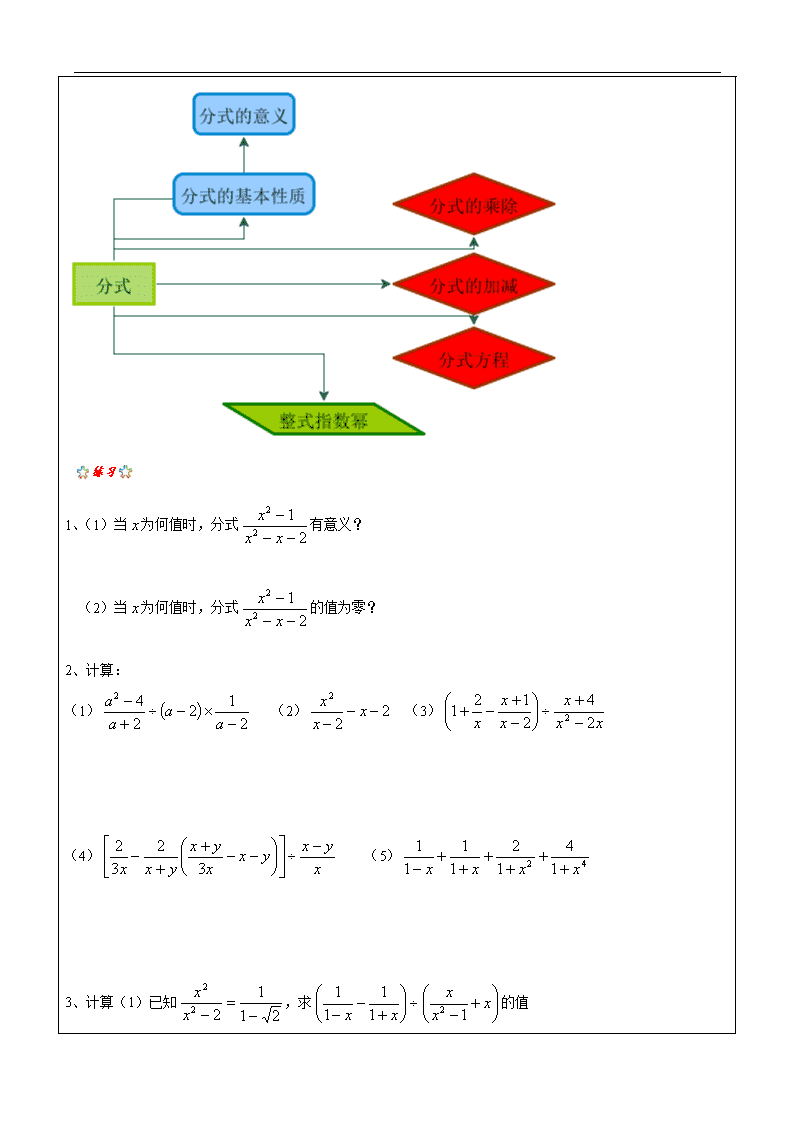
辅导教案 学员姓名： 学科教师：‎ 年 级： 辅导科目： ‎ 授课日期 ‎××年××月××日 ‎ 时 间 A / B / C / D / E / F段 主 题 阶段复习与测试 教学内容 对所学习的知识提高巩固 教师引导学生回答的形式 教师根据知识点进行总结，蓝色图框的是需要了解，考试出现的频率较低，绿色图框是需要掌握的，考试常考，红色图框是重点中的重点，必考内容。‎ 1、 单项式的系数是_________，次数是___________.‎ 1、 多项式中，三次项系数是_______，常数项是_________.‎ 2、 若则.‎ 3、 若，则.‎ 4、 ‎.‎ 5、 先化简，再求值 ‎（1），其中 ‎（2）已知 当时，求 的值 答案：‎ ‎1、 2、 3、 4、 ‎ ‎5、 6、（1） （2）‎ ‎1、（1）当为何值时，分式有意义？‎ ‎（2）当为何值时，分式的值为零？‎ ‎2、计算：‎ ‎（1） （2） （3）‎ ‎（4） （5）‎ ‎3、计算（1）已知，求的值 ‎（2）已知（≠0，≠0），求的值 ‎4、 进入防汛期后，某地对河堤进行了加固．该地驻军在河堤加固的工程中出色完成了任务．这是记者与驻军工程指挥官的一段对话:‎ 我们加固‎600米后,采用新的加固模式,这样每天加固长度是原来的2倍．‎ 你们是用9天完成‎4800米长的大坝加固任务的?‎ 通过这段对话,请你求出该地驻军原来每天加固的米数.‎ 答案：1、（1）≠2且≠－1；（2）＝1 ； ‎ ‎2、（1）；（2）；（3）（4）；（5）‎ ‎3、 （1）原式＝ ∵ ∴‎ ‎ ∴ ∴ ∴原式＝‎ ‎（2）原式＝ ∵ ∴‎ ‎ ∴或 当时，原式＝－3；当时，原式＝2‎ ‎4、解：设原来每天加固x米，根据题意，得 ‎ ‎． 去分母，得 1200+4200=18x（或18x=5400） 解得 ． 检验：当时，（或分母不等于0）．‎ ‎∴是原方程的解． ‎ ‎1．下列图案中，可以由一个“基本图案”连续旋转45°得到的是（　　）‎ ‎　　　 A．　　　 　B．　　 　C．　　　 　D．‎ ‎2. 下列说法正确的是（　　）‎ A．平移不改变图形的形状和大小，而旋转则改变图形的形状和大小 B．平移和旋转的共同点是改变图形的位置 C．图形可以向某方向平移一定距离，也可以向某方向旋转一定距离 D．由平移得到的图形也一定可由旋转得到 ‎3. 请画一个圆，画出圆的直径AB，分析直径AB两侧的两个半圆可以怎样相互得到？‎ ‎4. 在图中，将大写字母A绕它上侧的顶点按逆时针方向旋转90°，作出旋转后的图案．‎ 答案：1、 B； 2、 B； 3、略 ‎4、将其中的关键点绕上顶点逆时针旋转90°后，连接各关键点成“A”即可．图略 由学生独立完成，然后交换批改，进行讲解评比 一、选择题（每题3分，满分12分）‎ ‎1．下列运算正确的是 （ ）‎ ‎（A）； （B）； （C）； （D）． ‎ ‎2．下列各式是5次单项式的是 （ ）‎ ‎（A）； （B）； （C）； （D）．‎ ‎3．化简的结果是 （ ）‎ ‎（A）； （B）； （C）； （D）．‎ ‎4．下列图形中，可能是轴对称图形的为 （ ）‎ ‎（A） （B） （C） （D）‎ ‎ ‎ 二、填空题（每小题4分，满分44分）‎ ‎5．“比m的3倍少5的数”用代数式表示为 ． ‎ ‎6．计算： ＝ ．‎ ‎7．计算：＝ ．‎ ‎8．分解因式：＝ ．‎ ‎9．在多项式的各项中，的同类项是 ．‎ ‎10．如果分式有意义，那么的取值范围为 ． ‎ ‎11．计算：_____________.‎ ‎12．计算： = ． ‎ ‎13．如果，那么n= ．‎ ‎14．在圆、正方形、线段、角中，是轴对称图形但不是中心对称图形的图形是_________.‎ ‎15．如图，△ABC沿AB平移后得到△DEF，其中点A落在线段AB上的 点D，已知AB=‎6cm, BD=‎2cm，那么△ABC平移的距离是 cm． ‎ 三、简答题（16---18每题6分，19题8分，20、21题每题9分）‎ ‎16．计算：（； ‎ ‎17．分解因式：． ‎ ‎18．解方程：．‎ ‎19. 某服装厂接到加工400套校服的任务，在加工完160套后，采用了新技术，这样每天加工服装的套数是原来的2倍，结果共用了14天完成任务．问原来每天加工服装多少套？‎ ‎20. 已知△ABC中，点B、C关于直线MN对称，‎ （1） 画出直线MN；‎ （2） 画出△ABC关于直线MN 的对称图形． ‎ ‎21. 先化简，再求值：，其中．‎ 答案：1．D； 2．B； 3．A； 4． D； ‎ ‎5．‎3m-5； 6．-27； 7．； 8． m（m+4）； 9．；10．；11．； 12．； 13．-5； 14．角 ； 15．4； ‎ ‎16. 原式=‎ ‎=‎ ‎=‎ ‎17. 原式=2（n-m）[] ‎ ‎=2（n-m）‎ ‎=2（n-m）‎ ‎18. 解：方程两边同乘以（x +3）（x -3）， ‎ 解这个整式方程得：， ‎ 经检验：是原方程的解，所以原方程的解是．‎ ‎19. 解：设原来每天加工服装套， ‎ ‎ 根据题意得： ． ‎ 解得：． ‎ 经检验是原方程的解，且符合题意． ‎ 答：原来每天加工服装20套．‎ ‎20. ‎ ‎21. 解：方法一：原式=‎ ‎ =‎ ‎ =‎ 当时，原式=． ‎ 方法二：原式=‎ ‎=‎ ‎=‎ ‎ =‎ 当时，原式=．‎ 本节课是复习巩固课，通过学生对知识点存在的问题进行总结 ‎1、已知则（ ）‎ ‎ A、 B、‎50 C、500 D、不知道 ‎2、则（ ）‎ ‎ A、 B、‎8 C、0 D、‎ ‎3、一个正方形的边长若增加3cm，它的面积就增加39cm，这个正方形的边长原来是（ ）‎ ‎ A、8cm B、6cm C、5cm D、10cm ‎4、若方程有增根，则的值可能是______________．‎ ‎5、化简：‎ ‎6、解方程：‎ ‎1. 能否将两个边长为1的正方形剪拼成一个大正方形？怎样剪拼？它的面积是多少？边长如何用代数符号表示？‎ ‎2. ‎ 答案：1、B；2、B；3、C； 4、6；5、；6、无解；7、90千米/时，100千米/时；‎ ‎8、（1）如图 ‎（2）由旋转图形的性质可知 CD=DG=a，AD=DE=b，∠DCF=∠DAE=90°‎ ‎∴∠ADC+∠EDG=180°‎ 即A、D、G三点共线 ‎= ‎ ‎（3）因为 ‎ =‎ ‎ =‎ ‎ =‎ ‎ 所以= ，‎ ‎ 得 ‎ ‎ 所以CH=CD-DH=‎