2017-2018学年山东省潍坊市高二上学期期中考试数学（文）试题（解析版）

2017-2018学年山东省潍坊市高二上学期期中考试数学（文）试题（解析版）

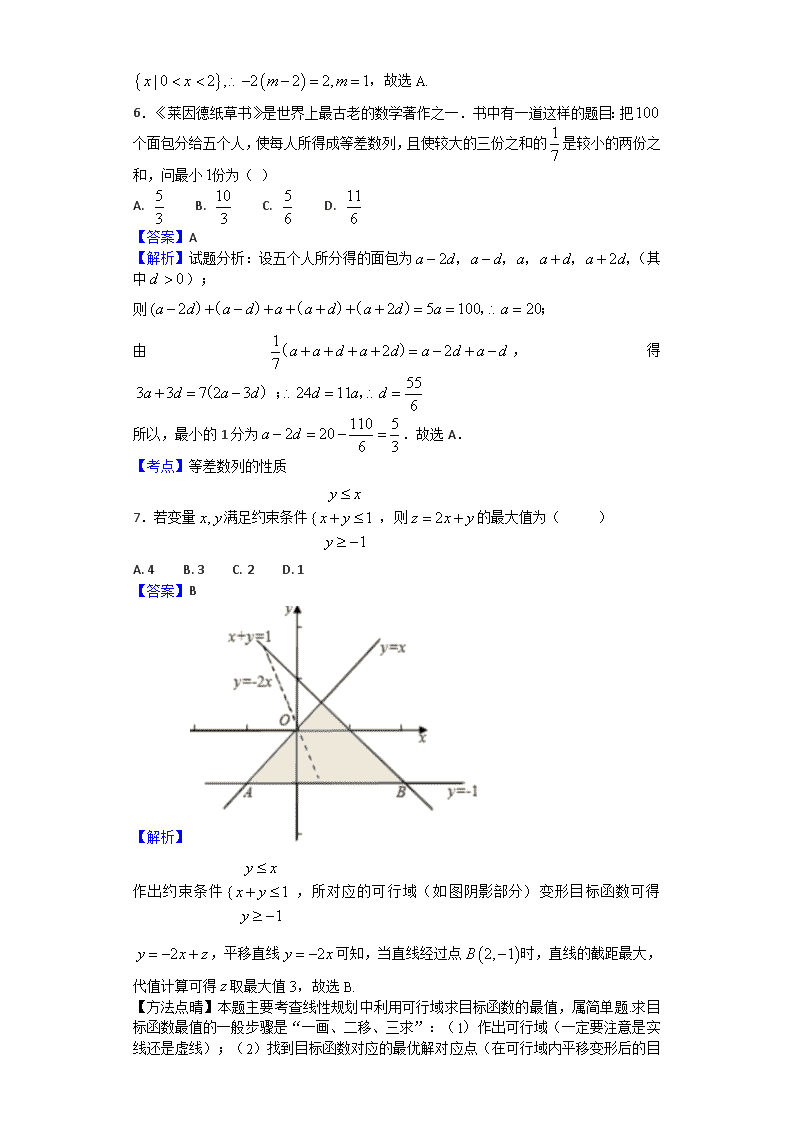
‎2017-2018学年山东省潍坊市高二上学期期中考试数学（文）试题 一、选择题 ‎1．已知，，那么一定正确的是（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】试题分析：由同向不等式的加法性质可知由，可得 ‎【考点】不等式性质 ‎2．设是等差数列的前项和，若，则（ ）‎ A. 5 B. 7 C. 9 D. 11‎ ‎【答案】A ‎【解析】， ，选A.‎ ‎3．若的三个内角满足，则是 A.锐角三角形 B.直角三角形 C.钝角三角形 D.可能是锐角三角形，也可能是钝角三角形.‎ ‎【答案】C ‎【解析】解;因为的三个内角满足，利用余弦定理求解最大角，然后可以判定最大角的余弦值为负数，说明了该三角形为钝角三角形，选C ‎4．设是等比数列，下列说法一定正确的是（ ）‎ A. 成等比数列 B. 成等比数列 C. 成等比数列 D. 成等比数列 ‎【答案】D ‎【解析】 ‎ 项中，故项说法错误； 项中，故项说法错误； 项中，故项说法错误；故项中，故项说法正确，故选D.‎ ‎5．若关于的不等式的解集为，则实数的值是（ ）‎ A. 1 B. 2 C. 3 D. 4‎ ‎【答案】A ‎【解析】解集为 ‎，故选A.‎ ‎6．《莱因德纸草书》是世界上最古老的数学著作之一．书中有一道这样的题目：把个面包分给五个人，使每人所得成等差数列，且使较大的三份之和的是较小的两份之和，问最小份为（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】试题分析：设五个人所分得的面包为（其中）；‎ 则 由，得 所以，最小的1分为．故选A．‎ ‎【考点】等差数列的性质 ‎7．若变量满足约束条件，则的最大值为（ ）‎ A. 4 B. 3 C. 2 D. 1‎ ‎【答案】B ‎【解析】‎ 作出约束条件，所对应的可行域（如图阴影部分）变形目标函数可得，平移直线可知，当直线经过点时，直线的截距最大，代值计算可得取最大值，故选B.‎ ‎【方法点晴】本题主要考查线性规划中利用可行域求目标函数的最值，属简单题.求目标函数最值的一般步骤是“一画、二移、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2‎ ‎）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值.‎ ‎8．设是等差数列，下列结论中正确的是（ ）‎ A. 若，则 B. 若，则 C. 若，则 D. 若，则 ‎【答案】B ‎【解析】选项中， ，分别取 即可得错误；假设，则，公差， ，即正确；C选项中， ，分别取 即可得C错误； 项中无法判断公差的正负，故无法判断正负，即错误，故选B.‎ ‎9．在等腰中，内角所对应的边分别为， ， ，则此三角形的外接圆半径和内切圆半径分别是（ ）‎ A. 4和2 B. 4和 C. 2和 D. 2和 ‎【答案】C ‎【解析】等腰中， ， ，可得 由正弦定理可得， ，由面积相等 可得，故选C.‎ ‎10．若是函数的两个不同的零点，且这三个数依次成等比数列， 这三个数依次成等差数列，则（ ）‎ A. 4 B. 5 C. 9 D. 20‎ ‎【答案】D ‎【解析】因为是函数的两个不同的零点，所以，可得，又这三个数依次成等比数列， 这三个数依次成等差数列，，可得解得； ‎ ‎，则，故选D.‎ ‎11．设， ，若， ， ，则下列关系式中正确的是（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】由题意可得：若， ， ， ，故选B.‎ ‎12．已知两个等差数列和的前项和分别为， ，且，则使得为整数的正整数的个数是（ ）‎ A. 2 B. 3 C. 4 D. 5‎ ‎【答案】C ‎【解析】数列和均为等差数列，且前项和和，满足，可得，则 ，验证知，当时， 为整数，即使得为整数的正整数的个数是 ，故选C.‎ ‎【方法点睛】本题主要考查等差数列的求和公式及等差数列的性质，属于难题. 等差数列的常用性质有：(1)通项公式的推广： (2)若 为等差数列，且 ；(3)若是等差数列，公差为 ，则是公差 的等差数列；(4)数列也是等差数列本题的解答运用了性质（2）.‎ 二、填空题 ‎13．函数的最小值为__________．‎ ‎【答案】5‎ ‎【解析】， ，当且仅当时取等号，故答案为.‎ ‎【易错点晴】本题主要考查利用基本不等式求最值，属于难题.利用基本不等式求最值时，一定要正确理解和掌握“一正，二定，三相等”的内涵：一正是，首先要判断参数是否为正；二定是，其次要看和或积是否为定值（和定积最大，积定和最小）；三相等是，最后一定要验证等号能否成立（主要注意两点，一是相等时参数否在定义域内，二是多次用或时等号能否同时成立）.‎ ‎14．已知数列是递减等比数列，且， ，则数列的通项公式__________．‎ ‎【答案】‎ ‎【解析】因为， ，所以, ,又因为数列是递减等比数列，所以 ，数列的通项公式 ，故答案为.‎ ‎15．已知中，满足， 的三角形有两解，则边长的取值范围为__________．‎ ‎【答案】‎ ‎【解析】在中， ，由正弦定理可得， ，若此三角形有两解，必须满足的条件为： ，即，故答案为.‎ ‎16．寒假期间，某校家长委员会准备租赁两种型号的客车安排900名学生到重点高校进行研究旅行， 两种客车的载客量分别为36人和60人，租金分别为1200元/辆和1800元/辆，家长委员会为节约成本，要求租车总数不超过21辆，且型车不多于型车7辆，则租金最少为__________元．‎ ‎【答案】27600‎ ‎【解析】‎ 设分别租用两种型号的客车辆， 辆，所用的总租金为元，则，其中满足不等式组，即，由，得，作出不等式组对应的平面区域平移，由图象知当直线经过点时，直线的截距最小，此时最小，由得，即当时，此时的总租金元，达到最小值，故答案为.‎ 三、解答题 ‎17．解下列关于的不等式：‎ ‎（1）；（2）.‎ ‎【答案】(1) ；（2）详见解析.‎ ‎【解析】试题分析：（1）化为，等价 不等式求解即可；（2）分三种情况讨论，分别求解一元二次不等式即可.‎ 试题解析：（I）将原不等式化为， ‎ 即 ‎ 所以原不等式的解集 . ‎ ‎（II）当时，不等式的解集为{0}； ‎ 当时，原不等式等价于，‎ 因此 当时， ， ‎ 当时， ， ‎ 综上所述，当时，不等式的解集为{0}，当时，不等式的解集为， ,当时，不等式的解集 ‎ ‎18．已知的内角所对应的边分别为，且满足.‎ ‎（1）判断的形状；‎ ‎（2）若， ， 为角的平分线，求的面积.‎ ‎【答案】(1) 直角三角形;(2) ‎ ‎【解析】试题分析：（1）由两角差的余弦函数公式，两角和的余弦函数公式，三角形内角和定理，诱导公式化简可求，即可判定三角形的形状；（2）由已知利用勾股定理可求，利用三角形内角和定理可求，由正弦定理可求的值，再利用三角形面积公式得结果.‎ 试题解析：（I）由，得 ‎, ‎ ‎,. ‎ ‎, 故为直角三角形. ‎ ‎(II)由（I）知，又，‎ ‎ ， , ‎ 由正弦定理得,‎ ‎， ‎ ‎19．设是等差数列的前项和，已知， ， .‎ ‎（1）求；‎ ‎（2）若数列，求数列的前项和.‎ ‎【答案】(1)18;(2) ‎ ‎【解析】试题分析：（1）根据等差数列满足， ，列出关于首项、公差的方程组，解方程组可得与的值，根据等差数列的求和公式可得递的值；（2）由（1）知，从而可得，利用裂项相消法求解即可.‎ 试题解析：（I）设数列的公差为，则 即 ， ‎ 解得， ‎ 所以. ‎ ‎（也可利用等差数列的性质解答）‎ ‎ (II)由（I）知， ‎ ‎， ‎ ‎ ‎ ‎ ‎ ‎【方法点晴】本题主要考查等差数列的通项与求和公式，以及裂项相消法求数列的和，属于中档题. 裂项相消法是最难把握的求和方法之一，其原因是有时很难找到裂项的方向，突破这一难点的方法是根据式子的结构特点，常见的裂项技巧：(1) ；（2） ； （3）；（4） ；此外，需注意裂项之后相消的过程中容易出现丢项或多项的问题，导致计算结果错误.‎ ‎20．已知的内角所对应的边分别为，且.‎ ‎（1）求；‎ ‎（2）若，求的取值范围.‎ ‎【答案】(1) ;(2) ‎ ‎【解析】试题分析：(1) 由利用正弦定理得，再利用两角差和的正弦公式化简可得所以；（2）由余弦定理结合条件，可得，利用二次函数的性质可得结果.‎ 试题解析：(I）‎ ‎,‎ 即,‎ ‎, 在中，‎ 可得所以. ‎ ‎(II）∵，即， ， ‎ ‎∴由余弦定理得： ，即 ‎∵，∴则 ‎21．潍坊文化艺术中心的观光塔是潍坊市的标志性建筑，某班同学准备测量观光塔的高度（单位：米），如图所示，垂直放置的标杆的高度米，已知， .‎ ‎（1）该班同学测得一组数据： ，请据此算出的值；‎ ‎（2）该班同学分析若干测得的数据后，发现适当调整标杆到观光塔的距离（单位：米），使与的差较大，可以提高测量精确度，若观光塔高度为136米，问为多大时， 的值最大？‎ ‎【答案】(1) 135m;(2) .‎ ‎【解析】试题分析：(1)根据三角函数的定义及直角三角形的性质可得， ， ，利用，化简即可得结果；（2）由得，利用两角差的正切公式以及基本不等式可的值最大.‎ 试题解析：（I）由， ， , ‎ 及，‎ 得， ‎ 解得, ‎ 因此算出观光塔的高度是135m. ‎ ‎(II）由题设知，得，‎ 由得， ‎ 所以.‎ 当且仅当，即时，‎ 上式取等号，所以当时最大. ‎ ‎22．已知数列的前项和为， .‎ ‎（1）求数列的通项公式；‎ ‎（2）令，设数列的前项和为，求；‎ ‎（3）令，若对恒成立，求实数的取值范围.‎ ‎【答案】(1) ; (2) ;(3) ‎ ‎【解析】试题分析：(1) 当时，利用公式；，可得，验证当时是否适合即可；（2）由（1）可得，利用错位相减法求和即可（3）讨论当为奇数时，当为偶数时两种情况，分别利用等差数列求和公式求和，然后利用放缩法可证明结论.‎ 试题解析：(I)当时， ‎ 当时， ，适合上式，‎ ‎ （）. ‎ ‎(II) ，则， ‎ ‚， ‎ -‚得 ‎， ‎ ‎. ‎ ‎ . ‎ ‎(III) , ‎ 当为奇数时， ， ‎ ‎ ‎ ‎ ‎ 当为偶数时， ，‎ ‎ ‎ ‎ ‎ 综上所述， ‎ ‎ 【 方法点睛】本题主要考查等差数列的通项与求和公式以及错位相减法求数列的的前 项和，属于中档题.一般地，如果数列是等差数列， 是等比数列，求数列的前项和时，可采用“错位相减法”求和，一般是和式两边同乘以等比数列的公比，然后作差求解, 在写出“”与“” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“”的表达式. ‎