- 2021-04-19 发布 |
- 37.5 KB |
- 65页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学试题分类汇编32 解直角三角形
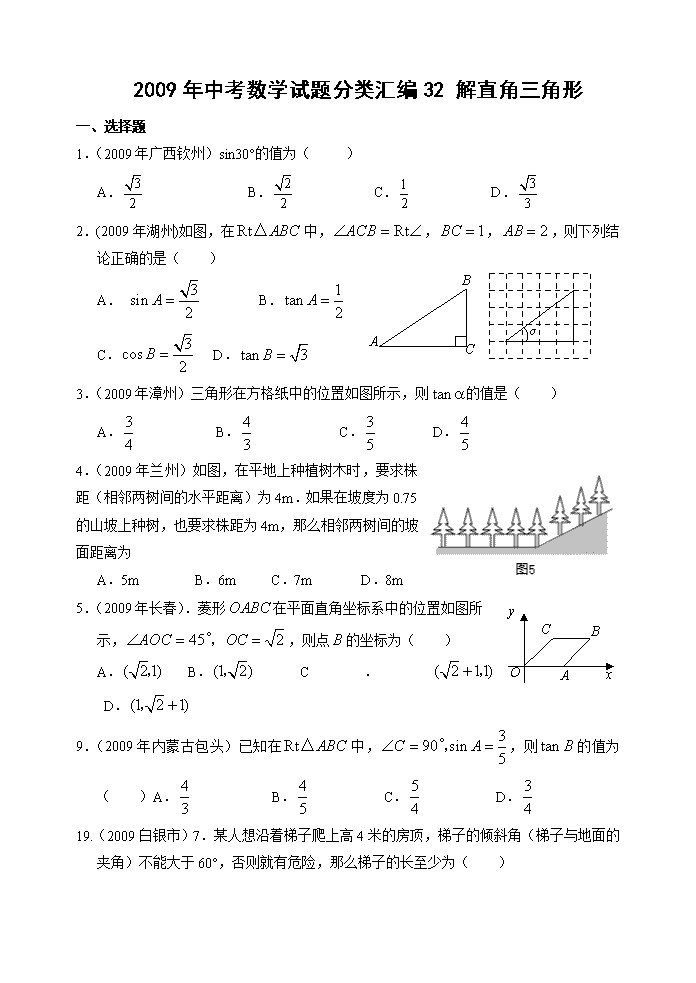
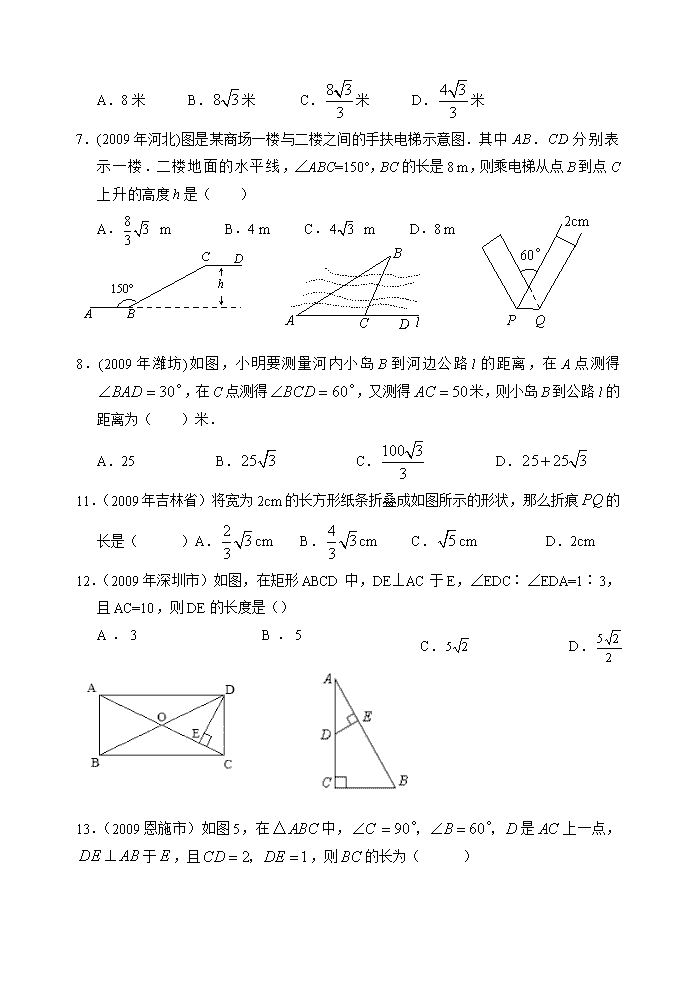
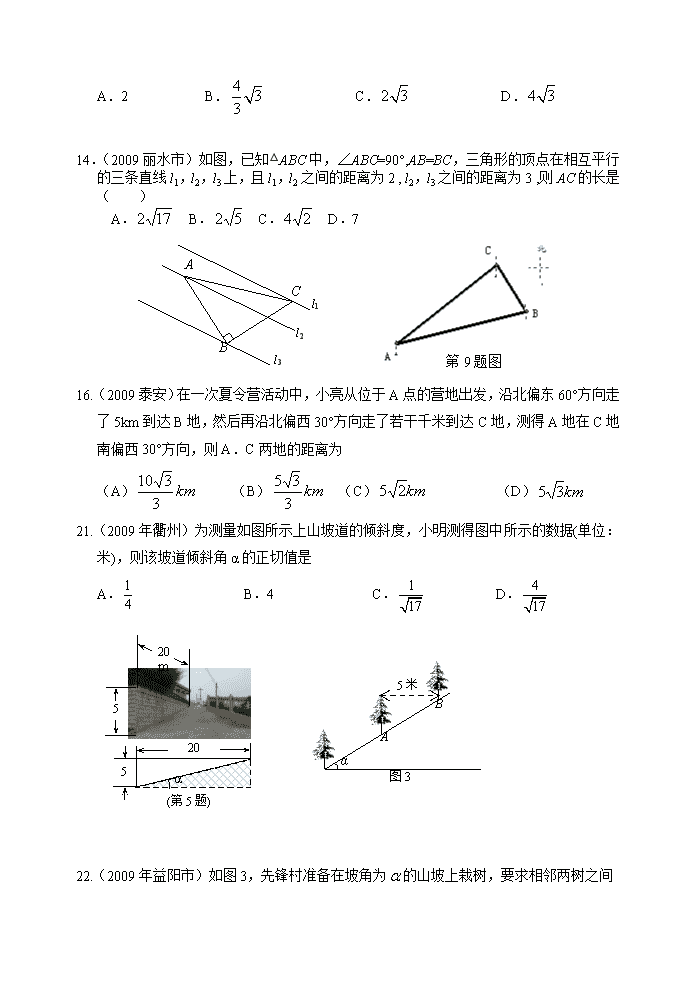
2009年中考数学试题分类汇编32 解直角三角形 一、选择题 1.(2009年广西钦州)sin30°的值为( ) A. B. C. D. 2.(2009年湖州)如图,在中,,,,则下列结论正确的是( )B C A α A. B. C. D. 3.(2009年漳州)三角形在方格纸中的位置如图所示,则的值是( ) A. B. C. D. 4.(2009年兰州)如图,在平地上种植树木时,要求株距(相邻两树间的水平距离)为4m.如果在坡度为0.75的山坡上种树,也要求株距为4m,那么相邻两树间的坡面距离为 A.5m B.6m C.7m D.8m 5.(2009年长春).菱形在平面直角坐标系中的位置如图所示x y O C B A ,,则点的坐标为( ) A. B. C. D. 9.(2009年内蒙古包头)已知在中,,则的值为( )A. B. C. D. 19.(2009白银市)7.某人想沿着梯子爬上高4米的房顶,梯子的倾斜角(梯子与地面的夹角)不能大于60°,否则就有危险,那么梯子的长至少为( ) A.8米 B.米 C.米 D.米 7.(2009年河北)图是某商场一楼与二楼之间的手扶电梯示意图.其中AB.CD分别表示一楼.二楼地面的水平线,∠ABC=150°,BC的长是8 m,则乘电梯从点B到点C上升的高度h是( ) A B C D 150° h A. m B.4 m B C A D l C. m D.8 m60° P Q 2cm 8.(2009年潍坊)如图,小明要测量河内小岛B到河边公路l的距离,在A点测得,在C点测得,又测得米,则小岛B到公路l的距离为( )米. A.25 B. C. D. 11.(2009年吉林省)将宽为2cm的长方形纸条折叠成如图所示的形状,那么折痕的长是( )A.cm B.cm C.cm D.2cm 12.(2009年深圳市)如图,在矩形ABCD中,DE⊥AC于E,∠EDC∶∠EDA=1∶3,且AC=10,则DE的长度是() A.3 B.5 C. D. 13.(2009恩施市)如图5,在中,是上一点,于,且,则的长为( ) A.2 B. C. D. 14.(2009丽水市)如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2 , l2,l3之间的距离为3 ,则AC的长是( ) A. B. C. D.7 第9题图 l1 l2 l3 A C B 16.(2009泰安)在一次夏令营活动中,小亮从位于A点的营地出发,沿北偏东60°方向走了5km到达B地,然后再沿北偏西30°方向走了若干千米到达C地,测得A地在C地南偏西30°方向,则A.C两地的距离为 (A) (B) (C) (D) 21.(2009年衢州)为测量如图所示上山坡道的倾斜度,小明测得图中所示的数据(单位:米),则该坡道倾斜角α的正切值是 A. B.4 C.5 m 20 m (第5题) α 5 m 20 m D. α 5米 A B 图3 22.(2009年益阳市)如图3,先锋村准备在坡角为 的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为 A. B. C. D. 18.(2009年天津市)2sin的值等于( ) A.1 B. C. D.2 17. (2009年鄂州)如图,在梯形ABCD中,AD//BC,AC⊥AB,AD=CD,cos∠DCA= ,BC=10,则AB的值是( ) A.3 B.6 C.8 D.9 23.(2009年衡阳市) 如图,菱形ABCD的周长为20cm,A B C D E DE⊥AB,垂足为E,,则下列结论中正确的个数为( ) ①DE=3cm; ②EB=1cm; ③. A.3个 B.2个 C.1个 D.0个 25.(2009年甘肃定西)某人想沿着梯子爬上高4米的房顶,梯子的倾斜角(梯子与地面的夹角)不能大于60°,否则就有危险,那么梯子的长至少为( ) A.8米 B.米 C.米 D.米 29.(2009青海)一根电线杆的接线柱部分AB在阳光下的投影CD的长为1米,太阳光线与地面的夹角,则AB的长为( ) A.米 B.米 C.米 D.米 二、填空题: 1.(2009年济南)如图,是放置在正方形网格中的一个角,则的值是 . 2.(2009年济南)九年级三班小亮同学学习了“测量物体高度”一节课后,他为了测得右图所放风筝的高度,进行了如下操作: (1)在放风筝的点处安置测倾器,测得风筝的仰角; (2)根据手中剩余线的长度出风筝线的长度为70米; (3)量出测倾器的高度米. 根据测量数据,计算出风筝的高度约为 米.(精确到0.1米,) A D B E C 60° (第17题图) 3. (2009仙桃)如图所示,小华同学在距离某建筑物6米的点A处测得广告牌B点.C点的仰角分别为52°和35°,则广告牌的高度BC为_____________米(精确到0.1米).(sin35°≈0.57,cos35°≈0.82,tan35°≈0.70;sin52°≈0.79,cos52°≈0.62,tan52°≈1.28) 4.(2009年安徽)长为4m的梯子搭在墙上与地面成45°角,作业时调整为60°角(如图所示),则梯子的顶端沿墙面升高了 m. 第13题图 5.(2009年桂林市.百色市)如图,在一次数学课外活动中,测得电线杆底部B与钢缆固定 点C的距离为4米,钢缆与地面的夹角为60º,则这条钢缆在电 线杆上的固定点A到地面的距离AB是 米.(结果保留根号). 第15题图 A B C 6.(2009湖北省荆门市)=______. 解析:本题考查特殊角的三角函数值.零指数幂.负整数指数幂的有关运算, =,故填. 7.(2009年齐齐哈尔市)用直角边分别为3和4的两个直角三角形拼成凸四边形,所得的四边形的周长是____________. 【关键词】直角三角形性质 【答案】14或16或18 8.(2009年宁波市)如图,在坡屋顶的设计图中,,屋顶的宽度为10米,坡角为35°,则坡屋顶高度为 米.(结果精确到0.1米) A B C h l 9.(2009桂林百色)15.如图,在一次数学课外活动中,测得电线杆底部B与钢缆固定点C的距离为4米,钢缆与地面的夹角为60º,则这条钢缆在电线杆上的固定点A到地面的距离AB是 米.(结果保留根号). 第15题图 A B C 10.(2009丽水市)将一副三角板按如图1位置摆放,使得两块三角板的直角边AC和MD重合. 已知AB=AC=8 cm,将△MED绕点A(M)逆时针旋转60°后(图2),两个三角形重11(阴影)部分的面积约是 ▲ cm2 (结果 精确到0.1,) . 11.(09湖南怀化)如图8,小明从地沿北偏东方向走到地,再从地向正南方向走到地,此时小明离地 . 12.2009年鄂州)小明同学在东西方向的沿江大道A处,测得江中灯塔P在北偏东60°方向上,在A处正东400米的B处,测得江中灯塔P在北偏东30°方向上,则灯塔P到沿江大道的距离为____________米. 【关键词】方位角 【答案】 13.(2009年孝感)如图,角的顶点为O,它的一边在x轴的正半轴上,另一边OA上有一点P(3,4),则 ▲ . 14.(2009泰安)如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CM将△CMA折叠,使点A落在点D处,若CD恰好与MB垂直,则tanA的值为 . 15.(2009年南宁市)17.如图,一艘海轮位于灯塔的东北方向,距离灯塔海里的处,它沿正南方向航行一段时间后,到达位于灯塔的南偏东方向上的处,则海轮行驶的路程为 _____________海里(结果保留根号). 16.(2009白银市)17.如图7,在△ABC中,,cosB.如果⊙O的半径为cm,且经过点B.C,那么线段AO= cm. 17.(2009年衡阳市)某人沿着有一定坡度的坡面前进了10米,此时他与水平地面的垂直距离为米,则这个破面的坡度为_________. 18..(2009年广西梧州)在△ABC中,∠C=90°, BC=6 cm,, 则AB的长是 ★ cm. 19.(2009年包头)如图,在中,,与相切于点,且交于两点,则图中阴影部分的面积是 (保留). A N C D B M 20.(2009年包头)如图,已知与是两个全等的直角三角形,量得它们的斜边长为10cm,较小锐角为30°,将这两个三角形摆成如图(1)所示的形状,使点在同一条直线上,且点与点重合,将图(1)中的绕点顺时针方向旋转到图(2)的位置,点在边上,交于点,则线段的长为 cm(保留根号).A E C (F) D B 图(1) E A G B C (F) D 图(2) 21. (2009宁夏)10.在中,,则的值是 . 22.(2009年山东青岛市)如图,长方体的底面边长分别为1cm 和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要 cm;如果从点A开始经过4个侧面缠绕圈到达点B,那么所用细线最短需要 cm. B A 6cm 3cm 1cm 第4题图 【关键词】直角三角形的有关计算.勾股定理 【答案】10,(或) 23.(2009年衡阳市)某人沿着有一定坡度的坡面前进了10米 ,此时他与水平地面的垂直距离为米,则这个破面的坡度为_________. 24.(2009年益阳市)如图7,将以A为直角顶点的等腰直角三角形ABC沿直线BC平移得到△,使点与C重合,连结,则的值为 . A C(B′) B A′ 图7 C′ 三、解答题: 1.(2009辽宁朝阳)一艘小船从码头出发,沿北偏东方向航行,航行一段时间到达小岛处后,又沿着北偏西方向航行了10海里到达处,这时从码头测得小船在码头北偏东的方向上,求此时小船与码头之间的距离(,结果保留整数). 2.(2009眉山)海船以5海里/小时的速度向正东方向行驶,在A处看见灯塔B在海船的北偏东60°方向,2小时后船行驶到C处,发现此时灯塔B在海船的北偏西45方向,求此时灯塔B到C处的距离. 【关键词】解直角三角形 3.(2009眉山)计算: 【关键词】三角函数与实数运算 【答案】解:原式 4.(2009年南充)如图6,在平面直角坐标系中,已知点,轴于A. (1)求的值; (2)将点B绕原点逆时针方向旋转90°后记作点,求点的坐标; (3)将平移得到,点A的对应点是,点的对应点的坐标为 ,在坐标系中作出,并写出点.的坐标. O x A B 1 1 y 5.(2009年湖州)(1)计算: 【关键词】实数的运算 【答案】(1)解:原式==3. 6.(2009年温州)如图,△ABC中,∠C=90°,AB=8,cosA=,则AC的长是 7.(2009年温州)如图,在平面直角坐标系中,点A(,0),B(3,2),(0,2).动点D以每秒1个单位的速度从点0出发沿OC向终点C运动,同时动点E以每秒2个单位的速度从点A出发沿AB向终点B运动.过点E作EF上AB,交BC于点F,连结DA.DF.设运动时间为t秒. (1)求∠ABC的度数; (2)当t为何值时,AB∥DF; (3)设四边形AEFD的面积为S.①求S关于t的函数关系式; ②若一抛物线y=x2+mx经过动点E,当S<2时,求m的取值范围(写出答案即可). 【关键词】平面直角坐标系,动点问题,三角函数,平行线的性质,一次函数解析式的确定,二次函数的性质等综合题目 【答案】 解:(1)过点B作BM⊥x轴于点M, ∵C(0,2),B(3,2), ∴BC∥OA, ∵BM=2,AM=2, ∴tan∠BAM=, ∴∠ABC=∠BAM=30°. (2)∵AB∥DF, ∴∠CFD=∠CBA=30°, 在Rt△DCF中,CD=2-t,∠CFD=30°, ∴CF=(2-t), ∵AB=4, ∴BE=4-2t,∠FBE=30°, ∴BF=, ∴(2-t)+=3,∴t=. (3)①解法一:过点EG⊥x轴于点G,则EG=t,OG=+t ∴E(+t,t)∴DE∥x轴 S=S△DEF+ S△DEA=DE×CD+DE×OD=DE×OC =×(t+)×2=t+. 解法二:∵BF= ∴CF=3-= ∴S= S梯形OABC- S△COA -S△CDF- S△FEB =4-t-(2-t)(4t+1)-(4-2t)2 =t+. ②当S<2时,t+<2 ∴t<1 ∵t>0 ∵0查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档