2021高考数学人教版一轮复习多维层次练:第三章 第2节第1课时 导数与函数的单调性
www.ks5u.com
多维层次练17
[A级 基础巩固]
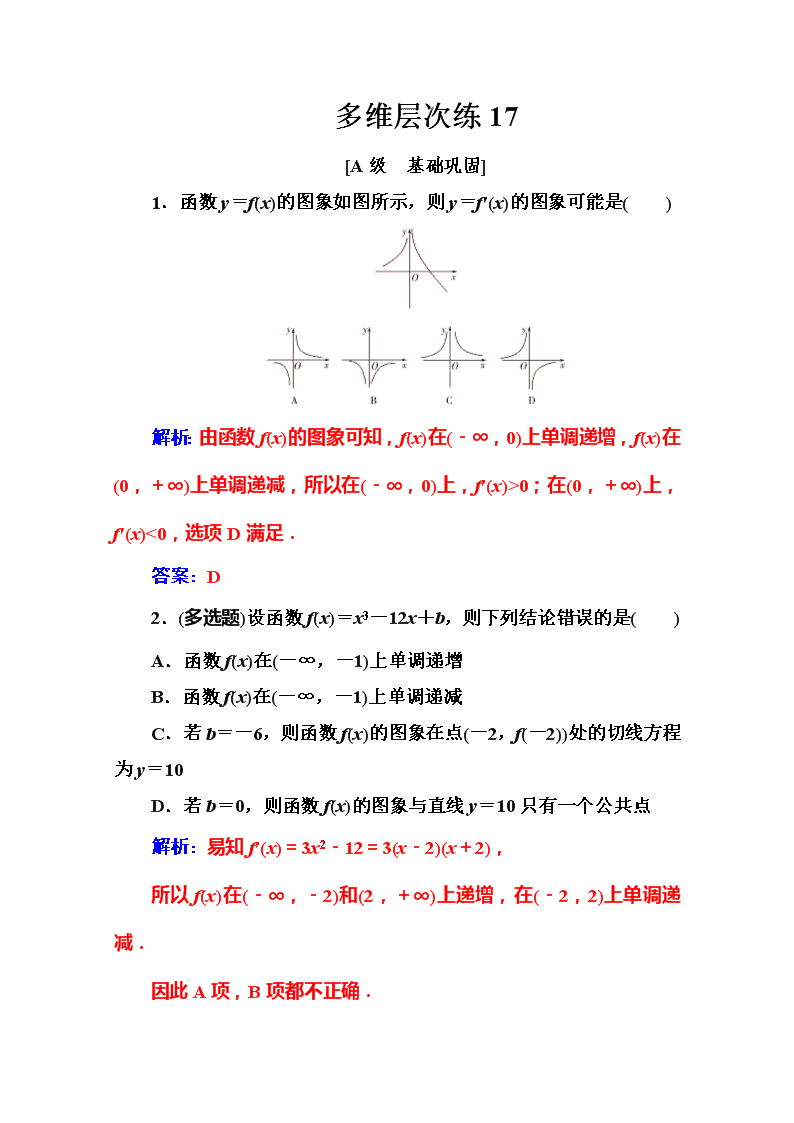
1.函数y=f(x)的图象如图所示,则y=f′(x)的图象可能是( )
解析:由函数f(x)的图象可知,f(x)在(-∞,0)上单调递增,f(x)在(0,+∞)上单调递减,所以在(-∞,0)上,f′(x)>0;在(0,+∞)上,f′(x)<0,选项D满足.
答案:D
2.(多选题)设函数f(x)=x3-12x+b,则下列结论错误的是( )
A.函数f(x)在(-∞,-1)上单调递增
B.函数f(x)在(-∞,-1)上单调递减
C.若b=-6,则函数f(x)的图象在点(-2,f(-2))处的切线方程为y=10
D.若b=0,则函数f(x)的图象与直线y=10只有一个公共点
解析:易知f′(x)=3x2-12=3(x-2)(x+2),
所以f(x)在(-∞,-2)和(2,+∞)上递增,在(-2,2)上单调递减.
因此A项,B项都不正确.
易求f′(-2)=0,当b=-6时,f(x)在x=-2处的切线为y=10,C正确.
作出函数f(x)=x3-12x(b=0)与y=10的图象,有三个交点,D
不正确.
答案:ABD
3.(2020·深圳中学调研)设函数f(x)=x2-9ln x在区间[a-1,a+1]上单调递减,则实数a的取值范围是( )
A.(1,2] B.[4,+∞)
C.(-∞,2] D.(0,3]
解析:易知f(x)的定义域为(0,+∞),且f′(x)=x-.
因为函数f(x)在区间[a-1,a+1]上单调递减,所以f′(x)≤0在[a-1,a+1]上恒成立,即0
0时,xf′(x)-f(x)<0,若a=,b=,c=,则a,b,c的大小关系正确的是( )
A.a0时,xf′(x)-f(x)<0,
所以g′(x)<0.
所以g(x)在(0,+∞)上是减函数.
由f(x)为奇函数,知g(x)为偶函数,则g(-3)=g(3),
又a=g(e),b=g(ln 2),c=g(-3)=g(3),
所以g(3)0).
令y′>0,得1-ln x>0,所以00时,有<0恒成立,则不等式x2f(x)>0的解集是________.
解析:因为当x>0时,′=<0,
所以φ(x)=在(0,+∞)上为减函数,又φ(2)=0,
所以在(0,+∞)上,当且仅当00,
此时x2f(x)>0.
又f(x)为奇函数,所以h(x)=x2f(x)也为奇函数.
故x2f(x)>0的解集为(-∞,-2)∪(0,2).
答案:(-∞,-2)∪(0,2)
9.已知函数f(x)=ax+ln x(a∈R).
(1)若a=2,求曲线y=f(x)在x=1处的切线方程;
(2)求f(x)的单调区间.
解:(1)由已知得f′(x)=2+(x>0),f′(1)=2+1=3,所以切线斜率k=3,
又切点坐标为(1,2),所以切线方程为y-2=3(x-1),
即3x-y-1=0,
故曲线y=f(x)在x=1处的切线方程为3x-y-1=0.
(2)由已知得f′(x)=a+=(x>0),
①当a≥0时,由于x>0,故ax+1>0,f′(x)>0,
所以f(x)的单调递增区间为(0,+∞).
②当a<0时,由f′(x)=0,得x=-.
在区间上,f′(x)>0,在区间上,f′(x)<0,
所以函数f(x)的单调递增区间为,单调递减区间为.
10.设函数f(x)=ax2-a-ln x,g(x)=-,其中a∈R,e=2.718…为自然对数的底数.
(1)讨论f(x)的单调性;
(2)证明:当x>1时,g(x)>0.
(1)解:由题意得f′(x)=2ax-=(x>0).
当a≤0时,f′(x)<0,f(x)在(0,+∞)内单调递减.
当a>0时,由f′(x)=0有x=,
当x∈时,f′(x)<0,f(x)单调递减;
当x∈时,f′(x)>0,f(x)单调递增.
(2)证明:令s(x)=ex-1-x,则s′(x)=ex-1-1.
当x>1时,s′(x)>0,所以s(x)>s(1),即ex-1>x,
从而g(x)=-=>0.
[B级 能力提升]
11.(2020·雅礼中学质检)已知函数f(x)=sin 2x+4cos x-ax在R上单调递减,则实数a的取值范围是________.
解析:f′(x)=2cos 2x-4sin x-a=2(1-2sin2x)-4sin x-a=-4sin2x-4sin x+2-a=-(2sin x+1)2+3-a.
由题设,f′(x)≤0在R上恒成立,
因此a≥3-(2sin x+1)2恒成立,则a≥3.
答案:[3,+∞)
12.已知函数f(x)=xsin x+cos x+x2,则不等式f(ln x)+f <2f(1)的解集为________.
解析:f(x)=xsin x+cos x+x2是偶函数,
所以f =f(-ln x)=f(ln x).
则原不等式可变形为f(ln x)0,得x>0时,f′(x)>0.
所以f(x)在(0,+∞)上单调递增.
所以|ln x|<1⇔-12时,f′(x)>0,f(x)单调递增;
当10时恒成立,
所以a≤(x2-2x)=(x-1)2-恒成立.
令φ(x)=(x-1)2-,x∈(0,+∞),则其最小值为-.
所以当a≤-时,g′(x)≥0在(0,+∞)上恒成立.
又当a=-时,g′(x)=,
当且仅当x=1时,g′(x)=0.
故当a∈时,g(x)=f(x)-ax在(0,+∞)上单调递增.
[C级 素养升华]
14.已知函数f(x)=x3+mx2+nx-2的图象过点(-1,-6),函数g(x)=f′(x)+6x的图象关于y轴对称.则m=________,f(x)的单调递减区间为________.
解析:由f(x)的图象过点(-1,-6),得m-n=-3.①
又g(x)=f′(x)+6x=3x2+(2m+6)x+n为偶函数,
所以2m+6=0,即m=-3.②
代入①式,得n=0,
所以f(x)=x3-3x2-2,则f′(x)=3x2-6x,
令f′(x)<0,得0
查看更多