- 2021-04-19 发布 |
- 37.5 KB |
- 14页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
华师版数学八年级上册课件-第14章-14勾股定理
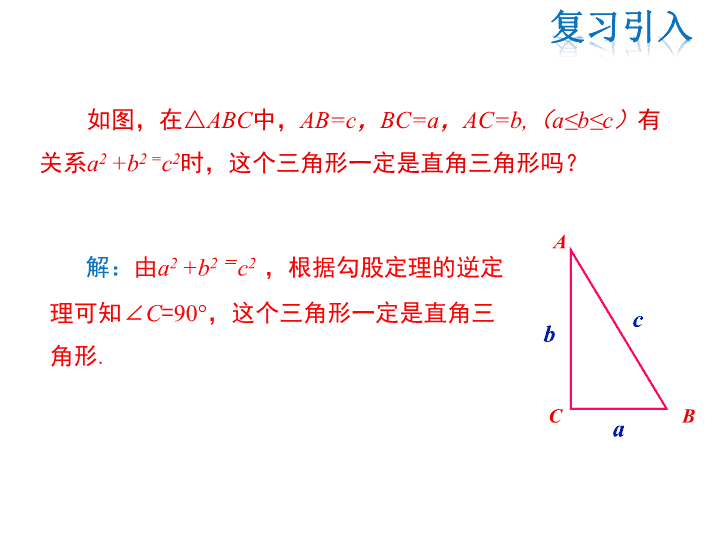
第14章 勾股定理 14.1 勾股定理 14.1.3 反证法 如图,在△ABC中,AB=c,BC=a,AC=b,(a≤b≤c) 有关系a2 +b2 =c2时,这个三角形一定是直角三角形吗? c a b A C B 解:由a2 +b2 =c2 ,根据勾股定理的逆定 理可知∠C=90°,这个三角形一定是直角三 角形. 【问题】若将上面的条件改为“在△ABC中,AB=c, BC=a,AC=b(a≤b≤c),a2 +b2 ≠ c2”,请问这个三角形是否 一定不是直角三角形呢?请说明理由. c a b A C B 【探究】 (1)假设它是一个直角三角形; (2)由勾股定理,一定有a2 +b2 =c2,与已 知条件a2 +b2 ≠ c2矛盾; (3)因此假设不成立,即它不是一个直角 三角形. 反证法 这种证明方法与前面的证明方法不同,其步骤为: (1)先假设结论的反面是正确的; (2)然后通过逻辑推理,得出与基本事实、已证的定理、 定义或已知条件相矛盾; (3)从而说明假设不成立,进而得出原结论正确. 像这样的证明方法叫“反证法”. 【例1】 写出下列各结论的反面: (1)a∥b; (2)a≥0; (3)b是正数; (4)a⊥b. a<0 b是0或负数 a不垂直于b a不平行于b 【例2】在△ABC中,AB≠AC,求证:∠B ≠ ∠ C. A B C 证明:假设 , 则 ( ), 这与 矛盾, 假设不成立, ∴ . ∠B = ∠C AB=AC 等角对等边 已知AB≠AC ∠B ≠ ∠ C 小结: 反证法的步骤:假设结论的反面成立→逻辑推理得 出矛盾→肯定原结论正确 【例3】 求证:两条直线相交只有一个交点. 已知:如图,两条相交直线a、b. 求证:a与b只有一个交点. a b A● A'● 分析:想从已知条件“两条相交直线a、b”出发,经过推 理,得出结论“a、b只有一个交点”是很困难的,因此可 以考虑用反证法. 证明:假设a与b不止一个交点,不妨假设有两个交点A和A', 因为两点确定一条直线,即经过点A和A’的直线有且只有一 条,这与已知两条直线矛盾,假设不成立. 所以两条直线相交只有一个交点. 小结:根据假设推出结论除了可以与已知条件矛盾以外, 还可以与我们学过的基本事实、定理矛盾. 【例4】 求证:在一个三角形中,至少有一个内角小于或等于 60°. 已知:△ABC. 求证:△ABC中至少有一个内角小于或等于60°. 证明:假设 , 即 , ∴ , 这与 矛盾.假设不成立. ∴ . △ABC中没有一个内角小于或等于60° ∠A>60°,∠B>60°,∠C>60° 三角形的内角和为180° △ABC中至少有一个内角小于或等于60° ∠A+∠B+∠C>60°+60°+60°=180° 1.试说出下列命题的反面: (1)a是实数; (2)a大于2; (3)a小于2; (4)至少有2个; (5)最多有一个; (6)两条直线平行; 2.用反证法证明“若a2≠ b2,则a ≠ b”的第一步是 . 3.用反证法证明“如果一个三角形没有两个相等的角,那么这个 三角形不是等腰三角形”的第一步 . a不是实数 a小于或等于2 a大于或等于2 没有两个 一个也没有 两直线相交 假设a=b 假设这个三角形是等腰三角形 4.命题“三角形中最多只有一个内角是直角”的结论的 否定是( ) A.有两个内角是直角 B.有三个内角是直角 C.至少有两个内角是直角 D.没有一个内角是直角 5.否定“自然数a、b、c中恰有一个偶数”时,正确的 反设为( ) A.a、b、c都是奇数 B. a、b、c都是偶数 C. a、b、c中至少有两个偶数 D. a、b、c中都是奇数或至少有两个偶数 C D 6.已知:a是整数,2能整除a2. 求证:2能整除a. 证明:假设命题的结论不成立,即“2不能整除a”. 因为a是整数,故a是奇数. 不妨设a=2n+1(n是整数), ∴a2=(2n+1)2=4n2+4n+1=2(2n2+2n)+1, ∴a2是奇数,则2不能整除a2 ,这与已知矛盾. ∴假设不成立,故2能整除a. 原词语 否定词 原词语 否定词 等于 任意的 是 至少有一个 都是 至多有一个 大于 至少有n个 小于 至多有n个 对所有x成 立 对任何x 不成立 7.准确地作出反设(即否定结论)是非常重要的,下面是 一些常见的关键词的否定形式. 不是 不都是 不大于 不小于 一个也没有 至少有两个 至多有(n-1)个 至少有(n+1)个 存在某个x 不成立 存在某个x成立 不等于 某个 反证法 概念 反证法证明的思路:假设命题不成 立→正确的推理,得出矛盾→肯定待 定命题的结论 证明步骤查看更多