2017-2018学年广西省贵港市覃塘高级中学高二下学期5月月考数学（理）试题（Word版）

2017-2018学年广西省贵港市覃塘高级中学高二下学期5月月考数学（理）试题（Word版）

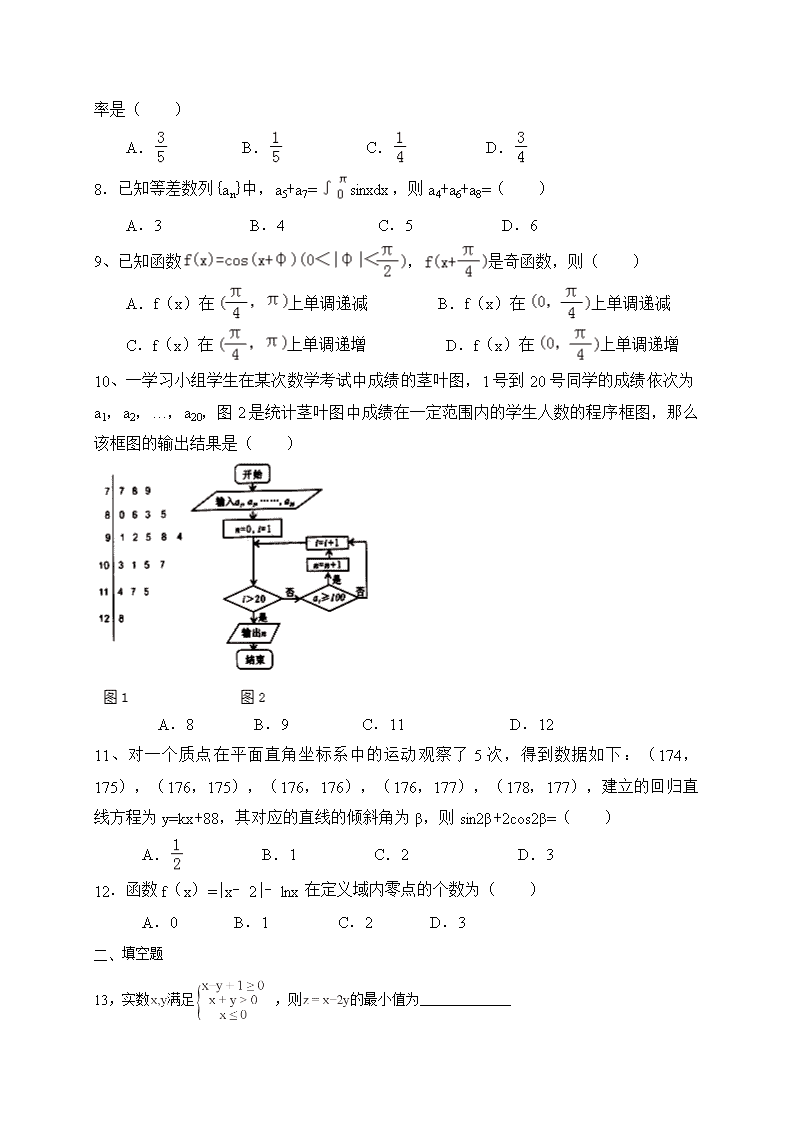
覃塘高中2018年春季期5月月考试题 高二理科数学 ‎ ‎ 试卷说明：本试卷分Ⅰ卷和Ⅱ卷，Ⅰ卷为试题（选择题和客观题），学生自已保存，Ⅱ卷一般为答题卷，考试结束只交Ⅱ卷。‎ 一、选择题（本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项符合题目的要求）‎ ‎1．已知集合A={x|x2﹣x﹣6＜0}，B={x|3x＞1}，则A∩B=（　　）‎ A．（1，2） B．（1，3） C．（0，2） D．（0，3）‎ ‎2、坐标系中，若角α的终边经过点，则sin（π+α）=（　　）‎ A． B． C． D．‎ ‎3. 已知函数为奇函数，则f（g（﹣3））=（　　）‎ A．﹣3 B．﹣‎2 ‎C．﹣1 D．0‎ ‎4、直线l被圆x2+y2﹣2x﹣4y=0平分，且与直线x+2y=0垂直，则直线l的方程是（　　）‎ A．2x﹣y=0 B．2x﹣y﹣2=‎0 ‎C．x+2y﹣3=0 D．x﹣2y+3=0‎ ‎5、边长为1的正方形组成的网格中，画出的是一个几何体的三视图，则几何体的体积是（　　）‎ A．9 B． C．18 D．27‎ ‎6、已知a=log52，b=log73，c=log3，则a，b，c的大小关系（　　）‎ A．a＜b＜c B．a＜c＜b C．b＜a＜c D．c＜b＜a ‎7，在区间1，5]随机地取一个数m，则方程m2x2+4y2‎ ‎=1表示焦点在y轴上的椭圆的概率是（　　）‎ A． B． C． D．‎ ‎8．已知等差数列{an}中，a5+a7=sinxdx，则a4+a6+a8=（　　）‎ A．3 B．‎4 ‎C．5 D．6‎ ‎9、已知函数，是奇函数，则（　　）‎ A．f（x）在上单调递减 B．f（x）在上单调递减 C．f（x）在上单调递增 D．f（x）在上单调递增 ‎10、一学习小组学生在某次数学考试中成绩的茎叶图，1号到20号同学的成绩依次为a1，a2，…，a20，图2是统计茎叶图中成绩在一定范围内的学生人数的程序框图，那么该框图的输出结果是（　　）‎ A．8 B．‎9 ‎C．11 D．12‎ ‎11、对一个质点在平面直角坐标系中的运动观察了5次，得到数据如下：（174，175），（176，175），（176，176），（176，177），（178，177），建立的回归直线方程为y=kx+88，其对应的直线的倾斜角为β，则sin2β+2cos2β=（　　）‎ A． B．‎1 ‎C．2 D．3‎ ‎12．函数f（x）=|x﹣2|﹣lnx在定义域内零点的个数为（　　）‎ A．0 B．‎1 ‎C．2 D．3‎ 二、 填空题 ‎13，实数满足，则的最小值为_____________‎ ‎14、已知平面向量，满足||=3，||=2，与的夹角为120°，若（+m）⊥，则实数m的值为____________‎ ‎15，ABC的内角A，B，C的对边分别为a，b，c，（a+b+c）（a﹣b+c）=ac，则B=　 ‎ ‎16．已知函数f(x)＝(ax2＋x)－xlnx在[1，＋∞)上单调递增，则实数a的取值范围是________。‎ 三、解答题 ‎17. 已知函数．‎ ‎（1）求函数f（x）的单调递减区间；‎ ‎（2）若△ABC的内角A，B，C所对的边分别为a，b，c，，，sinB=2sinC，‎ 求c．‎ ‎18、某校从参加高一年级期末考试的学生中抽出40名学生，将其成绩（均为整数）分成六段，[40，50），[50，60），…[90，100]后画出如下部分频率分布直方图，观察图形的信息，回答下列问题：‎ ‎（1）求第四小组的频率，并补全频率分布直方图；‎ ‎（2）估计这次考试的及格率（60分及以上为及格）和平均分；‎ ‎（3）从成绩是40～50分及90～100分的学生中选两人，记他们的成绩为x，y，求满足“|x﹣y|＞‎10”‎的概率．‎ ‎19.等差数列{an}中，a2=4，其前n项和Sn满足．‎ ‎（1）求实数λ的值，并求数列{an}的通项公式；‎ ‎（2）若数列是首项为λ、公比为2λ的等比数列，求数列{bn}的前n项的和Tn．‎ ‎20．如图，在四棱锥P﹣ABCD中，底面是边长为a的正方形，侧棱PD=a，PA=PC=a．‎ ‎（1）求证：PD⊥平面ABCD；‎ ‎（2）求证：平面PAC⊥平面PBD；‎ ‎（3）求证：∠PCD为二面角P﹣BC﹣D的平面角．‎ ‎21已知函数y=+lg（﹣x2+4x﹣3）的定义域为M，‎ ‎（1）求M；‎ ‎（2）当x∈M时，求函数f（x）=a•2x+2+3•4x（a＜﹣3）的最小值．‎ ‎22、已知椭圆C：+=1（a＞b＞0）的左、右焦点分别为F1、F2，右顶点为A，上顶点为B，△BF‎1F2是边长为2的正三角形．‎ ‎（1）求椭圆C的标准方程及离心率；‎ ‎（2）是否存在过点F2的直线l，交椭圆于两点P、Q，使得PA∥QF1，如果存在，试求直线l的方程，如果不存在，请说明理由．‎ 高二理数答案 ‎1．已知集合A={x|x2﹣x﹣6＜0}，B={x|3x＞1}，则A∩B=（　　）‎ A．（1，2） B．（1，3） C．（0，2） D．（0，3）‎ ‎【解答】解：集合A={x|x2﹣x﹣6＜0}={x|﹣2＜x＜3}，‎ B={x|3x＞1}={x|x＞0}，‎ ‎∴A∩B={x|0＜x＜3}=（0，3）．‎ 故选：D．‎ ‎2、坐标系中，若角α的终边经过点，则sin（π+α）=（　　）‎ A． B． C． D．‎ ‎【解答】解：∵角α终边经过点，即点P（，），‎ ‎∴x=，y=，r=|OP|=1，‎ 则sin（π+α）=﹣sinα==﹣y=﹣．‎ 故选：A．‎ ‎3. 已知函数为奇函数，则f（g（﹣3））=（　　）‎ A．﹣3 B．﹣‎2 ‎C．﹣1 D．0‎ ‎【解答】解：函数为奇函数，‎ f（g（﹣3））=f[﹣（log33﹣2）]‎ ‎=f（1）=log31﹣2=0﹣2=﹣2．‎ 故选：B．‎ ‎4、直线l被圆x2+y2﹣2x﹣4y=0平分，且与直线x+2y=0垂直，则直线l的方程是（　　）‎ A．2x﹣y=0 B．2x﹣y﹣2=‎0 ‎C．x+2y﹣3=0 D．x﹣2y+3=0‎ ‎【解答】解：设与直线l：x+2y=0垂直的直线方程：2x﹣y+b=0，‎ 圆C：x2+y2﹣2x﹣4y=0化为（x﹣1）2+（y﹣2）2=5，圆心坐标（1，2）．‎ 因为直线平分圆，圆心在直线2x﹣y+b=0上，所以2×1﹣1×2+b=0，解得b=0，[来源:学#科#网 故所求直线方程为2x﹣y=0．‎ 故选：A．‎ ‎5、边长为1的正方形组成的网格中，画出的是一个几何体的三视图，则该几何体的体积是（　　）‎ A．9 B． C．18 D．27‎ ‎【解答】解根据三视图可知几何体是一个三棱锥A﹣BCD，‎ 三棱锥的外面是长、宽、高为6、3、3的长方体，‎ ‎∴几何体的体积V==9，‎ 故选：A．‎ ‎　‎ ‎6、已知a=log52，b=log73，c=log3，则a，b，c的大小关系（　　）‎ A．a＜b＜c B．a＜c＜b C．b＜a＜c D．c＜b＜a ‎【解答】解：∵c=log3=log53＞log73，‎ b=log73＞=，a=log52＜=，‎ 则a，b，c的大小关系为：a＜b＜c．‎ 故选：A．‎ ‎7，在区间1，5]随机地取一个数m，则方程m2x2+4y2=1表示焦点在y轴上的椭圆的概率是（　　）‎ A． B． C． D．‎ ‎【解答】解：若方程m2x2+4y2=1表示焦点在y轴上的椭圆，‎ 则m2＞4，解得：m＞2，‎ 故满足条件的概率是p==，‎ 故选：D．‎ ‎8．已知等差数列{an}中，a5+a7=sinxdx，则a4+a6+a8=（　　）‎ A．3 B．‎4 ‎C．5 D．6‎ ‎【解答】解：等差数列{an}中，a5+a7=sinxdx=（﹣cosx）|=﹣（﹣1﹣1）=2，‎ 可得a4+a8=‎2a6=a5+a7=2，‎ 则a4+a6+a8=3，‎ 故选：A．‎ ‎9、已知函数，是奇函数，则（　　）‎ A．f（x）在上单调递减 B．f（x）在上单调递减 C．f（x）在上单调递增 D．f（x）在上单调递增 ‎【解答】解：函数f（x）=cos（x+φ），‎ ‎∴=cos（x+φ+），‎ 又f（x+）是奇函数，‎ ‎∴φ+=+kπ，k∈Z，‎ ‎∴φ=+kπ，k∈Z；‎ 又0＜|φ|＜，‎ ‎∴φ=，‎ ‎∴f（x）=cos（x+），‎ 当x∈（0，）时，x+∈（，），f（x）是单调减函数；‎ x∈（，π）时，x+∈（，），f（x）先减后增．‎ 故选：B．‎ ‎　‎ ‎10、一学习小组学生在某次数学考试中成绩的茎叶图，1号到20号同学的成绩依次为a1，a2，…，a20，图2是统计茎叶图中成绩在一定范围内的学生人数的程序框图，那么该框图的输出结果是（　　）‎ A．8 B．‎9 ‎C．11 D．12‎ ‎【解答】解：根据茎叶图知，这20名同学的成绩依次为a1，a2，…，a20，‎ 分析程序框图知，该程序运行后输出成绩大于或等于100的人数，‎ 由此知输出的结果是8．‎ 故答案为：8．‎ 故选：A．‎ ‎11、对一个质点在平面直角坐标系中的运动观察了5次，得到数据如下：（174，175），（176，175），（176，176），（176，177），（178，177），建立的回归直线方程为y=kx+88，其对应的直线的倾斜角为β，则sin2β+2cos2β=（　　）‎ A． B．‎1 ‎C．2 D．3‎ ‎【解答】解：由题意，=×（174+176+176+176+178）=176，‎ ‎=×（175+175+176+177+177）=176，‎ ‎∵回归直线方程为y=kx+88，‎ ‎∴176=176k+88，‎ ‎∴k=，‎ ‎∵直线的倾斜角为β，‎ ‎∴tanβ=，‎ ‎∴sin2β+2cos2β=+‎ ‎=+=+=2，‎ 故选：C．‎ ‎　‎ ‎12．函数f（x）=|x﹣2|﹣lnx在定义域内零点的个数为（　　）‎ A．0 B．‎1 ‎C．2 D．3‎ ‎【解答】解：由题意，函数f（x）的定义域为（0，+∞）；‎ 由函数零点的定义，f（x）在（0，+∞）内的零点即是方程|x﹣2|﹣lnx=0的根．‎ 令y1=|x﹣2|，y2=lnx（x＞0），在一个坐标系中画出两个函数的图象：‎ 由图得，两个函数图象有两个交点，‎ 故方程有两个根，即对应函数有两个零点．‎ 故选：C．‎ ‎13，实数满足，则的最小值为_____________‎ ‎【答案】‎ ‎【解析】根据已知作出可行域如图所示：‎ ‎，即，斜率为，在处截取得最小值为 ‎14、已知平面向量，满足||=3，||=2，与的夹角为120°，若（+m）⊥，则实数m的值为____________‎ ‎【解答】解：∵||=3，||=2，与的夹角为120°，‎ ‎∴=cos120°==﹣3．‎ ‎∵（+mb）⊥，‎ ‎∴（+m）•==32﹣‎3m=0，解得m=3．‎ 答案：3‎ ‎15，ABC的内角A，B，C的对边分别为a，b，c，（a+b+c）（a﹣b+c）=ac，则B=　　．‎ ‎【解答】解：△ABC的内角A，B，C的对边分别为a，b，c，‎ ‎∵（a+b+c）（a﹣b+c）=ac，即a2+c2﹣b2=﹣ac，‎ 又cosB==﹣，‎ ‎∴B=，‎ 故答案为：．‎ ‎16．已知函数f(x)＝(ax2＋x)－xlnx在[1，＋∞)上单调递增，则实数a的取值范围是________。‎ 解析：由题意知：f′(x)＝2ax＋1－(lnx＋1)≥0，即a≥在x∈[1，＋∞)上恒成立；‎ 设g(x)＝，令g′(x)＝＝0，‎ 解得x＝e，当x∈(e，＋∞)时，g′(x)＜0，‎ g(x)为减函数，当x∈[1，e)时，‎ g′(x)＞0，g(x)为增函数，‎ 故g(x)的最大值为g(e)＝，即a≥。‎ 答案：a≥ ‎17．已知函数．‎ ‎（1）求函数f（x）的单调递减区间；‎ ‎（2）若△ABC的内角A，B，C所对的边分别为a，b，c，，，sinB=2sinC，求c．‎ ‎【解答】解：（1）=，‎ 由，k∈Z，‎ 解得，k∈Z；‎ ‎∴函数f（x）的单调递减区间为，k∈Z；‎ ‎（2）∵，A∈（0，π），∴；‎ ‎∵sinB=2sinC，∴由正弦定理，得b=‎2c；‎ 又由余弦定理a2=b2+c2﹣2bccosA，，‎ 得，[]‎ 解得c=1．‎ ‎18．某校从参加高一年级期末考试的学生中抽出40名学生，将其成绩（均为整数）分成六段，[40，50），[50，60），…[90，100]后画出如下部分频率分布直方图，观察图形的信息，回答下列问题：‎ ‎（1）求第四小组的频率，并补全频率分布直方图；‎ ‎（2）估计这次考试的及格率（60分及以上为及格）和平均分；‎ ‎（3）从成绩是40～50分及90～100分的学生中选两人，记他们的成绩为x，y，求满足“|x﹣y|＞‎10”‎的概率．‎ ‎【解答】解：（1）由频率分布的直方图可得，第四小组的频率为 1﹣10（0.01+0.015+0.015+0.025+0.05）=0.3．‎ 故第四个小矩形的高为=0.03．如图所示：‎ ‎（2）由于这次考试的及格的频率为10×（0.015+0.03+0.025+0.005）=0.75，故及格率为0.75．‎ 由频率分布直方图可得平均分为 0.1×45+0.15×55+0.15×65+0.3×75+0.25×85+0.05×95=71．‎ ‎（3）由频率分步直方图可得，成绩是40～50分的有40×0.1=4人，90～100分的学生有40×0.05=2人，记取出的2个人的成绩为x，y，‎ ‎“|x﹣y|＞‎10”‎说明选出的2个人一个成绩在[40，50）内，另一个在[50，60）内，‎ 故满足“|x﹣y|＞‎10”‎的选法有 4×2=8种，而所有的取法有 =15种，‎ 故满足“|x﹣y|＞‎10”‎的概率等于 ．‎ ‎19．等差数列{an}中，a2=4，其前n项和Sn满足．‎ ‎（1）求实数λ的值，并求数列{an}的通项公式；‎ ‎（2）若数列是首项为λ、公比为2λ的等比数列，求数列{bn}的前n项的和Tn．‎ ‎【解答】解：（I）因为a2=S2﹣S1=4+2λ﹣1﹣λ=4，解得λ=1∴‎ 当n≥2时，则=2n，‎ 当n=1时，也满足，所以an=2n．‎ ‎（II）由已知数列是首项为1、公比为2的等比数列 其通项公式为，且首项，‎ 故，=2n﹣1‎ ‎=，‎ Tn=（1+21+…+2n﹣1）…﹣[（1﹣）+（）+…+（）]=2n﹣1﹣．‎ ‎20．如图，在四棱锥P﹣ABCD中，底面是边长为a的正方形，侧棱PD=a，PA=PC=a．‎ ‎（1）求证：PD⊥平面ABCD；‎ ‎（2）求证：平面PAC⊥平面PBD；‎ ‎（3）求证：∠PCD为二面角P﹣BC﹣D的平面角．‎ ‎【解答】（1）证明：∵PA=PC=a，PD=a ‎∴PD2+AD2=PA2，即PD⊥AD，‎ 又∵PD⊥CD．AD∩CD=D ‎∴PD⊥平面ABCD；‎ ‎（2）由（1）可得PD⊥AC，又四边形ABCD为正方形，所以AC⊥BD，‎ 所以 AC⊥平面PBD，‎ 所以平面PAC⊥平面PBD；‎ ‎（3）由（1）可得PD⊥BC，又BC⊥CD，所以BC⊥平面PCD，‎ 所以BC⊥CD，BC⊥PC，‎ 所以∠PCD为二面角P﹣BC﹣D的平面角．‎ ‎//‎ ‎21．已知函数y=+lg（﹣x2+4x﹣3）的定义域为M，‎ ‎（1）求M；‎ ‎（2）当x∈M时，求函数f（x）=a•2x+2+3•4x（a＜﹣3）的最小值．‎ ‎22．已知椭圆C：+=1（a＞b＞0）的左、右焦点分别为F1、F2，右顶点为A，上顶点为B，△BF‎1F2是边长为2的正三角形．‎ ‎（1）求椭圆C的标准方程及离心率；‎ ‎（2）是否存在过点F2的直线l，交椭圆于两点P、Q，使得PA∥QF1，如果存在，试求直线l的方程，如果不存在，请说明理由．‎ ‎【解答】解：（Ⅰ）椭圆C：+=1（a＞b＞0）焦点在x轴上，由△BF‎1F2是边长为2的正三角形，‎ a=2，c=1，则b2=a2﹣c2=3，…（2分）‎ ‎∴椭圆C的标准方程为，…（3分）‎ 椭圆的离心率e==；…（4分）‎ ‎（Ⅱ）解法1：由（Ⅰ）得，F1（﹣1，0），F2（1，0），A（2，0），设P（x1，y1），Q（x2，y2）．‎ 显然直线l的斜率不为零，设直线l的方程为x=my+1，‎ 则，…（5分）‎ 整理得：（‎3m2‎+4）y2+6my﹣9=0，‎ ‎△=‎36m2‎+36（‎3m2‎+4）=‎144m2‎+144＞0，‎ 由韦达定理可知：y1+y2=﹣，y1•y2=﹣，…（7分）‎ 则=（x1﹣2，y1）=（my1﹣1，y1）=（x2+1，y2）=（my2+2，y2），…（8分）‎ 若PA∥QF1，则（my1﹣1）y2=（my2+2）y1，即y2=﹣2y1，…（9分）‎ 解得：，则y1•y2=﹣，…（10分）‎ 故=，解得：‎5m2‎=4，即m=±，…（11分）‎ 故l的方程为x=y+1或x=﹣y+1，‎ 即x﹣2y﹣=0或+2y﹣=0 …（12分）‎ 解法2：由（Ⅰ）得F1（﹣1，0），F2（1，0），A（2，0），‎ 直线l⊥x时，=1≠，则PA∥QF1不成立，不符合题意．…（5分）‎ 可设直线L的方程为y=k（x﹣1）..…（6分）‎ ‎，消去y，可得（4k2+3）x2﹣8k2x+4k2﹣12=0，…（7分）‎ 则△=144（k2+1）＞0．设P（x1，y1），Q（x2，y2）．‎ 则x1+x2=﹣，①x1•x2=，②．…（8分）‎ ‎=（x1﹣2，y1），=（x2+1，y2）．‎ 若PA∥QF1，则∥，‎ 则k（x1﹣2）（x2﹣1）﹣k（x2+1）（x1﹣1）=0．‎ 化简得2x1+x2﹣3=0③．…（9分）‎ 联立①③可得x1=，x2=，…（10分）‎ 代入②可以解得：k=±．…（11分）‎ 故l的方程为x﹣2y﹣=0或+2y﹣=0．…（12分）‎ ‎　‎