2019衡水名师原创文科数学专题卷专题十二《直线与圆的方程》

2019衡水名师原创文科数学专题卷专题十二《直线与圆的方程》

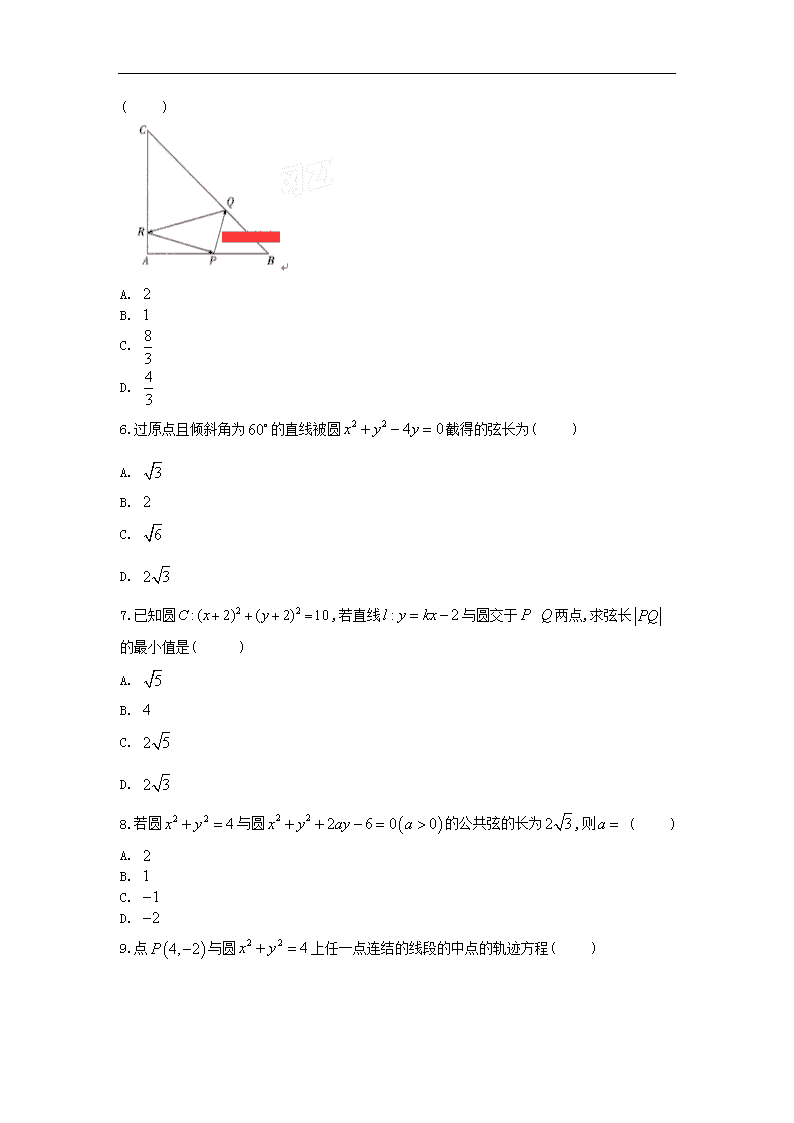
2019 衡水名师原创文科数学专题卷 专题十二 直线与圆的方程 考点 37：直线方程与两直线的的位置关系（1-5 题，13 题） 考点 38：圆的方程及点，线，圆的位置关系（6-12 题，14-16 题，17-22 题） 考试时间：120 分钟 满分：150 分 说明：请将选择题正确答案填写在答题卡上，主观题写在答题纸上 第 I 卷（选择题） 一、选择题 1.直线 3 2 0x y   的倾斜角为( ) A. 6  B. 3  C. 5 6  D. 2 3  2.斜率为 3 ,在 x 轴上截距为 2 的直线方程的一般式为( ) A. 3 6 0x y   B. 3 2 0x y   C. 3 6 0x y   D. 3 2 0x y   3.已知直线 1 0ax by   与直线 4 3 5 0 x y   平行,且在 y 轴上的截距为 1 3 ,则 a b 的 值为( ) A.7 B.-1 C.1 D.-7 4.已知直线 过点 且与点 , 等距离,则直线 的方程为( ) A. B. C. 或 D. 或 5.在等腰直角三角形 ABC 中, 4AB AC  ,点 P 是边 AB 上异于 ,  A B 的一点.光线从点 P 出发,经 ,BC CA反射后又回到点 P (如图).若光线QR 经过 ABC 的重心,则 AP 等于 ( ) A. 2 B. 1 C. 8 3 D. 4 3 6.过原点且倾斜角为 60 的直线被圆 2 2 4 0x y y   截得的弦长为( ) A. 3 B. 2 C. 6 D. 2 3 7.已知圆 2 2:( 2) ( 2) 10C x y    ,若直线 : 2l y kx  与圆交于 , P Q 两点,求弦长 PQ 的最小值是( ) A. 5 B. 4 C. 2 5 D. 2 3 8.若圆 2 2 4x y  与圆  2 2 2 6 0 0x y ay a     的公共弦的长为 2 3 ,则 a  ( ) A. 2 B. 1 C. 1 D. 2 9.点  4, 2P  与圆 2 2 4x y  上任一点连结的线段的中点的轨迹方程( ) A.    2 22 1 1x y    B.    2 22 1 4x y    C.    2 24 2 4x y    D.    2 22 1 1x y    10.若实数 ,x y 满足 2 2 2 2 1 0x y x y     则 4 2 y x   的取值范围为( ) A. 40, 3      B. 4 ,3    C. 4, 3      D. 4 ,03     11 已知过点 引直线 与曲线 相交于 两点, 为坐标原点,当 的面积取最大值时,直线 的倾斜角为( ) A.150° B.135° C.120° D.105° 12.如图,已知直线 3 34y x  与  x 轴、 y 轴分别交于 A 、B 两点, P 是以  0,1C 为圆心, 1为半径的圆上一动点,连结 PA 、 PB ,则 PAB 面积的最大值是( ) A. 8 B. 12 C. 21 2 D. 17 2 二、填空题 13.设点  1,0A ﹣ ,  2,1B ,若直线 1 0ax by   与线段 AB 有一个公共点,则 2 2a b 的最 小值为__________. 14.曲线 lny x 上的点到直线 2 3 0x y   的最短距离是__________. 15.过原点  O 作圆 2 2 6 8 20 0x y x y     的两条切线,设切点分别为 , P Q ,则线段 P Q、 的长为__________ 16.直线 1: 1 0l ax ya    与  x , y 轴的交点分别为 A 、 B ,直线l 与圆 2 2: 1O x y  的交 点为C , D .给出下面三个结 论:① 1a  , 1 2AOBS  ;② 1|a  ,  AB CD ;③ 1|a  , 1 2CODS  ,则所有正确结 论的序号是__________. 三、解答题 17.从点引圆 1C :的切线 P Q、 ,切点为 Q . 1.当 m 变化时,求切点Q 的轨迹C 的方程 2.已知直线 :(1 2 ) (1 ) 5 4 0l k x k y k      ( )k R ,求证:直线l 与轨迹 C 恒相交,并求 出相交的弦长最短时的直线l 的方程. 18.在平面直角坐标系 xOy 中,直线 1 0x y   截以原点O 为圆心的圆所得的弦长为 6 . 1.求圆 O 的方程; 2.若直线l 与圆O 切于第一象限,且与坐标轴交于点 D , E ,当 DE 长最小时,求直线l 的方 程; 3.设 M , P 是圆O 上任意两点,点 M 关于 x 轴的对称点为 N ,若直线 M PØ , NP 分别交 x 轴于点  ,0m 和 ( ,0)n ,问 m n、 是否为定值?若是,请求出定值;若不是,请说明理由. 19.已知圆 M 与圆 N : 2 2 25 5 3 3x y r             关于直线 y x 对称,且点 1 5,3 3D    在 圆 M 上. 1.判断圆 M 与圆 N 的位置关系; 2.设 P 为圆 M 上任意一点, 51, 3A    , 51, 3B     , PA  与 PB  不共线, PG 为 APB 的平 分线,且交 AB 于G ,求证 PBG 与 APG 的面积之比为定值. 20.已知圆 2 2: 2 4 3 0.C x y x y     1.若圆 C 的切线在 x 轴和 y 轴上的截距相等,求此切线的方程. 2.从圆 C 外一点  1 1,P x y 向该圆引一条切线,切点为 ,M O 为坐标原点,且有 ,PM PO 求使得 PM 取得最小值的点 P 的坐标. 21.已知点  0 0,M x y 在圆 2 2: 4O x y  上运动,且存在一定点  6,0N ,点  ,P x y 为线 段 MN 的中点. 1.求点 P 的轨迹C 的方程; 2.过  0,1A 且斜率为 k 的直线l 与点 P 的轨迹C 交于不同的两点 ,E F ,是否存在实数 k 使 得 12OE OF   ,并说明理由. 22.已知直线 1l : 2 2 0mx y m    , 2l : 2 2 0x my m    , 1l 与 y 轴交于 A 点, 2l 与 x 轴交于 B 点, 1l 与 2l 交于 D 点,圆 C 是 ABD 的外接圆. 1.判断 ABD 的形状并求圆 C 面积的最小值. 2.若 D , E 是抛物线 2 2x py 与圆 C 的公共点,问:在抛物线上是否存在点 P 使得 PDE 是等腰三角形?若存在,求点 P 的个数;若不存在,请说明理由. 参考答案 一、选择题 1.答案：C 解析： 2.答案：A 解析： 3.答案：D 解析： 4.D 设所求直线的方程为 ,即 , 由已知及点到直线的距离公式可得 , 解得 或 , 即所求直线方程为 或 . 5.答案：D 解析：以 AB 为 x 轴, AC 所在直线为 y 轴建立如图所示的坐标系, 由题可知      4,0 , 0,4 , 0,0B C A , 则直线 BC 方程为 4 0x y   , 设 ( ,0)(0 4)P t t  ,由对称知识可得点 P 关于直线 BC 的对称点 1P 的坐标为 4,4 t ,点 P 关于 y 轴的对称点 2P 的坐标为 ( ,0)t ,根据反射定理可知 1 2PP 就是光线 RQ 所在直线. 由 1P 、 2P 两点坐标可得直线 1 2PP 的方程为 4 ( )4 ty x tt   ,设 ABC 的重心为G ,易知 4 4,3 3G     .因为重心 4 4,3 3G     在光线 RQ 上,所以有 4 4 4 3 4 3 t tt        ,即 23 4 0t t  .所 以 0t  或 4 3t  ,因为 0 4t  ,所以 4 3t  ,即 4 3AP  ,故选 D. 6.答案：D 解析：由已知得直线的方程为 3y x 圆心为 0,2 ,半径 2r  .由点到直线的距离公式得 弦心距等于1,从而所求弦长等于 2 22 2 1 2 3  故选 D. 7.答案：C 解析： 8.答案：B 解析： 9.答案：A 解析：设中点坐标为  ,A x y ,那么圆上一点设为  ', 'B x y ,满足 ' 4 2{ ' 2 2 x x y y     , ' 2 4{ ' 2 2 x x y y     ,根据条件 2 2' ' 4x y  , 代入后得到   2 22 4 2 2 4x y    , 化简为:   2 22 1 1x y    ,故选 A. 10.答案：B 解析：原方程配方得   2 21 1 1x y    , 4 2 y x   表示的是圆上的点和点 2,4 之间的连线 的斜率,画出图象如下图所示,结合选项和图象可知,斜率的最小值为 4 3 ,没有最大值. 答案： A 解析： 由题意知直线的斜率必然存在,设直线的斜率为 且 , 则直线方程为 ,设圆心到直线的距离为 ,则 , , 可用二次函数,也可根据基本不等式 , (当且仅当 即 时,等号成立), 此时三角形的面积最大,且 ,解得 , 则倾斜角为 150°,选 A. 12.答案：C 解析：因为直线 3 34y x  与  x 轴、 y 轴分别交于 A 、 B 两点两点, 所以 (4,0)A , (0, 3)B  ,即 4OA  , 3OB  ,所以 5AB  . 根据题意分析可得要 PAB 面积的最大则点 P 到直线 AB 的距离最远, 所以点 P 在过点C 的 AB 的垂线上,过点C 作  CD AB 于点 D , 易证 BCD BAO   ,所以 BC CD BA AO  ,所以 4 5 4 CD , 所以 16 5CD  ,所以点 P 到直线 AB 的距离为 16 211 5 5   , 所以 PAB 面积的最大值为 1 21 2152 5 2    ,故选 C. 二、填空题 13.答案： 1 5 解析：因为直线 1 0ax by   与线段 AB 有一个公共点, 所以点  1,0A ﹣ ,  2,1B 在直线 1 0ax by   的两侧, 所以  1 2 1 0a a b    ,即 1 0{2 1 0 a a b      或 1 0{2 1 0 a a b      ,画出它们表示的平面区域,如图所示, 2 2a b 表示原点到区域的点距离的平方,由图可知, 当原点  O 到直线 2 1 0x y   的距离到区域内的点的距离的最小值, 1 1 4 1 5 d    ,所以 2 2a b 的最小值 2 1 5d  . 14.答案：  5 4 ln 2 5  解析：设点  0 0,P x y 到直线 2 3 0x y   的距离最短,所以曲线在点  0 0,P x y 处的切线 斜率为 2 ,而 1y x   ,所以 0 1 2x  ∴ 0 0 1 1, ln2 2x y  根据点到直线的距离公式可知曲线上的点到直线的最短 距离为  5 4 ln 2 5  考点: 本小题主要考查曲线上的点到直线的距离的最值,导数的计算等. 点评: 解决本小题的关键是找出曲线在所求的点处的切线与已知直线平行,所以斜率相等,进而利 用导数计算. 15.答案：4 解析： 16.答案：①③ 解析：①当 1a  时,分别可得直线的截距,由三角形的面积公式易得结论①正确; ②当 1a  时,反证法可得结论②错误;③由三角形的面积公式可得 1 1sin2 2CODS AOC    ,可得结论③正确. ①当 1a  时,把 0x  代入直线方程可得 y a , 把 0y  代入直线方程可得 1x a  ,∴ 1 1 1 2 2AOBS a a     ,故结论①正确; ②当 1a  时, 2 2 1AB a a   ,∴ 2 2 2 1AB a a   , 直线l 可化为 2 0a x y a   ,圆心 O 到l 的距离 4 4 2 2 1 11 1 a ad a a a a       ,  2 2 2 2 14 1 4 1 1CD d a a            ,假设  AB CD ,则 2 2AB CD , 即 2 2 2 2 1 14 1 1a a a a           ,∴ 2 2 2 2 2 1 14 4 0a aa a               ,∴ 2 2 2 1 2 0a a       , 显然矛盾,故结论②错误; 1 1 1sin sin2 2 2CODS OD OC COD COD      , ∴ 1a  , 1 2CODS  ,所以结论③正确. 三、解答题 17.答案：1. 2 2( 2) 8x y   2.直线 l 的方程可化为 ( 2 4) 5 0k x y x y       ,l 可看作是过直线 2 4 0x y    和 5 0x y   的交点 (3,2) 的直线系, 即l 恒过定点 (3,2)Q ,由 2 2(3 2) 2 5 8    知点Q 在圆 P 内, 所以 l 与圆 P 恒相交, 设l 与圆 P 的交点为 ,M N ,则 22 8MN d  ( d 为 P 到l 的距离),设 P Q、 与l 的夹角为 ,则 sin 5 sind PQ     ,当 90   时, d 最大, MN 最短,此时l 的斜率为 P Q、 的斜率的负倒数 1 2  ,故l 的方程为 12 ( 3)2y x    , 2 7 0x y   解析： 18.答案：1.圆心  0,0O 到直线 1 0x y   的距离 0 0 1 2 22 d    , 又半弦长 6 2 ,则该圆的半径 1 6 22 4r    , 所以圆O 的方程为 2 2 2x y  . 2.设直线  : 1 0, 0x yl a ba b     ,即 0bx ay ab   , 则  ,0D a ,  0,E b ,由题设可得 2 2 2ab a b   , 即    22 22 a b ab  ,又因   22 2 2 2 a bab      , 故   22 2 2 22 2 a ba b       ,即 2 2 8a b  , 故 2 2 2 2DE a b   (当且仅当 2a b  时取等号), 此时所求直线l 的方程为 2 0x y   . 3.设  1 1,M x y ,  0 0,P x y ,由题意得  1 1,N x y ,则 0 1 0 1 MP y yk x x   , 直线  0 1 0 0 0 1 : y yMP y y x xx x    ,令 0y  , 解之得  0 0 1 0 0 1 y x xx x y y     0 0 0 1 1 0 0 0 1 0 0 1 0 1 0 1 x y x y x y x y x y x y y y y y      , ∴ 1 0 0 1 0 1 x y x ym y y   ;又因为则 0 1 0 1 NP y yk x x   ,直线  0 1 0 0 0 1 : y yNP y y x xx x    , 令 0y  可得  0 0 1 0 0 1 y x xx x y y     0 0 0 1 0 0 1 0 0 1 1 0 0 1 0 1 x y x y x y x y x y x y y y y y      , ∴ 0 1 1 0 0 1 x y x yn y y   , 1 0 0 1 0 1 1 0 0 1 0 1 x y x y x y x ymn y y y y      2 2 2 2 1 0 0 1 2 2 0 1 x y x y y y   , 由于 2 2 1 12x y  , 2 2 0 02x y  , 故    2 2 2 2 1 0 0 1 2 2 0 1 2 2y y y y mn y y      2 2 2 2 2 2 0 1 0 1 0 1 2 2 0 1 2 2y y y y y y y y     2 2 0 1 2 2 0 1 2 2 2y y y y   , ∴ mm 为定值 2 . 解析： 19.答案：1.∵圆 N 的圆心 5 5,3 3N     关于直线 y x 的对称点为 5 5,3 3M     , ∴ 2 22 4 16 3 9r MD        . ∴圆 M 的方程为 2 25 5 16 3 3 9x y             , ∵ 2 210 10 10 2 823 3 3 3MN r              已知圆 M与圆 N 相离. 2.设  0 0,P x y ,则   2 2 2 0 0 51 3PA x y         2 2 0 0 0 16 5 419 3 3x x x          ,   2 2 2 0 0 51 3PB x y         2 2 0 0 0 16 5 1619 3 3x x x          , 2 2 4PB PA  , 2PB PA  ,∵G 为 APB 的角平分线上一点, ∴ G 到 PA 与 PB 的距离相等,∴ 2PBG PAG PBS S PA     为定值. 解析： 20.答案：1.圆 2 2: 2 4 3 0C x y x y     的标准方程为 2 2( 1) ( 2) 2x y    所以圆心 ( 1,2)C  ,半径 2r  设圆的切线在 x 轴和 y 轴上的截距分别为 ,a b 当 0a b  时, 切线方程可设为 ,y kx 由点到直线的距离公式得: 2 2 1 22 1 1 a    解得: 1a   或 3a  所以切线方程为: 1 0, 3 0.x y x y      总之,所求方程为 (2 6) , 1 0y x x y     或 3 0x y    2.连接 MC ,则 2 2 2| | | |PM PC MC  因为: PC PO 所以 2 2 2| | | |PC MC PO  即: 2 2 2 2( 1) ( 2) 2x y x y      整理得: 32 2x y  2 2PM PO x y   2 2 23 9(2 ) 5 62 4y y y y      当 6 3 10 5y   时, PM 最小 此时: 3 3 32 5 2 10x     所以 3 3( , )10 5P  解析： 21.答案：1.由中点坐标公式,得 0 0 6 2 2 xx yy     即 0 2 6x x  , 0 2y y . ∵点  0 0,M x y 在圆 2 2 4x y  上运动, ∴ 2 2 0 0 4x y  ,即   2 22 6 2 4x y   ,整理,得 2 23 1x y   . ∴点 P 的轨迹C 的方程为  2 23 1x y   . 2.设  1 1,E x y ,  2 2,F x y ,直线l 的方程是 1y kx  ,代入圆 2 23 1x y   . 可得   2 21 2 3 9 0k x k x     ,由 232 24 0k k     ,得 3 04 k   , 且   1 2 2 2 3 1 kx x k    , 1 2 2 9 1x x k   , ∴     2 1 2 1 2 1 2 1 21 1 1y y kx kx k x x k x x        2 2 2 2 2 2 39 8 6 111 1 1 k kk k k k k k         ∴ 2 1 2 1 2 2 8 6 10 121 k kOE OF x x y y k         . 解得 1 2k  或1,不满足 0  . ∴不存在实数 k 使得 12OE OF   . 解析： 22.答案：1.由题得 1 2l l ,所以 ABD 是直角三角形,且  0,2 2A m ,  2 2 ,0  B m ,  2,2  D , 则 ABD 外接圆直径是 AB ,  2 28 1AB m  . 要使圆 C 的面积最小,则 2 min 8AB  ,当且仅当 0m  时成立, 所以圆 C 面积的最小值为 2 . 2.由  2,2  D 点在抛物线 2 2x py 上,得 2 2x y . 由1知圆 C 过原点,则抛物线与圆 C 的公共点是  2,2  D ,  0,0E , 假设存在点  0 0,P x y 满足条件,则 2 0 02x y . ①当 DE 是底时, DE 的中点为  1 ,1  Q , DE 的中垂线方程为 2y x   , 代入抛物线 2 2x y ,得 2 2 4 0x x   , 20  0   , 所以存在两个满足条件的 P 点. ②当 PE 是底时, PE 中点为 0 0,2 2 x yM      ,则 DM PE , 即 0 0 0 02 2 02 2 x yx y             , 3 0 04 16 0x x   . 设   3 4 16f x x x   ,   2' 3 4f x x  , 则  f x 在 2 3, 3       , 2 3,3      上递增,在 2 3 2 3,3 3      上递减. 因为 2 3 03f       ,  0 16 0f    ,  3 1 0f    ,  4 32 0f   , 所以  f x 在  3,4 内有唯一零点,存在一个满足条件的 P 点. ③当 PD 是底时, PD 中点为 0 01, 12 2 x yN      ,则 EN PD , 0 01, 12 2 x yEN        ,  0 02, 2DP x y   , 0EN DP   , 即    0 0 0 0 2 22 2 02 2 x yx y              , 所以 2 2 2 0 0 04 4 4 02 4 2 x x x          ,即   2 2 0 04 8 08 x x   , 则 2 0 4 0x   或 2 0 8 0x   , 此时只有一个解 0 2x  . 综上所述,以上零点不重复,所以共有4个满足条件的 P 点. 解析：