- 2021-04-18 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
吉林省四平四中2018-2019学年下学期高二期中考试+文科数学-+Word版含答案(范围:选修1-2、4-4)
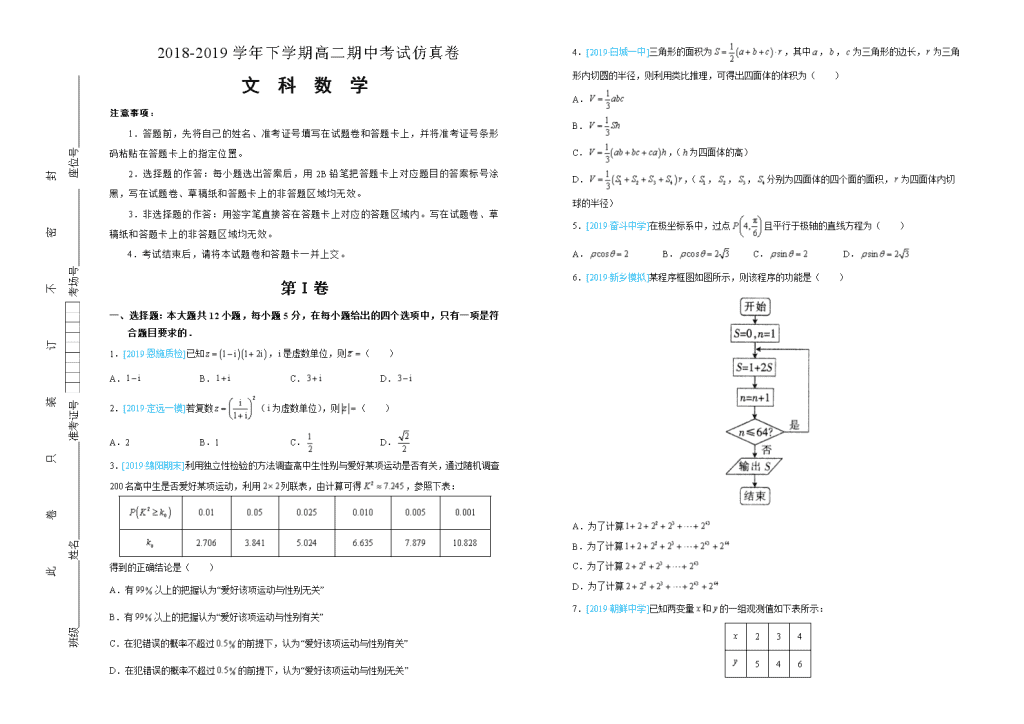
此卷只装订不密封 班级 姓名 准考证号 考场号 座位号 2018-2019学年下学期高二期中考试仿真卷 文科数学 注意事项: 1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。 2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。 3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。 4.考试结束后,请将本试题卷和答题卡一并上交。 第Ⅰ卷 一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.[2019·恩施质检]已知,是虚数单位,则( ) A. B. C. D. 2.[2019·定远一模]若复数(为虚数单位),则( ) A.2 B.1 C. D. 3.[2019·绵阳期末]利用独立性检验的方法调查高中生性别与爱好某项运动是否有关,通过随机调查200名高中生是否爱好某项运动,利用列联表,由计算可得,参照下表: 得到的正确结论是( ) A.有以上的把握认为“爱好该项运动与性别无关” B.有以上的把握认为“爱好该项运动与性别有关” C.在犯错误的概率不超过的前提下,认为“爱好该项运动与性别有关” D.在犯错误的概率不超过的前提下,认为“爱好该项运动与性别无关” 4.[2019·白城一中]三角形的面积为,其中,,为三角形的边长,为三角形内切圆的半径,则利用类比推理,可得出四面体的体积为( ) A. B. C.,(为四面体的高) D.,(,,,分别为四面体的四个面的面积,为四面体内切球的半径) 5.[2019·奋斗中学]在极坐标系中,过点且平行于极轴的直线方程为( ) A. B. C. D. 6.[2019·新乡模拟]某程序框图如图所示,则该程序的功能是( ) A.为了计算 B.为了计算 C.为了计算 D.为了计算 7.[2019·朝鲜中学]已知两变量和的一组观测值如下表所示: 2 3 4 5 4 6 如果两变量线性相关,且线性回归方程为,则( ) A. B. C. D. 8.[2019·济南外国语]甲、乙、丙、丁四位同学参加一次数学智力竞赛,决出了第一名到第四名的四个名次.甲说:“我不是第一名”;乙说:“丁是第一名”;丙说:“乙是第一名”;丁说:“我不是第一名”.成绩公布后,发现这四位同学中只有一位说的是正确的,则获得第一名的同学为( ) A.甲 B.乙 C.丙 D.丁 9.[2019·武邑中学]已知直线的参数方程为 (为参数),则直线的倾斜角为( ) A. B. C. D. 10.[2019·三明期末]执行如图的程序框图,如果输出的,那么判断框内可填入的条件是( ) A. B. C. D. 11.[2019·抚顺期末] “杨辉三角”又称“贾宪三角”,是因为贾宪约在公元1050年首先使用“贾宪三角”进行高次开方运算,而杨辉在公元1261年所著的《详解九章算法》一书中,记录了贾宪三角形数表,并称之为“开方作法本源”图.下列数表的构造思路就源于“杨辉三角”.该表由若干行数字组成,从第二行起,每一行中的数字均等于其“肩上”两数之和,表中最后一行仅有一个数,则这个数是( ) 2017 2016 2015 2014……6 5 4 3 2 1 4033 4031 4029…………11 9 7 5 3 8064 8060………………20 16 12 8 16124……………………36 28 20 ……………………… A. B. C. D. 12.[2019·哈三中]已知椭圆的离心率,为椭圆上的一个动点,则与定点连线距离的最大值为( ) A. B. C. D. 第Ⅱ卷 二、填空题:本大题共4小题,每小题5分. 13.[2019·伊春二中] _______. 14.[2019·衡阳一中]将正整数有规律地排列如下: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 …………… 则在此表中第45行第83列出现的数字是_______________ 15.[2019·朝鲜中学]某医疗研究所为了检验某种血清对预防感冒的作用,把500名使用该血清的人与另外500名未使用血清的人一年中的感冒记录作比较,提出假设:这种血清不能起到预防感冒的作用.利用列联表计算得,经查临界值表知.给出下列三种说法: ①有的把握认为“这种血清能起到预防感冒的作用”; ②如果某人未使用该血清,那么他在一年中有的可能性得感冒; ③这种血清预防感冒的有效率为. 则上述说法中,正确说法的序号是________. 16.[2019·复旦附中]设、分别为直线(为参数,)和曲线(为参数,)上的点,则的取值范围是______. 三、解答题:本大题共6大题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.(10分)[2019·南京期末]已知复数,复数,其中是虚数单位,,为实数. (1)若,为纯虚数,求的值; (2)若,求,的值. 18.(12分)[2019·沧州期末]为保护农民种粮收益,促进粮食生产,确保国家粮食安全,调动广大农民粮食生产的积极性,从2004年开始,国家实施了对种粮农民直接补贴.通过对2014~2018年的数据进行调查,发现某地区发放粮食补贴额(亿元)与该地区粮食产量(万亿吨)之间存在着线性相关关系.统计数据如下表: 年份 2014年 2015年 2016年 2017年 2018年 补贴额亿元 9 10 12 11 8 粮食产量万亿吨 23 25 30 26 21 (1)请根据如表所给的数据,求出关于的线性回归直线方程; (2)通过对该地区粮食产量的分析研究,计划2019年在该地区发放粮食补贴额7亿元,请根据(1)中所得的线性回归直线方程,预测2019年该地区的粮食产量. (参考公式:,) 19.(12分)[2019·驻马店期末]某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本,并称出它们的重量(单位:克),重量值落在内的产品为合格品,否则为不合格品. 注:表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图. 产品重量(克) 频数 6 8 14 8 4 (1)根据上面表1中的数据在图2中作出甲流水线样本的频率分布直方图; (2)若以频率作为概率,试估计从两条流水线上分别任取1件产品,该产品恰好是合格品的概率分别是多少; (3)由以上统计数据完成下面列联表,并回答有多大的把握认为产品的包装质量与两条自动包装流水线的选择有关. 甲流水线 乙流水线 合计 合格 不合格 合计 参考公式:,其中 20.(12分)[2019·都匀一中]某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数。 ①; ②; ③; ④; ⑤. (1)试从上述五个式子中选择一个,求出这个常数; (2)根据(1)的计算结果,将该同学的发现推广为三角恒等式,并证明你的结论. 21.(12分)[2019·新乡二模]在直角坐标系中,曲线的参数方程为(为参数).以坐标原点为极点,轴正半轴为极轴建立极坐标系,直线的极坐标方程为. (1)求和的直角坐标方程; (2)已知直线与轴交于点,且与曲线交于,两点,求的值. 22.(12分)[2019·莆田质检]在直角坐标系中,直线的参数方程为(为参数),以坐标原点为极点,轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为. (1)求的极坐标方程和的直角坐标方程; (2)若曲线的极坐标方程为,与的交点为,与异于极点的交点为,求. 2018-2019学年下学期高二期中考试仿真卷 文科数学答案 第Ⅰ卷 一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.【答案】D 【解析】由,∴,故选D. 2.【答案】C 【解析】复数,根据模长的公式得到.故选C. 3.【答案】B 【解析】由,可得有以上的把握认为“爱好该项运动与性别有关”.故选B. 4.【答案】D 【解析】设四面体的内切球的球心为,则球心到四个面的距离都是, 根据三角形的面积的求解方法:分割法,将与四顶点连起来,可得四面体的体积等于以为顶点,分别以四个面为底面的4个三棱锥体积的和, ∴,故选D. 5.【答案】C 【解析】∵将点的极坐标化成直角坐标为,∴此点到轴的距离为2, ∴经过此点到轴的距离为2的直线的方程是, ∴过点且平行于极轴的直线的方程是,故选C. 6.【答案】A 【解析】运行程序,,,,,判断是;,, 判断是,,,, 以此类推,表达式的最后一项的指数比下一个要少, 故,,退出程序,输出的值. ∴程序框图是为了计算,故选A. 7.【答案】D 【解析】,,代入线性回归方程可得, 解之得.故选D. 8.【答案】A 【解析】当甲获得第一名时,甲、乙、丙说的都是错的,丁说的是对的,符合条件; 当乙获得第一名时,甲、丙、丁说的都是对的,乙说的是错的,不符合条件; 当丙获得第一名时,甲和丁说的是对的,乙和丙说的是错的,不符合条件; 当丁获得第一名时,甲、乙说的都是对的,乙、丁说的都是错的,不符合条件. 故选A. 9.【答案】A 【解析】∵,∴, 故直线的斜率为,倾斜角为,故选A. 10.【答案】C 【解析】进入循环前,,, 计算,应满足循环条件,; 执行循环后,应满足循环条件,; 执行循环后,应满足循环条件,; 执行循环后,应不满足循环条件,输出; 故判断框内应填入的条件是,故选C. 11.【答案】B 【解析】由题意,数表的每一行都是等差数列,从右到左, 且第一行公差为1,第二行公差为2,第三行公差为4,,第2015行公差为, 故第1行的第一个数为:, 第2行的第一个数为:, 第3行的第一个数为:, 第行的第一个数为:, 第2017行只有,则.故选B. 12.【答案】C 【解析】椭圆的离心率,可得,解得, 椭圆方程为,设, 则与定点连线距离为 . 当时,取得最大值,故选C. 第Ⅱ卷 二、填空题:本大题共4小题,每小题5分. 13.【答案】 【解析】. 14.【答案】2019 【解析】依题意可知第行有个数字, 前行的数字个数为个,可得前44行共个, ∵,即第44行最后一个数为1936, ∴第45行第83列出现的数字是,故答案为2019. 15.【答案】① 【解析】根据已知能判断有的把握认为“这种血清能起到预防感冒的作用”, ∴选项①是正确的; 如果某人未使用该血清,不能说明他在一年中有的可能性得感冒, ∴选项②是错误的; 这种血清预防感冒的有效率为95%,不是.∴选项③是错误的.故答案为①. 16.【答案】 【解析】由(为参数)可得直线的普通方程为, 由(为参数)可得曲线的普通方程为, ∵点、分别为直线和圆上的动点, ∴,可以无穷远, ∴的取值范围是,故答案是. 三、解答题:本大题共6大题,共70分.解答应写出文字说明、证明过程或演算步骤. 17.【答案】(1);(2),. 【解析】(1)∵为纯虚数,∴, 又,∴,,从而, 因此. (2)∵,∴,即, 又,为实数,∴,解得. 18.【答案】(1)(2)粮食产量大约为万亿吨. 【解析】(1)由已知数据,可得,. 代入公式,经计算,得, ∴.∴所求关于的线性回归直线方程为. (2)由题意,知,代入(1)中所得线性回归直线方程,计算得. ∴2019年该地区的粮食产量大约为万亿吨. 19.【答案】(1)见解析;(2)从甲流水线上任取1件产品,该产品恰好是合格品的概率为;从乙流水线上任取1件产品,该产品恰好是合格品的概率为;(3)见解析. 【解析】(1)甲流水线样本的频率分布直方图如下: (2)由表1知甲流水线样本中合格品数为, 故甲流水线样本中合格品的频率为, 由图1知乙流水线样本中合格品的频率为, 据此可估计从甲流水线上任取1件产品,该产品恰好是合格品的概率为; 从乙流水线上任取1件产品,该产品恰好是合格品的概率为. (3)由(2)知甲流水线样本中合格品数为30,乙流水线样本中合格品数为. 列联表如下: 甲流水线 乙流水线 合计 合格 30 36 66 不合格 10 4 14 合计 40 40 80 ∵, ∴有的把握认为产品的包装质量与两条自动包装流水线的选择有关. 20.【答案】(1);(2),证明见解析. 【解析】(1); (2)三角恒等式为:, . 21.【答案】(1)直线的直角坐标方程为,的普通方程;(2). 【解析】(1)∵直线的极坐标方程为, ∴直线的直角坐标方程为, ∵曲线的参数方程为(为参数),∴曲线的普通方程. (2)由题可知, ∴直线的参数方程为,(为参数),代入,得. 设,两点所对应的参数分别为,,则,. ∴. 22.【答案】(1),;(2). 【解析】(1)∵直线的参数方程为(为参数), ∴直线的普通方程为, 又,,故直线的极坐标方程为. 由曲线的极坐标方程为,得, ∴曲线的直角坐标方程为. (2),,则,解得. 又,∴.查看更多