高考数学平面向量题的七种解法

高考数学平面向量题的七种解法

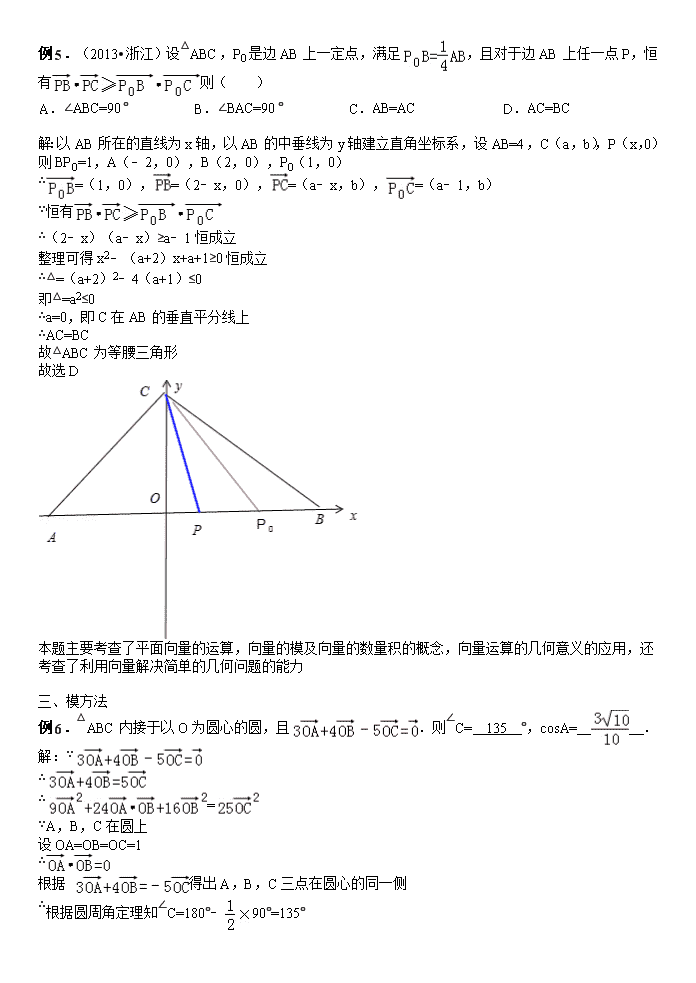
高考数学平面向量题的七种解法 玉林高中 刘飞 一、 基底法 例1．(2013·江苏) 设D，E分别是△ABC的边AB，BC上的点，AD＝AB，BE＝BC.若＝λ1＋λ2(λ1，λ2为实数)，则λ1＋λ2的值为________．‎ ‎【答案】　‎ ‎[解析] 如图所示，＝－＝－＝(－)＋＝＋，‎ 又＝λ1＋λ2，且与不共线，所以λ1＝－，λ2＝，‎ 即λ1＋λ2＝.‎ 例2．(2013·天津) 在平行四边形ABCD中，AD＝1，∠BAD＝60°，E为CD的中点，若·＝1，则AB的长为________．‎ ‎【答案】　 www.21cnjy.com ‎[解析] 由题意得＝－＝＋－＝－，＝＋，所以·＝(＋)＝2－2＋·＝1－2＋||×1×＝1，解得||＝或0(舍去)．‎ 例3.（2007•天津）如图，在中，，是边上一点，，则　　　　　．‎ 法一：选定基向量，，由图及题意得，=‎ ‎∴=（）（）=+==‎ 法二：由题意可得 ‎∴，‎ ‎∵，‎ ‎∴=．‎ 故答案为：﹣．‎ 一、 坐标法 例4．（2013•重庆）在平面上，，=1，．若||＜，则||的取值范围是（　　）‎ ‎　‎ A．‎ ‎（0，]‎ B．‎ ‎（，]‎ C．‎ ‎（，]‎ D．‎ ‎（，]‎ 解：根据条件知A，B1，P，B2构成一个矩形A，B1PB2，以AB1，AB2所在直线为坐标轴建立直角坐标系，设|AB1|=a，|AB2|=b，点O的坐标为（x，y），则点P的坐标为（a，b），‎ 由=1，得，则 ‎∵||＜，∴‎ ‎∴‎ ‎∴‎ ‎∵（x﹣a）2+y2=1，∴x2+y2+a2=1+2ax≤1+a2+x2，∴y2≤1‎ 同理x2≤1‎ ‎∴x2+y2≤2②‎ 由①②知，‎ ‎∵||=，∴＜||≤‎ 故选D．‎ 例5．（2013•浙江）设△ABC，P0是边AB上一定点，满足，且对于边AB上任一点P，恒有则（　　）‎ ‎　‎ A．‎ ‎∠ABC=90°‎ B．‎ ‎∠BAC=90°‎ C．‎ AB=AC D．‎ AC=BC 解：以AB所在的直线为x轴，以AB的中垂线为y轴建立直角坐标系，设AB=4，C（a，b），P（x，0）‎ 则BP0=1，A（﹣2，0），B（2，0），P0（1，0）‎ ‎∴=（1，0），=（2﹣x，0），=（a﹣x，b），=（a﹣1，b）‎ ‎∵恒有 ‎∴（2﹣x）（a﹣x）≥a﹣1恒成立 整理可得x2﹣（a+2）x+a+1≥0恒成立 ‎∴△=（a+2）2﹣4（a+1）≤0‎ 即△=a2≤0‎ ‎∴a=0，即C在AB的垂直平分线上 ‎∴AC=BC 故△ABC为等腰三角形 故选D 本题主要考查了平面向量的运算，向量的模及向量的数量积的概念，向量运算的几何意义的应用，还考查了利用向量解决简单的几何问题的能力 一、 模方法 例6．△ABC内接于以O为圆心的圆，且．则∠C=　135　°，cosA=　　．‎ 解：∵‎ ‎∴‎ ‎∴=‎ ‎∵A，B，C在圆上 设OA=OB=OC=1‎ ‎∴‎ 根据 得出A，B，C三点在圆心的同一侧 ‎∴根据圆周角定理知∠C=180°﹣90°=135°‎ 同理求出=，‎ cos∠BOC=‎ ‎∵∠A是∠BOC的一半 ‎∴‎ 故答案为：135°；‎ 例7．（2013•浙江）设、为单位向量，非零向量=x+y，x、y∈R．若、的夹角为30°，则的最大值等于　2　．‎ 解：∵、 为单位向量，和的夹角等于30°，∴=1×1×cos30°=．‎ ‎∵非零向量=x+y，∴||===，‎ ‎∴====，‎ 故当=﹣时，取得最大值为2，‎ 故答案为 2．‎ 一、 数量积法 例8．给定两个长度为1的平面向量和，它们的夹角为.‎ 如图所示，点C在以O为圆心的圆弧上变动.‎ 若其中,则 的最大值是________.‎ ‎[解析]设 ‎ ‎，即 ‎∴‎ 例9．在△ABC中，AB=2AC=2，∠BAC=120°，，若 ‎（O是△ABC的外心），则x1+x2的值为　　．‎ 解答：‎ 解：如图：以A为原点，以AB所在的直线为x轴，建立直角系：则A（0，0），B （2，0），C（﹣，）．‎ ‎∵O为△ABC的外心，∴O在AB的中垂线 m：x=1 上，又在AC的中垂线 n 上，‎ AC的中点（﹣，），AC的斜率为﹣3，∴中垂线n的方程为 y﹣=（x+）．‎ 把直线 m和n 的方程联立方程组解得△ABC的外心O（1，），由条件 =，‎ 得（1， ）=x1 （2，0）+x2 （﹣，）=（2x1﹣x2， x2 ），‎ ‎∴2x1﹣x2=1， x2=，∴x1 =，x2 =，∴x1+x2=，‎ 故答案为：．‎ 点评：‎ 本题考查求两条直线的交点坐标的方法，三角形外心的性质，向量的坐标表示及向量相等的条件，待定系数法求参数值．属中档题．‎ 一、 几何法 例10．在△ABC中，若对任意k∈R，有|﹣k|≥||，则△ABC的形状是（　　）‎ ‎　‎ A．‎ 直角三角形 B．‎ 等腰三角形 ‎　‎ C．‎ 等腰三角形或直角三角形 D．‎ 等腰直角三角形 解：如图：设 =k，则 ﹣k =，不等式即||≥||，‎ ‎∴||是点A与直线BC上的点连线得到的线段中，长度最小的一条，故有AC⊥BC，‎ 故则△ABC为 直角三角形，‎ 故选A．‎ 本题考查向量和、差的模的几何意义，体现了等价转化的数学思想，把题中条件转化为AC⊥BC．‎ 例11．（2013•湖南）已知，是单位向量，，若向量满足，则的取值范围为（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 解：令，，，‎ 如图所示：则，‎ 又，所以点C在以点D为圆心、半径为1的圆上，‎ 易知点C与O、D共线时达到最值，最大值为+1，最小值为﹣1，‎ 所以的取值范围为[﹣1，+1]．‎ 故选A．‎ 例12．图3‎ 2005年全国（I）卷第15题“的外接圆的圆心为，两条边上的高的交点为，，则实数=________”‎ 先解决该题：‎ 作直经，连，,有，，，，，故，‎ 故是平行四边形，进而，又 ‎∴‎ 故，所以 评注：外心的向量表示可以完善为：‎ 若为的外心，为垂心，则。其逆命题也成立。‎ 一、 面积法 结论：. O为△ABC内一点，记，求证： ‎ 证明：如图4建立坐标系。‎ 设 则，‎ 从而 由于故 所以 例13．（2007•南通模拟）已知O是△ABC内一点，，则△AOB与△AOC的面积的比值为　　．‎ 解：设M为AC的中点，则由向量加法的平行四边形法则可得 由可得，从而可得B，O，M三点共线 即BM为AC边上的中线 由2OM=3BO可得，‎ ‎∴S△AOB=S△COB=‎ ‎∴‎ 故答案为：‎ 本题主要考查了平面向量的加法的平行四边形的应用，向量的共线与点共线的相互转化，解题的关键是要发现由2OM=3BO可得，及三角形AOB与三角形BOC的面积相等 一、 射影法 例14．已知P为△ABC的外心，且||=4，||=2，则•等于　6　．‎ 解：•＝•（﹣）‎ 作PD⊥AC于D，则 ‎∵P为△ABC的外心，∴=，‎ 可得•=||•||cos∠PAD=||•||=||2=8‎ 同理可得•=||2=2‎ ‎∴•（﹣）=•﹣•=8﹣2=6‎ 故答案为：6‎ 本题在三角形中给出外心，求向量数量积的式子．着重考查了三角形的外心的性质、向量数量积的定义与运算性质等知识，属于中档题．‎ 例15.（2013•绵阳模拟）已知O为△ABC的外心，的最大值为（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ 法一、‎ 法二、‎ 解：如图所示，以BC边所在直线为x轴，BC边的垂直平分线为y轴建立直角坐标系 ‎（D为BC边的中点）．‎ 由外接圆的性质可得∠BOD=∠COD=∠BAC．‎ 由，不妨设外接圆的半径R=3．则OA=OB=OC=3．‎ ‎∵，∴OD=1.．‎ ‎∴B，C，O（0，1），A（m，n）．‎ 则△ABC外接圆的方程为：x2+（y﹣1）2=9．（*）‎ ‎∵，‎ ‎∴（﹣m，1﹣n）=，‎ ‎∴，‎ ‎∵α+β≠1时，否则，由图可知是不可能的．‎ ‎∴可化为，代入（*）可得，‎ 化为18（α+β）=9+32αβ，‎ 利用重要不等式可得，‎ 化为8（α+β）2﹣18（α+β）+9≥0，‎ 解得或．‎ 又α+β＜1，故应舍去．‎ ‎∴，‎ 故α+β的最大值为．‎ 故选D．‎ 点评：‎ 本题考查了通过建立直角坐标系解决向量的有关运算、圆的标准方程、基本不等式的性质、‎ 一元二次不等式的解法、三角形的外接圆的性质、余弦函数等基础知识与基本技能方法，‎ 属于难题．‎