- 2021-04-18 发布 |
- 37.5 KB |
- 33页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
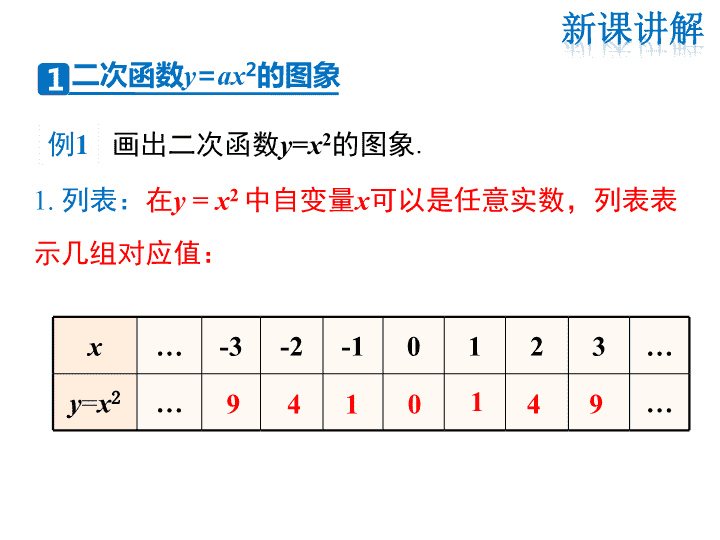
华师版数学九年级下册课件-第26章 二次函数-26二次函数的图象与性质
HS九(下) 教学课件 第26章 二次函数 1. 二次函数y=ax2的图象与性质 26.2 二次函数的图象与性质 二次函数y=ax2的图象 x … -3 -2 -1 0 1 2 3 … y=x2 … … 画出二次函数y=x2的图象. 9 4 1 0 1 94 1. 列表:在y = x2 中自变量x可以是任意实数,列表表 示几组对应值: 1 例1 2 4-2-4 o 3 6 9 x y 2. 描点:根据表中x, y的数值在坐标平面中描点(x,y) 3. 连线:如图,再用平滑曲线顺次连接各点,就得到 y = x2 的图象. -3 3o 3 6 9 当取更多个点时,函数y=x2的图象如下. x y 二次函数y=x2的图象形如物体抛射时所经过的 路线,我们把它叫做抛物线. 这条抛物线关于y轴对称, y轴就是它的对称轴. 对称轴与抛物线的交 点叫做抛物线的顶点. 练一练:画出函数y=-x2的图象. y 2 4-2-4 0 -3 -6 -9 x x … -3 -2 -1 0 1 2 3 … y=-x2 … -9 -4 -1 0 -1 -4 -9 … 根据你以往学习函数图象性质的经验,说说二次 函数y=x2的图象有哪些性质,并与同伴交流. xo y=x2 1.y=x2是一条抛物线; 2.图象开口向上; 3.图象关于y轴对称; 4.顶点( 0 ,0 ); 5.图象有最低点. y 说说二次函数y=-x2的图象有哪些性质,与同伴交流. o x y y=-x2 1.y=-x2是一条抛物线; 2.图象开口向下; 3.图象关于y轴对称; 4.顶点( 0 ,0 ); 5.图象有最高点. 1. 顶点都在原点; 3.当a>0时,开口向上; 当a<0时,开口向下. 二次函数y=ax2 的图象性质: 2. 图像关于y轴对称; 知识要点 观察下列图象,抛物线y=ax2与y=-ax2(a>0)的 关系是什么? 二次项系数互为相反数, 开口相反,大小相同, 它们关于x轴对称. x y O y=ax2 y=-ax2 交流讨论 二次函数y=ax2的性质 问题1:观察图形,y随x的变化如何变化? (-2,4) (-1,1) (2,4) (1,1) 2y x 2y ax 2 对于抛物线 y = ax 2 (a>0) 当x>0时,y随x取值的增大而增大; 当x<0时,y随x取值的增大而减小. 知识要点 (-2,-4) (-1,-1) (2,-4) (1,-1) 2y x 2y ax 问题2:观察图形,y随x的变化如何变化? 对于抛物线 y = ax 2 (a<0) 当x>0时,y随x取值的增大而减小; 当x<0时,y随x取值的增大而增大. 知识要点 解:分别填表,再画出它们的图象,如图. x ··· -4 -3 -2 -1 0 1 2 3 4 ··· ··· ··· x ··· - 2 -1.5 - 1 -0.5 0 0.5 1 1.5 2 ··· ··· ··· 21 2y x 22y x 8 4.5 2 0.5 0 84.520.5 8 4.5 2 0.5 0 84.520.5 在同一直角坐标系中,画出函数 的 图象. 2 21 22 ,y x y x例2 -2 2 2 4 6 4-4 8 21 2y x 22y x2y x 思考1:从二次函数 开口大小 与a的大小有什么关系? 2 2 21 , , 22y x y x y x 当a>0时,a越大,开口越小. 练一练:在同一直角坐标系中,画出函数 的图象. 2 21 22 ,y x y x x ··· -4 -3 -2 -1 0 1 2 3 4 ··· ··· ··· x ··· -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 ··· ··· ··· -8 -4.5 -2 -0.5 0 -8 -4.5 -2 -0.5 -8 -4.5 -2 -0.5 0 -8-4.5-2-0.522y x 21 2y x -2 2 -2 -4 -6 4-4 -8 21 2 y x 22y x 2y x 当a<0时,a越小(即 a的绝对值越大), 开口越小. 思考2:从二次函数 开口大 小与a的大小有什么关系? 2 2 21 22 , ,y x y x y x 对于抛物线 y = ax 2 ,|a|越大,抛物线的开口越小. y=ax2 a>0 a<0 图象 位置开 口方向 对称性 顶点最值 增减性 开口向上,在x轴上方 开口向下,在x轴下方 a的绝对值越大,开口越小 关于y轴对称,对称轴是直线x=0 顶点坐标是原点(0,0) 当x=0时,y最小值=0 当x=0时,y最大值=0 在对称轴左侧递减 在对称轴右侧递增 在对称轴左侧递增 在对称轴右侧递减 y O x y O x 已知二次函数y=x2. (1)判断点A(2,4)在二次函数图象上吗? (2)请分别写出点A关于x轴的对称点B的坐标,关 于y轴的对称点C的坐标,关于原点O的对称点 D的坐标; (3)点B、C、D在二次函数y=x2的图象上吗?在二 次函数y=-x2的图象上吗? 例3 (1)判断点A(2,4)在二次函数图象上吗? 解:当x=2时,y=x2=4, 所以A(2,4)在二次函数图象上. (2)请分别写出点A关于x轴的对称点B的坐标,关于y 轴的对称点C的坐标,关于原点O的对称点D的坐 标; 解:点A关于x轴的对称点B的坐标为(2,-4), 点A关于y轴的对称点C的坐标为(-2,4), 点A关于原点O的对称点D的坐标为(-2,-4). (3)点B、C、D在二次函数y=x2的图象上吗?在二次函 数y=-x2的图象上吗? 解:当x=-2时,y=x2=4, 所以C点在二次函数y=x2的图象上; 当x=2时,y=-x2=-4, 所以B点在二次函数y=-x2的图象上; 当x=-2时,y=-x2=-4, 所以D点在二次函数y=-x2的图象上. 已知 是二次函数,且当x>0时, y随x增大而增大,则k= . 2 42( ) k ky k x 分析: 是二次函数,即二次项的系数 不为0,x的指数等于2.又因当x>0时,y随x增大而增大, 即说明二次项的系数大于0.因此, 2 42 ( ) k ky k x 2 4 2 2 0 k k k > 解得 k=2 2 已知二次函数y=2x2. (1)若点(-2,y1)与(3,y2)在此二次函数的图象上,则 y1_____y2;(填“>”“=”或“<”); (2)如图,此二次函数的图象经过点(0,0),长方形 ABCD的顶点A、B在x轴上,C、D恰好在二次函数 的图象上,B点的横坐标为2,求图中阴影部分的面 积之和. < 例4 分析:(1)把两点的横坐标代入二次函数表达式求 出纵坐标,再比较大小即可得解; (2)由于函数图象经过点B,根据点B的横坐标为2, 代入表达式可求出点C的纵坐标,再根据二次函 数图象关于y轴对称求出OA=OB,即图象左边部 分与右边部分对称,两个阴影部分面积相加等于 右边第一象限内的矩形面积. (2)解:∵二次函数y=2x2的图象经过点B, ∴当x=2时,y=2×22=8. ∵抛物线和长方形都是轴对称图形, 且y轴为它们的对称轴, ∴OA=OB, ∴在长方形ABCD内, 左边阴影部分面积等于右边空白部分面积, ∴S阴影部分面积之和=2×8=16. 方法总结:二次函数y=ax2的图象关于y轴对 称,因此左右两部分折叠可以重合,在二次函数 比较大小中,我们根据图象中点具有的对称性转 变到同一变化区域中(全部为升或全部为降),根 据图象中函数值高低去比较;对于求不规则的图 形面积,采用等面积割补法,将不规则图形转化 为规则图形以方便求解. 1.函数y=2x2的图象的开口 , 对称轴 ,顶点是 ; 在对称轴的左侧,y随x的增大而 , 在对称轴的右侧, y随x的增大而 . 2.函数y=-3x2的图象的开口 , 对称轴 ,顶点是 ; 在对称轴的左侧, y随x的增大而 , 在对称轴的右侧, y随x的增大而 . 向上 向下 y轴 y轴 (0,0) (0,0) 减小 减小 增大 增大 x x y y O O 3、如右图,观察函数y=( k-1)x2 的图象,则k的取值范围是 . x y k>1 4、说出下列抛物线的开口方向、对称轴 和顶点: 23xy 23xy 2 3 1 xy 2 3 1 xy 开口方向 对称轴 顶点 向上 向下 向下 向上 y轴 y轴 y轴 y轴 (0,0) (0,0) (0,0) (0,0) O 5.若抛物线y=ax2 (a ≠ 0),过点(-1,2). (1)则a的值是 ; (2)对称轴是 ,开口 . (3)顶点坐标是 ,顶点是抛物线上的最 值 . 抛物线在x轴的 方(除顶点外). (4)若A(x1,y1),B(x2,y2)在这条抛物线上,且x1查看更多