- 2021-04-18 发布 |
- 37.5 KB |
- 2页

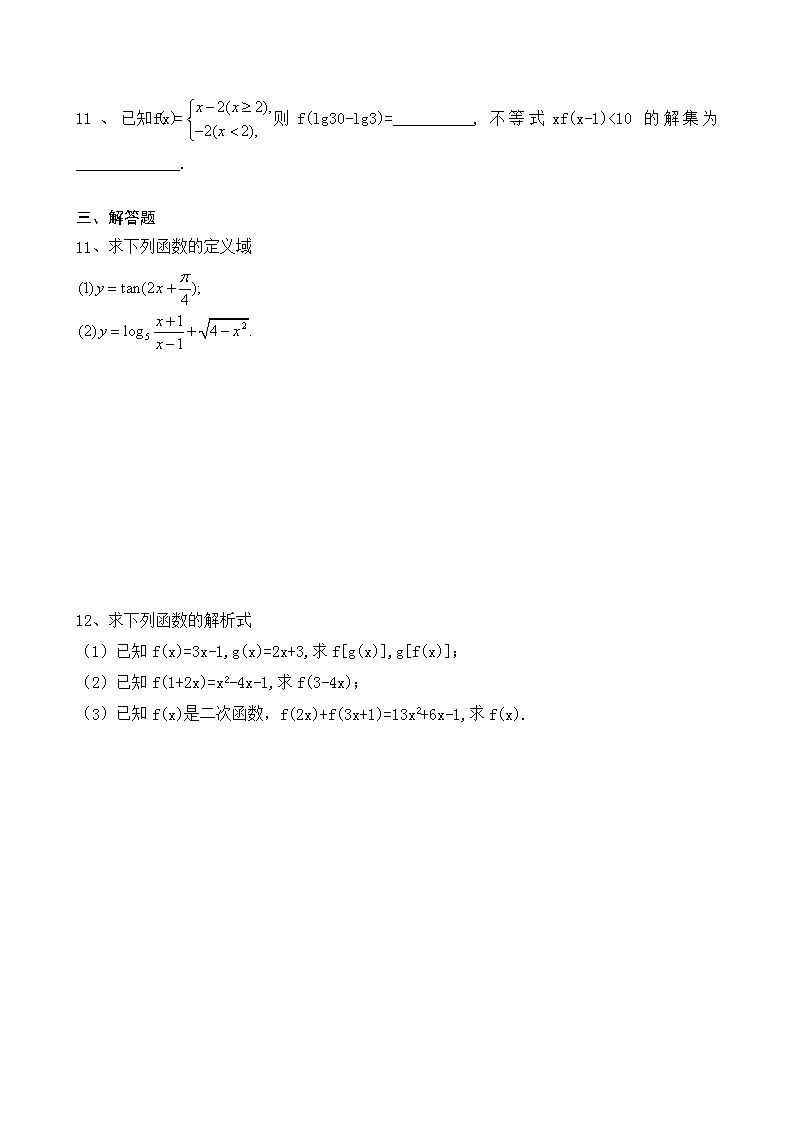
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018文科数学高考后作业函数的概念及其表示
函数的概念及其表示 一、选择题 1.下列函数为同一函数的是 ( ) A.y=x2-2x和y=t2-2t B.y=x0和y=1 C. D.y=lgx2和y=2lgx 2.函数的定义域是( ) A. B. C. D. 3.已知 ( ) A. B. C. D. 4.若二次函数g(x)满足g(1)=1,g(-1)=5,且图像过原点,则g(x)的解析式为( ) A.f(x)=|x| B.f(x)=x-|x| C.f(x)=x+1 D.f(x)=-x 5.已知函数若若f(f(0))=a,则实数a等于( ) A. B. C.2 D.9 6、已知函数f(x)的定义域为(-1,0),则函数f(2x-1)的定义域为( ) A. B. C. D. 7、若,则f(2)的值为( ) A.1 B.-1 C. D. 8、已知函数f(x)对任意实数x,y均匀f(xy)=f(x)+f(y),且f(2)=1,则f()=( ) A.1 B.-1 C. D. 二、填空题 9、则一次函数f(x)=_____________. 10、函数f(x)对任意实数x满足条件,若f(1)=-5,则f(f(5))=___________. 11、则f(lg30-lg3)=__________,不等式xf(x-1)<10的解集为_____________. 三、解答题 11、求下列函数的定义域 12、求下列函数的解析式 (1)已知f(x)=3x-1,g(x)=2x+3,求f[g(x)],g[f(x)]; (2)已知f(1+2x)=x2-4x-1,求f(3-4x); (3)已知f(x)是二次函数,f(2x)+f(3x+1)=13x2+6x-1,求f(x).查看更多