高一数学必修5课件-2等比数列第一课时

高一数学必修5课件-2等比数列第一课时

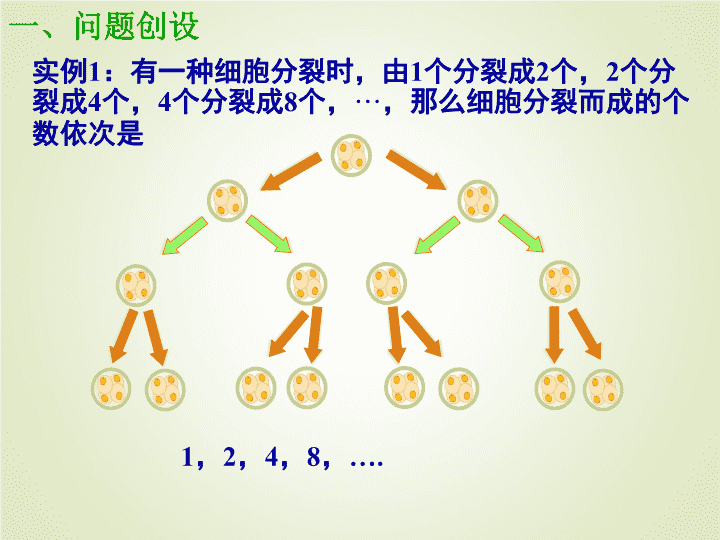
实例1：有一种细胞分裂时，由1个分裂成2个，2个分 裂成4个，4个分裂成8个，···，那么细胞分裂而成的个 数依次是 1，2，4，8，…. 一、问题创设 实例2：“一尺之棰，日取其半，万世不竭” 。如果 将“一尺之棰”视为一份，那么每日剩下的部分依次 为 一、问题创设 1 1 1 1 1 2 4 8 16 32 ， ， ， ， ， 实例3：许总年初在澄中对面的一家奶茶店投资30000 元，如果年收益率是5%，那么按照复利，5年内各年 末的本利和依次为 2 530000 1.05, 30000 1.05 , , 30000 1.05   思考：以上三个数列，每个数列相邻两项之间有什 么关系？这三个数列有什么共同的特点？ 数列①从第2项起,每一项与它前一项的比都等于____ 数列②从第2项起,每一项与它前一项的比都等于____ 数列③从第2项起,每一项与它前一项的比都等于____ 2 1.05 1 2 特点：从第二项起，每一项与它的前一项的比是同一常数 （等比） 1，2，4，8，…. 1 1 1 1 1 2 4 8 16 32 ， ， ， ， ， 2 530000 1.05, 30000 1.05 , , 30000 1.05   一、问题创设 一般地，如果一个数列从第二项起，每一项与它 的前一项的差都等于同一个常数，那么这个数列就叫 做等差数列。这个常数就叫做等差数列的公差， 公差 通常用字母 d 表示。 等差数列概念 一般地，如果一个数列从第2项起，每一项 与它的前一项的 都等于同一常数，那么这个 数列叫做 ，这个常数叫做 数列 的 ，通常用字母 表示。 比 等比数列 等比 公比 q 类 比 思考：用数学符号语言（递推公式）怎样表示 等比数列的定义呢？ 一般地，如果一个数列从第二项起，每一项与它 的前一项的比都等于同一个常数，那么这个数列就叫 做等比数列。这个常数就叫做等比数列的公比， 公比 通常用字母 q 表示。 1、等比数列的定义： 1 n n a qa   或 1n n a qa   (q≠0) ( 2)n  *( )n N 等比数列的每一 项都不为0，即 an≠0。 二、基础知识讲解 练习1：下列数列是等比数列吗？是的话，请指出 它们的公比q. 1 64,32,16,8, 2 1,-1,1,-1, 3 - 3,-9,-27,-80, 4 , , , ,a a a a     （ ） （ ） （ ） （ ） 是，q=1/2 是，q=-1 不是 不一定是 0 0 a a   时不是等比数列； 时是等比数列。 思考1：已知等比数列{ an }， (1) a1 能不能是零？ (2)公比 q 能不能是1？ 不能 能 练习1：下列数列是等比数列吗？是的话，请指出 它们的公比q. 思考2：在等比数列中，各项的符号与公比q有什么关 系？ 1 64,32,16,8, 2 1,-1,1,-1, 3 - 3,-9,-27,-80, 4 , , , ,a a a a     （ ） （ ） （ ） （ ） 若q>0，则各项的符号与a1相同； 若q<0，则各项的符号正负相间. 是，q=1/2 是，q=-1 不是 不一定是 0 0 a a   时不是等比数列； 时是等比数列。 练习1：下列数列是等比数列吗？是的话，请指出 它们的公比q. 1 64,32,16,8, 2 1,-1,1,-1, 3 - 3,-9,-27,-80, 4 , , , ,a a a a     （ ） （ ） （ ） （ ） 是，q=1/2 是，q=-1 不是 不一定是 0 0 a a   时不是等比数列； 时是等比数列。 思考3：什么样的数列既是等差数列，又是等比数列？ 非零的常数列 练习2：能否在下列两个数中间插入一个数，使这三个 数组成一个等比数列？可以的话，请求出插入的数字 (1) 12, , 0 (2) 2, , 8 (3) 3, , 3 (4) 6, , 1.5     4 3 如果在a与c中间插入一个数b，使a，b，c组成一 个等比数列，则中间的数b叫做a与c的等比中项，且 注意： (1)若实数a、c有等比中项，则a、c符号相同； (2)若实数a、c有等比中项，则该等比中项必有两个值 2 ( )b ac b ac  或 若b2=ac，则a，b，c一定 成等比数列吗？ 若三个数为x，2x+2，3x+3成等比数列，则x=__-4 2、等比中项： 二、基础知识讲解 ∵n=1时上式仍成立 2 1 ,a a q 1 1 ( *)n na a q n N  3 2a a q 2 1a q 4 3a a q 3 1a q 即通项公式为: 分析：依等比数列的定义有 不完全归纳法 思考：等比数列{an}首项是a1，公比是q，如何表示an？ 1 1 n na a q   3 2 12 4 1 2 3 3 2 1 n n n n n n a a a aa aq q q q q qa a a a a a           ， ， ， ， ， ， 叠加法 等差数列{an}，公差为d 2 1 3 2 4 3 1 ( 1) ... n n a a d a a d a a d n a a d              个 1 ( 1) ,( 2)na a n d n    等比数列 思考：等比数列{an}首项是a1，公比是q，如何表示an？ 1 1 1 1 ,n nn n a q a a qa    即 ∵n=1时上式仍成立 n－1个 3 2 12 4 1 2 3 3 2 1 n n n n n n a a a aa a a a a a a a             思考：等比数列{an}首项是a1，公比是q，如何表示an？ 3 2 12 4 1 2 3 3 2 1 n n n n n n a a a aa aq q q q q qa a a a a a           ， ， ， ， ， ， 分析：依等比数列的定义有 1nq  即通项公式为：an=a1qn-1 叠 乘 法 3、等比数列的通项公式： 二、基础知识讲解 an=a1qn-1 求等比数列的通项公式关键是求出首项和公比     1 -2 -4 -8 -16 2 1 -1,1 -1 1 求出下列等比数列的通项公式： ， 练 ， ， ； ， ， 习 ： ； 2n na   1( 1)n na   1 , , , 4 4 4 na q n a通项公式含有 这 个量，如果已知三个量， 第 个量就是未知数，通项公式就是方程，解方程就 可以求出第 个量。即利用方程思想“知三求一”。 把②的两边分别除以①的两边，得 解：设这个等比数列的首项是 a1，公比是 q，那么 2 1 12a q  3 1 18a q  ① ② 3 2q  例1、一个等比数列的第3项与第4项分别是12与18，求 它的第1项与第2项. 设 列 求 方 程 思 想 2 1 16 3 83 2a a q   因此， 三、例题分析 ③ 把③代入①，得 1 6 3a  练习2：在等比数列{an}中， （1）a1=3，an=192，q=2，求n； （2） a3=12，a4=18，求a1和a2； （3）a3=48，a7=3，求a1和q ； （4）a1+a2=3， a4+a5=24，求an； n=7 1 1192, 2a q   an =2n-1 1 2 16 , 83a a  3、等比数列的通项公式： 二、基础知识讲解 an=a1qn-1 注意：在用等比数列的通项公式求公比q时， 应特别注意开方运算后q的符号！ 思考：我们知道，等差数列{an}满足下列公式 （1）an=ak+(n-k)d； （2）若m+n=p+q，则am+an =ap+aq 那么，等比数列是否也有类似的公式呢？ 在等比数列{an}中 （1）an=akqn-k； （2）若m+n=k+l，则am·an =ak·al *(2 , , ),mm n k n k N  特别地，若 在等比数列{an}中，若m+n=k+l，则am·an =ak·al 2 m n ka a a则 二、基础知识讲解 1 9 3 7 11 { } 0 64 20 n na a a a a a a     例 在等比数列 中， ，且 ， ，求 2： 。 3 7 1 9 3 7 64 20 a a a a a a      依题意可解 得： 3 3 7 7 4 16 16 4 a a a a        解得 或 3 4 7 4 416 a qa    当 时， ， 4 11 7 64a a q  3 4 7 16 1 44 a qa    当 时， ， 4 11 7 1a a q  三、例题分析 (1)若a7·a12=5，则a8·a9·a10·a11=______. (2)在等比数列{an}中，若a3=4，a7=9，则a5=_______. (3)已知是等比数列，且an>0，a2a4+2a3a5+a4a6=25， 那么a3+a5= ( ) A.5 B.10 C.15 D.20 25 A 6 四、课时练习 1.定义 2.公比(差) 3.等比(差) 中项 4.通项公式 daa nn 1 q≠0d∈R 等比中项 abG 2 等差中项 baA 2 1 1  n n qaadnaan )1(1  等差数列 qa a n n 1 等比数列 四、课时小结 1、课本P53A组第1题 五、作业 2、若lga，lgb，lgc成等差数列，则a，b，c成 数列等比 拓展：若 a，b，c成等比数列，则lga，lgb，lgc是否 一定成等差数列？ 不一定，只有当a，b，c都大于0才成立 1、若2a，2b，2c成等比数列，则a，b，c成 数列等差 六、思考题 2 5 2 3 { } 2 128 (1) (2) log { } 360 n n n n n n n a a a a b a b n S S n     、已知等比数列 中， ， 。 求通项公式 ； 若 ，数列 的前 项和为 ，且 ，求 的值。