2018-2019学年黑龙江省鹤岗市第一中学高二上学期期末考试数学（理）试题 Word版

2018-2019学年黑龙江省鹤岗市第一中学高二上学期期末考试数学（理）试题 Word版

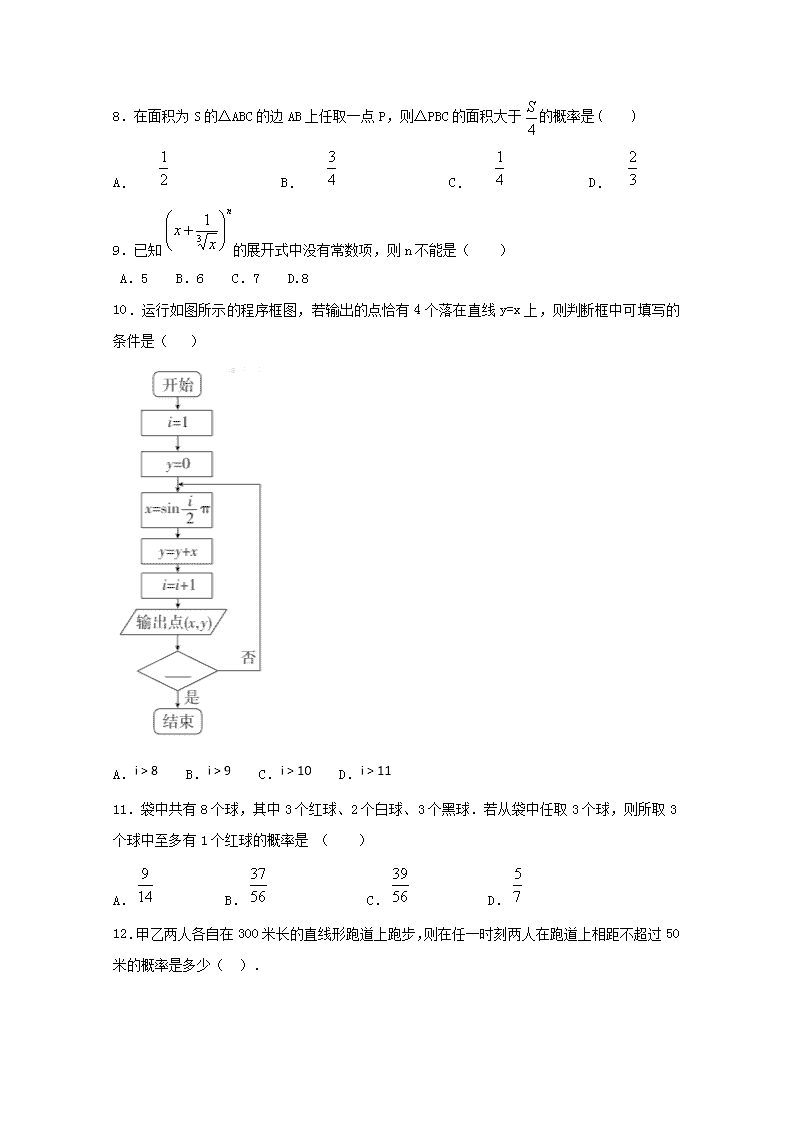
鹤岗一中2018-2019学年度上学期期末考试 高二数学试卷（理科）‎ 一、单选题 ‎1．命题“，使”的否定为（ ）‎ A．，使 B．，使 C．， D．，‎ ‎2．“a＞0”是“|a|＞0”的（ ）‎ A． 充分不必要条件 B． 必要不充分条件 C． 充要条件 D． 既不充分也不必要条件 ‎3．有50件产品，编号为0，1，2，…，49，现从中抽取5个进行检验，用系统抽样的方法抽取样本的编号可以为( )‎ A．5，10，15，20，25 B．5，13，21，29，37 C．8，22，23，1，20 D．1，11，21，31，41‎ ‎4．已知x、y的取值如下表所示：‎ x ‎0‎ ‎1‎ ‎3‎ ‎4‎ y ‎2.2‎ ‎4.3‎ ‎4.8‎ ‎6.7‎ 若从散点图分析，y与x线性相关，且，则的值等于 （ ）‎ A．2.6 B．6.3 C．2 D．4.5‎ ‎5．与二进制数相等的十进制数是（ ）‎ A．6 B．7 C．10 D．11‎ ‎6．下列说法中，正确的是（ ）‎ A．数据5,4,4,3,5,2的众数是4‎ B．一组数据的标准差是这组数据的方差的平方 C．数据2,3,4,5的标准差是数据4,6,8,10的标准差的一半 D．频率分布直方图中各小长方形的面积等于相应各组的频数 ‎7．5个人站成一排，若甲、乙两人之间恰有1人，则不同的站法数有（ ）‎ A．18 B．26 C．36 D．48‎ ‎8．在面积为S的△ABC的边AB上任取一点P，则△PBC的面积大于的概率是( )‎ A． 　 　　　 B． 　 　　 C． 　 　　 D．　‎ ‎9．已知的展开式中没有常数项，则n不能是（ ） ‎ ‎ A．5 B．6 C．7 D.8‎ ‎10．运行如图所示的程序框图，若输出的点恰有4个落在直线y=x上，则判断框中可填写的条件是（ ）‎ A． B． C． D．‎ ‎11．袋中共有8个球，其中3个红球、2个白球、3个黑球．若从袋中任取3个球，则所取3个球中至多有1个红球的概率是 （ ）‎ A． B． C． D． ‎ ‎12．甲乙两人各自在300米长的直线形跑道上跑步，则在任一时刻两人在跑道上相距不超过50米的概率是多少（ ）． ‎ ‎ A． B． C． D． ‎ 二、填空题 ‎13．某校老年、中年和青年教师的人数见下表，采用分层抽样的方法调查教师的身体状况，在抽取的样本中，青年教师有320人，则该样本的老年教师人数为____________．‎ 类别 老年教师 中年教师 青年教师 合计 人数 ‎900‎ ‎1800‎ ‎1600‎ ‎4300‎ ‎14．已知,当时，用秦九韶算法求=______________．‎ ‎15．的展开式中常数项是________．‎ ‎16．某翻译处有8名翻译，其中有小张等3名英语翻译，小李等3名日语翻译，另外2名既能翻译英语又能翻译日语，现需选取5名翻译参加翻译工作，3名翻译英语，2名翻译日语，且小张与小李恰有1人选中，则有________种不同选取方法.‎ 三、解答题 ‎17．已知命题；命题，若为真命题，求的取值范围．‎ ‎18．若的展开式的二项式系数和为128.‎ ‎(Ⅰ)求的值; ‎ ‎(Ⅱ) 求展开式中二项式系数的最大项. ‎ ‎19．一个盒子中装有四张卡片，每张卡片上写有一个数字，数字分别是1,2,3,4,现从盒子中随机抽取卡片，每张卡片被抽到的概率相等.‎ ‎（1）若一次抽取三张卡片，求抽到的三张卡片上的数字之和大于7的概率；‎ ‎（2）若第一次抽一张卡片，放回后搅匀再抽取一张卡片，求两次抽取中至少有一次抽到写有数字3的卡片的概率.‎ ‎20．去年年底，某商业集团公司根据相关评分细则，对其所属25‎ 家商业连锁店进行了考核评估.将各连锁店的评估分数按[60,70), [70,80), [80,90), [90,100),分成四组，其频率分布直方图如下图所示，集团公司依据评估得分，将这些连锁店划分为A,B,C,D四个等级，等级评定标准如下表所示.‎ ‎（1）估计该商业集团各连锁店评估得分的众数和平均数；‎ ‎（2）从评估分数不小于80分的连锁店中任选2家介绍营销经验，求至少选一家A等级的概率.‎ ‎21．某种产品的广告费支出与销售额(单位：万元）具有较强的相关性，且两者之间有如下对应数据:‎ ‎2‎ ‎4‎ ‎5‎ ‎6‎ ‎8‎ ‎28‎ ‎36‎ ‎52‎ ‎56‎ ‎78‎ ‎（1）求关于的线性回归方程； ‎ ‎（2）根据（1）中的线性回归方程，当广告费支出为10万元时，预测销售额是多少？‎ 参考数据： ，，。‎ 附：回归方程中斜率和截距的最小二乘估计公式分别为：‎ ‎，.‎ ‎22．如图，椭圆C1： （a＞b＞0）的离心率为，x轴被曲线C2：y=x2‎ ‎﹣b截得的线段长等于C1的长半轴长．‎ ‎（1）求a,b的值；‎ ‎（2）设C2与y轴的交点为M，过坐标原点O的直线l与C2相交于点A、B，直线MA，MB分别与C1相交于D，E，证明：MD⊥ME. 并记△MAB，△MDE的面积分别是S1，S2．问：是否存在直线l，使得？若存在，求出直线l的方程；若不存在，请说明理由．‎ 高二数学理科试题答案 一、选择题 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ D A ‎ D ‎ A ‎ A C ‎ C B ‎ B ‎ A ‎ D ‎ B 二、填空题 ‎13、180 14、24 15、-161 16、29‎ 三、解答题 ‎17. ‎ ‎18. (Ⅰ) ；(Ⅱ) .‎ ‎19. (1)；(2).‎ ‎20.（1）估计评估得分的众数为75分．‎ 估计该商业集团各连锁店评估得分平均数为：75.4‎ ‎（2）等级的频数为：，记这两家分别为等级的频数为：，记这四家分别为：从这6家连锁店中任选2家，共有，，，，共15种选法．记事件{至少选一家等级}则事件包含：，共9种．∴‎ ‎21. （1）（2）当广告费支出为10万元时，预测销售额大约为.‎ ‎（1）， ， ‎ ‎ 因此所求回归直线方程为 ‎ ‎(2)当时， 答：当广告费支出为10万元时，预测销售额大约为. ‎ ‎22. （1）2，1；（2）存在，或.（1）由题得e=，从而a=2b，又2=a，解得a=2，b=1.（2）由题得，直线l的斜率存在，设为k，则直线l的方程为y=kx，由得x2-kx-1=0．设A（x1，y1），B（x2，y2），则x1，x2是上述方程的两个实根，于是x1+x2=k，x1x2=-1，又点M的坐标为（0， -1），‎ 所以kMA•kMB=====-1．故MA⊥MB，即MD⊥ME．设直线MA的斜率为k1，则直线MA的方程为y=k1x-1．由，解得或．则点A的坐标为（k1，k12-1）．又直线MB的斜率为-，同理可得点B的坐标为（-， -1）．于是s1=|MA|•|MB|= •|k1|••|-|=．由得（1+4k12）x2-8k1x=0．解得或，，则点D的坐标为,又直线ME的斜率为-．同理可得点E的坐标为．于是s2=|MD|•|ME|=．故 ‎=，解得k12=4或k12=．又由点A，B的坐标得，k==k1-．所以k=±．故满足条件的直线存在，且有两条，其方程为y=x和y=-x．‎