2018版高考文科数学(北师大版)一轮文档讲义:章2-6对数与对数函数
第6讲 对数与对数函数
最新考纲 1.理解对数的概念及其运算性质,知道用换底公式将一般对数转化成自然对数或常用对数;了解对数在简化运算中的作用;2.理解对数函数的概念及其单调性,掌握对数函数图像通过的特殊点,会画底数为2,10,的对数函数的图像;3.体会对数函数是一类重要的函数模型.4.了解指数函数y=ax(a>0,且a≠1)与对数函数y=logax(a>0,且a≠1)互为反函数.
知 识 梳 理
1.对数的概念
一般地,如果a(a>0,a≠1)的b次幂等于N,即ab=N,那么数b叫作以a为底N的对数,记作logaN=b.其中a叫作对数的底数,N叫作真数.
2.对数的性质、换底公式与运算性质
(1)对数的性质:①alogaN=N;②logaab=b(a>0,且a≠1)
(2)对数的运算法则
如果a>0且a≠1,M>0,N>0,那么
①loga(MN)=logaM+logaN;
②loga=logaM-logaN;
③logaMn=nlogaM(n∈R);
④loga mMn=logaM(m,n∈R,且m≠0).
(3)对数的重要公式
①换底公式:logbN=(a,b均大于零且不等于1);
②logab=,推广logab·logbc·logcd=logad.
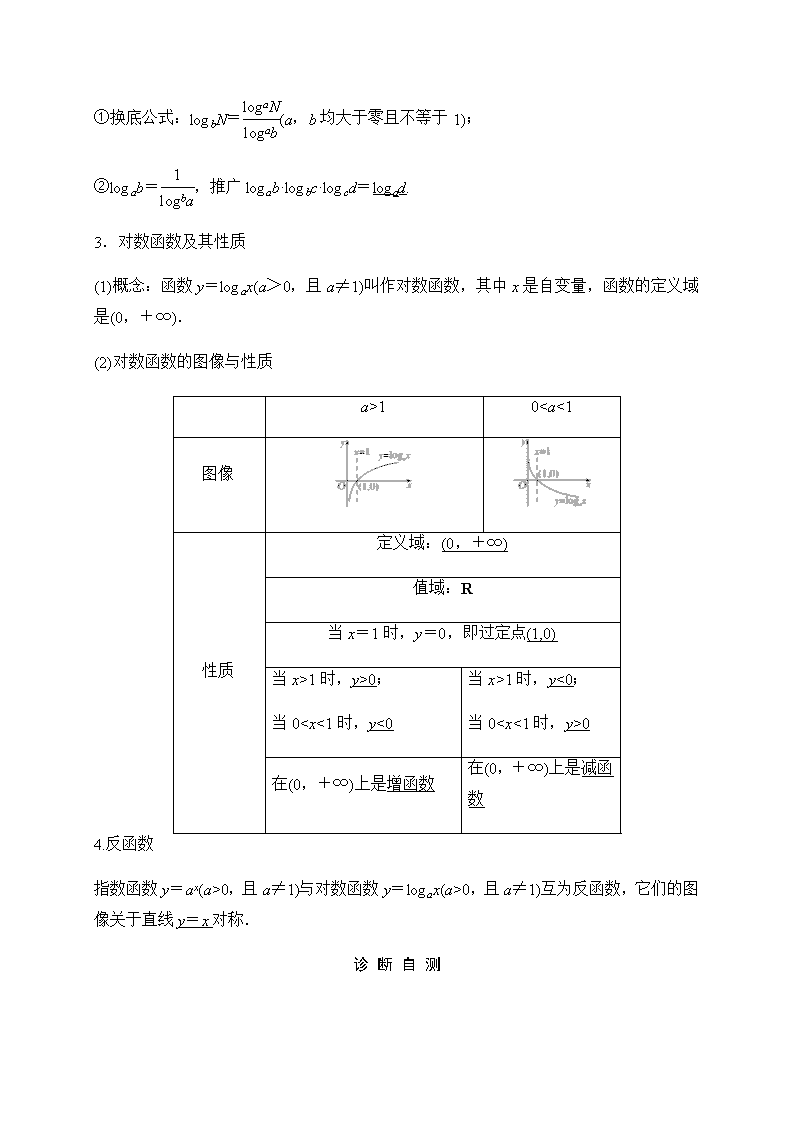
3.对数函数及其性质
(1)概念:函数y=logax(a>0,且a≠1)叫作对数函数,其中x是自变量,函数的定义域是(0,+∞).
(2)对数函数的图像与性质
a>1
0
1时,y>0;
当01时,y<0;
当00
在(0,+∞)上是增函数
在(0,+∞)上是减函数
4.反函数
指数函数y=ax(a>0,且a≠1)与对数函数y=logax(a>0,且a≠1)互为反函数,它们的图像关于直线y=x对称.
诊 断 自 测
1.判断正误(在括号内打“√”或“×”) 精彩PPT展示
(1)log2x2=2log2x.( )
(2)函数y=log2(x+1)是对数函数( )
(3)函数y=ln与y=ln(1+x)-ln(1-x)的定义域相同.( )
(4)当x>1时,若logax>logbx,则a0,且a≠1)的图像如图,则下列结论成立的是( )
A.a>1,c>1 B.a>1,01 D.00,即logac>0,所以0b>c B.a>c>b
C.c>b>a D.c>a>b
解析 ∵01.
∴c>a>b.
答案 D
4.(2015·浙江卷)计算:log2=________;2log23+log43=________.
解析 log2=log2-log22=-1=-;
2log23+log43=2log23·2log43=3×2log43=3×2log2=3.
答案 - 3
5.若loga<1(a>0,且a≠1),则实数a的取值范围是________.
解析 当01时,loga1.
答案 ∪(1,+∞)
考点一 对数的运算
【例1】 (1)设2a=5b=m,且+=2,则m等于( )
A. B.10 C.20 D.100
(2)计算:÷100=________.
解析 (1)由已知,得a=log2m,b=log5m,
则+=+=logm2+logm5=logm10=2.
解得m=.
(2)原式=(lg 2-2-lg 52)×100=lg×10=lg 10-2×10=-2×10=-20.
答案 (1)A (2)-20
规律方法 (1)在对数运算中,先利用幂的运算把底数或真数进行变形,化成分数指数幂的形式,使幂的底数最简,然后正用对数运算法则化简合并.
(2)先将对数式化为同底数对数的和、差、倍数运算,然后逆用对数的运算法则,转化为同底对数真数的积、商、幂再运算.
(3)ab=N⇔b=logaN(a>0,且a≠1)是解决有关指数、对数问题的有效方法,在运算中应注意互化.
【训练1】 (1)(2017·北京东城区综合练习)已知函数f(x)=则f(2+log23)的值为( )
A.24 B.16 C.12 D.8
(2)(2015·安徽卷)lg+2lg 2--1=________.
解析 (1)因为3<2+log23<4,所以f(2+log23)=f(3+log23)=23+log23=8×2log23=24.
(2)lg+2lg 2--1=lg 5-lg 2+2lg 2-2=lg 5+lg 2-2=lg 10-2=-1.
答案 (1)A (2)-1
考点二 对数函数的图像及应用
【例2】 (1)(2017·郑州一模)若函数y=a|x|(a>0,且a≠1)的值域为{y|y≥1},则函数y=loga|x|的图像大致是( )
(2)(2017·宝鸡调研)已知函数f(x)=且关于x的方程f(x)+x-a=0有且只有一个实根,则实数a的取值范围是________.
解析 (1)由于y=a|x|的值域为{y|y≥1},
∴a>1,则y=logax在(0,+∞)上是增函数,
又函数y=loga|x|的图像关于y轴对称.
因此y=loga|x|的图像应大致为选项B.
(2)
如图,在同一坐标系中分别作出y=f(x)与y=-x+a的图像,其中a表示直线在y轴上截距.
由图可知,当a>1时,直线y=-x+a与y=log2x只有一个交点.
答案 (1)B (2)a>1
规律方法 (1)在识别函数图像时,要善于利用已知函数的性质、函数图像上的特殊点(与坐标轴的交点、最高点、最低点等)排除不符合要求的选项.
(2)一些对数型方程、不等式问题常转化为相应的函数图像问题,利用数形结合法求解.
【训练2】 (1)函数y=2log4(1-x)的图像大致是( )
(2)当01时,不符合题意,舍去.
所以实数a的取值范围是.
答案 (1)C (2)B
考点三 对数函数的性质及应用(多维探究)
命题角度一 比较对数值的大小
【例3-1】 (2016·全国Ⅰ卷)若a>b>0,0cb
解析 由y=xc与y=cx的单调性知,C、D不正确.
∵y=logcx是减函数,得logca0且a≠1,故必有a2+1>2a,
又loga(a2+1)1,∴a>.综上,a∈.
答案 C
命题角度三 对数型函数的性质
【例3-3】 已知函数f(x)=loga(3-ax).
(1)当x∈[0,2]时,函数f(x)恒有意义,求实数a的取值范围;
(2)是否存在这样的实数a,使得函数f(x)在区间[1,2]上为减函数,并且最大值为1?如果存在,试求出a的值;如果不存在,请说明理由.
解 (1)∵a>0且a≠1,设t(x)=3-ax,
则t(x)=3-ax为减函数,
x∈[0,2]时,t(x)的最小值为3-2a,
当x∈[0,2]时,f(x)恒有意义,
即x∈[0,2]时,3-ax>0恒成立.
∴3-2a>0.∴a<.
又a>0且a≠1,∴a∈(0,1)∪.
(2)t(x)=3-ax,∵a>0,
∴函数t(x)为减函数.
∵f(x)在区间[1,2]上为减函数,∴y=logat为增函数,
∴a>1,x∈[1,2]时,t(x)最小值为3-2a,f(x)最大值为f(1)=loga(3-a),
∴即
故不存在这样的实数a,使得函数f(x)在区间[1,2]上为减函数,并且最大值为1.
规律方法 (1)确定函数的定义域,研究或利用函数的性质,都要在其定义域上进行.
(2)如果需将函数解析式变形,一定要保证其等价性,否则结论错误.
(3)在解决与对数函数相关的比较大小或解不等式问题时,要优先考虑利用对数函数的单调性来求解.在利用单调性时,一定要明确底数a的取值对函数增减性的影响,及真数必须为正的限制条件.
【训练3】 (1)设a=log32,b=log52,c=log23,则( )
A.a>c>b B.b>c>a
C.c>b>a D.c>a>b
(2)已知函数f(x)=loga(8-ax)(a>0,且a≠1),若f(x)>1在区间[1,2]上恒成立,则实数a的取值范围是________.
解析 (1)a=log32log22=1,
所以,c最大.
由1,即a>b,
所以c>a>b.
(2)当a>1时,f(x)=loga(8-ax)在[1,2]上是减函数,由f(x)>1在区间[1,2]上恒成立,
则f(x)min=loga(8-2a)>1,
解之得11在区间[1,2]上恒成立,
则f(x)min=loga(8-a)>1,且8-2a>0.
∴a>4,且a<4,故不存在.
综上可知,实数a的取值范围是.
答案 (1)D (2)
[思想方法]
1.对数值取正、负值的规律
当a>1且b>1或00;
当a>1且01时,logab<0.
2.利用单调性可解决比较大小、解不等式、求最值等问题,其基本方法是“同底法”,即把不同底的对数式化为同底的对数式,然后根据单调性来解决.
3.比较幂、对数大小有两种常用方法:(1)数形结合;(2)找中间量结合函数单调性.
4.多个对数函数图像比较底数大小的问题,可通过比较图像与直线y=1交点的横坐标进行判定.
[易错防范]
1.在对数式中,真数必须是大于0的,所以对数函数y=logax的定义域应为(0,+∞).对数函数的单调性取决于底数a与1的大小关系,当底数a与1的大小关系不确定时,要分01两种情况讨论.
2.在运算性质logaMα=αlogaM中,要特别注意条件,在无M>0的条件下应为logaMα=αloga|M|(α∈N+,且α为偶数).
3.解决与对数函数有关的问题时需注意两点:(1)务必先研究函数的定义域;(2)注意对数底数的取值范围.
基础巩固题组
(建议用时:40分钟)
一、选择题
1.(2015·四川卷)设a,b为正实数,则“a>b>1”是“log2a>log2b>0”的( )
A.充分必要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
解析 因为y=log2x在(0,+∞)上单调递增,所以当a>b>1时,有log2a>log2b>log21=0;
当log2a>log2b>0=log21时,有a>b>1.
答案 A
2.(2017·上饶模拟)已知a=log23+log2,b=log29-log2,c=log32,则a,b,c的大小关系是( )
A.a=bc
C.ab>c
解析 因为a=log23+log2=log23=log23>1,b=log29-log2=log23=a,c=log320,且a≠1)的图像如图所示,则下列函数图像正确的是( )
解析 由题意y=logax(a>0,且a≠1)的图像过(3,1)点,可解得a=3.选项A中,y=3-x=x,显然图像错误;选项B中,y=x3,由幂函数图像可知正确;选项C中,y=(-x)3=-x3,显然与所画图像不符;选项D中,y=log3(-x)的图像与y=log3x的图像关于y轴对称,显然不符.故选B.
答案 B
4.已知函数f(x)=则f(f(1))+f的值是( )
A.5 B.3 C.-1 D.
解析 由题意可知f(1)=log21=0,
f(f(1))=f(0)=30+1=2,
f=+1=3log32+1=2+1=3,
所以f(f(1))+f=5.
答案 A
5.(2016·浙江卷)已知a,b>0且a≠1,b≠1,若logab>1,则( )
A.(a-1)(b-1)<0 B.(a-1)(a-b)>0
C.(b-1)(b-a)<0 D.(b-1)(b-a)>0
解析 ∵a>0,b>0且a≠1,b≠1.
由logab>1得loga>0.
∴a>1,且>1或0a>1或00.
答案 D
二、填空题
6.设f(x)=log是奇函数,则使f(x)<0的x的取值范围是________.
解析 由f(x)是奇函数可得a=-1,
∴f(x)=lg,定义域为(-1,1).
由f(x)<0,可得0<<1,∴-10,且a≠1)的值域是[4,+∞),则实数a的取值范围是________.
解析 当x≤2时,f(x)≥4;又函数f(x)的值域为[4,+∞),所以解1<a≤2,所以实数a的取值范围为(1,2].
答案 (1,2]
三、解答题
9.设f(x)=loga(1+x)+loga(3-x)(a>0,a≠1),且f(1)=2.
(1)求a的值及f(x)的定义域;
(2)求f(x)在区间上的最大值.
解 (1)∵f(1)=2,
∴loga4=2(a>0,a≠1),
∴a=2.
由得-1<x<3,
∴函数f(x)的定义域为(-1,3).
(2)f(x)=log2(1+x)+log2(3-x)
=log2(1+x)(3-x)=log2[-(x-1)2+4],
∴当x∈(-1,1]时,f(x)是增函数;
当x∈(1,3)时,f(x)是减函数,
故函数f(x)在上的最大值是f(1)=log24=2.
10.(2016·榆林月考)已知函数f(x)是定义在R上的偶函数,且f(0)=0,当x>0时,f(x)=x.
(1)求函数f(x)的解析式;
(2)解不等式f(x2-1)>-2.
解 (1)当x<0时,-x>0,则f(-x)=(-x).
因为函数f(x)是偶函数,所以f(-x)=f(x)=(-x),
所以函数f(x)的解析式为
(2)因为f(4)=4=-2,f(x)是偶函数,
所以不等式f(x2-1)>-2转化为f(|x2-1|)>f(4).
又因为函数f(x)在(0,+∞)上是减函数,
所以|x2-1|<4,解得-p D.p=r>q
解析 ∵0,
又∵f(x)=ln x在(0,+∞)上为增函数,
∴f>f(),即q>p.
又r=(f(a)+f(b))=(ln a+ln b)=ln=p,
故p=rb>1,若logab+logba=,ab=ba,则a=________,b=________.
解析 ∵logab+logba=logab+=,
∴logab=2或.
∵a>b>1,∴logab0,且a≠1)的最大值是1,最小值是-,求a的值.
解 由题意知f(x)=(logax+1)(logax+2)
=(logx+3logax+2)
=2-.
当f(x)取最小值-时,logax=-.
又∵x∈[2,8],∴a∈(0,1).
∵f(x)是关于logax的二次函数,
∴函数f(x)的最大值必在x=2或x=8时取得.
若2-=1,则a=2,
此时f(x)取得最小值时,x==∉[2,8],舍去.
若2-=1,则a=,
此时f(x)取得最小值时,x=-=2∈[2,8],
符合题意,∴a=.
特别提醒:教师配赠习题、课件、视频、图片、文档等各种电子资源见《创新设计·高考总复习》光盘中内容.