2013陕西中考数学试题及答案word版

2013陕西中考数学试题及答案word版

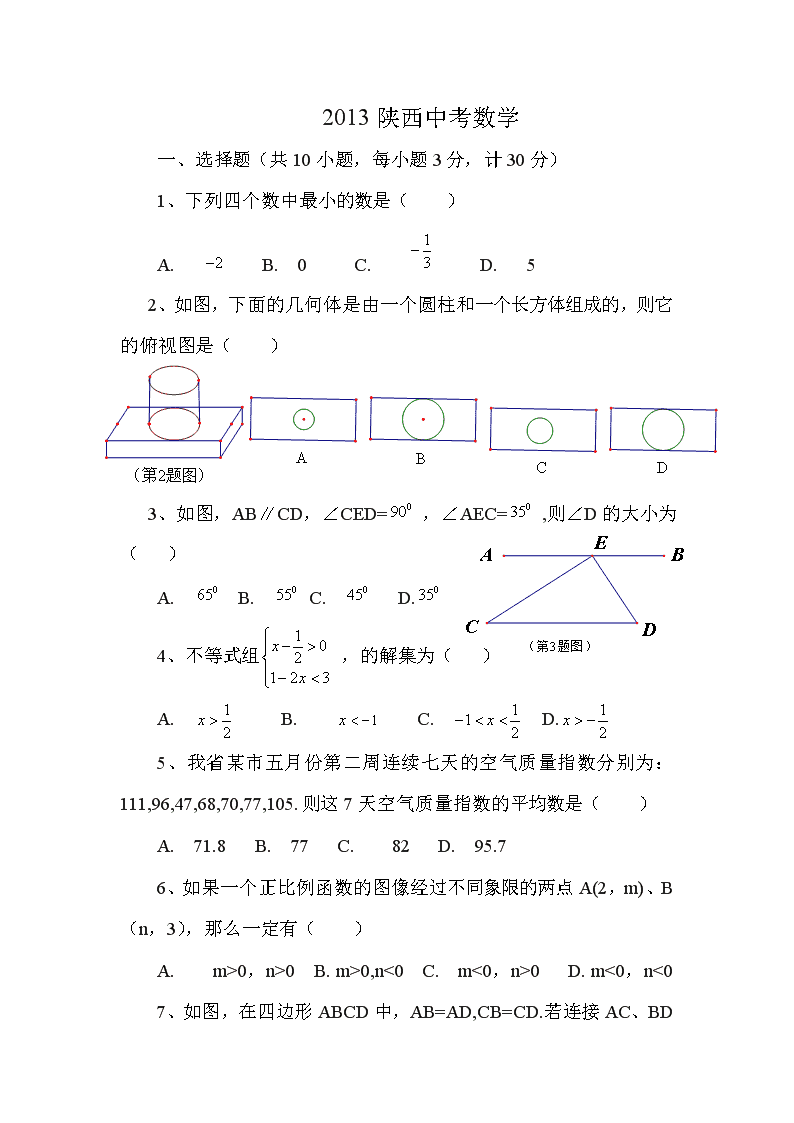
‎2013陕西中考数学 一、选择题（共10小题，每小题3分，计30分）‎ ‎1、下列四个数中最小的数是（ ）‎ A. B. 0 C. D. 5‎ ‎2、如图，下面的几何体是由一个圆柱和一个长方体组成的，则它的俯视图是（ ）‎ ‎3、如图，AB∥CD，∠CED= ，∠AEC= ,则∠D的大小为（ ）‎ A. B. C. D. ‎ ‎4、不等式组 ，的解集为（ ）‎ A. B. C. D. ‎ ‎5、我省某市五月份第二周连续七天的空气质量指数分别为：111,96,47,68,70,77,105.则这7天空气质量指数的平均数是（ ）‎ A. 71.8 B. 77 C. 82 D. 95.7 ‎ ‎6、如果一个正比例函数的图像经过不同象限的两点A(2，m)、B（n，3），那么一定有（ ）‎ A. m>0，n>0 B. m>0,n<0 C. m<0，n>0 D. m<0，n<0‎ ‎7、如图，在四边形ABCD中，AB=AD,CB=CD.若连接AC、BD相交于点O，则图中全等三角形共有（ ）‎ A. 1对 B. 2对 C. 3对 D. 4对 ‎ ‎8、根据下表中一次函数的自变量 与函数的对应值，可得的值为（ ）‎ ‎ ‎ ‎ ‎ ‎0‎ ‎1‎ ‎ ‎ ‎3‎ ‎ ‎ ‎0‎ A. 1 B. C. 3 D. ‎ ‎9、如图，在矩形ABCD中，AD=2AB，点M,N分别在AD、BC上，连接BM、DN.若四边形MBDN是菱形，则 等于（ ）‎ A. B. C. D. ‎ ‎10、已知两点A B 均在抛物线 上，点C 是该抛物线的顶点.若 ，则 的取值范围是（ ）‎ A. B. C. D. ‎ 二、填空题（共6小题，每小题3分，计18分）‎ ‎11、计算： = ‎ ‎12、一元二次方程 的根是 ‎ ‎13、请从以下两个小题中任选一个作答，若多选，则按所得的第一题计分 A、在平面直角坐标系中，线段AB的两个端点的坐标分别为A ‎ ，B ,将线段AB经过平移后得到线段 .若点A的对应点为 ,则点B的对应点 的坐标是 ‎ B、比较大小： （填“ >”,“=”或“<”）‎ ‎14、如图，四边形ABCD的对角线AC、BD相交于点O，且BD平分AC.若BD=8，AC=6，∠BOC= ,则四边形ABCD的面积为 （结果保留根号）‎ ‎15、如果一个正比例函数的图像与反比例函数 的图像交与A 、B 两点，那么 的值为 .‎ ‎16、如图，AB是⊙O的一条弦，点C是⊙O上一动点，且∠ACB= ，点E、F分别是AC、BC的中点，直线EF与⊙O交于G、H两点.若⊙O的半径为7，则GE+FH的最大值为 ‎ 三、解答题（共9小题，计72分）‎ ‎17、（本题满分5分）解分式方程： ‎ ‎18、（本题满分6分）如图，∠AOB= ，OA=OB，直线 经过点O,分别过A、B两点作AC⊥ 于点C,BD⊥ 交 于点D.‎ 求证：AC=OD.‎ ‎19、（本题满分7分）我省教育厅发了《在全省中小学幼儿园广泛开展节约教育的通知》，通知中要求各学校全面持续开展“光盘行动”.‎ 某市教育局督导检查组为了调查学生对“节约教育”内容的了解程度（程度分为：“A-了解很多”，“B-了解较多”，“C-了解较少”，“D-不了解”），对本市一所中学的学生进行了抽样调查我们将这次调查的结果绘制了以下两幅统计图.‎ 根据以上信息，解答下列问题：‎ （1） 本次抽样调查了多少名学生？‎ （2） 补全两幅统计图；‎ （3） 若该中学共有1800名学生，请你估计这所中学的所有学生中，对“节约教育”内容“了解较多”的有多少名？‎ 被抽查学生对“节约教育”内容了解程度的统计图 ‎20、（本题满分8分）一天晚上，李明和张龙利用灯光下的影子长来测量一路灯D的高度.如图，当李明走到点A处时，张龙测得李明直立时升高AM与其影子长AE正好相等；接着李明沿AC方向继续向前走，走到点B处时，李明直立时的升高1.75m，求路灯的高CD的长。（结果精确到0.1m）‎ ‎21、（本题满分8分）“五一节”期间，申老师一家自驾游去了离家170千米的某地.下面是他们离家的距离（千米）与汽车行驶时间（小时）之间的函数图象.‎ ‎（1）求他们出发半小时时，离家多少千米？‎ ‎（2）求出AB段图像的函数表达式；‎ ‎（3）他们出发2小时时，离目的地还有多少千米？‎ ‎22、（本题满分8分）甲、乙两人用手指玩游戏，规则如下：ⅰ ‎）每次游戏时，两人同时随机地各伸出一根手指；ⅱ）两人伸出的手指中，大拇指只胜食指、食指只胜中指、中指只胜无名指、无名指只胜小拇指、小拇指只胜大拇指，否则不分胜负.依据上述规则，当甲、乙两人同时随机的各伸出一根手指时，‎ ‎（1）求甲伸出小拇指取胜的概率；‎ ‎（2）求乙胜出的概率.‎ ‎23、（本题满分8分）如图，直线 与⊙O相切于点D，过圆心O作EF∥ 交⊙O于E、F两点，点A是⊙O上一点，连接AE、AF,并分别延长交直线 于B、C两点，‎ ‎（1）求证：∠ABC+∠ACB= ‎ ‎（2）当⊙O得半径R=5，BD=12时，‎ 求 的值.‎ ‎24、（本题满分10分）在平面直角坐标系中，一个二次函数的图像经过A（1,0）B（3,0）两点.‎ ‎（1）写出这个二次函数图像的对称轴；‎ ‎（2）设这个二次函数图像的顶点为D,与 轴交与点C，它的对称轴与 轴交与点E，连接AC、DE和DB.当△AOC与△DEB相似时，求这个二次函数的表达式.‎ ‎[提示：如果一个二次函数的图像与 轴的交点为A B ，那么它的表达式可表示为 .]‎ ‎25、（本题满分12分）问题探究 ‎（1）请在图①中作出两条直线，使他们将圆面四等分；‎ ‎（2）如图②，M是正方形ABCD内一点，请在图②中作出两条直线（要求其中一条直线必须过点M）,使它们将正方形ABCD的面积四等分，并说明理由.‎ 问题解决 ‎（3）如图③，在四边形ABCD中，AB//CD，AB+CD=BC,点P是AD的中点.如果AB= ，CD= ，且 ，那么在边BC上是否存在一点Q,使PQ所在直线将正方形ABCD的面积分成相等的两部分？若存在，求出BQ的长；若不存在，说明理由.‎ ‎（第25题图①） （第25题图②） （第25题图③）‎ 参考答案 一、选择题 ADBAC DCACB 二、填空题 ‎11、 ‎ ‎12、0,3‎ ‎13、A（6,4）‎ B >‎ ‎ 14、 ‎ ‎ 15、24‎ ‎16、10.5‎ 三、解答题 ‎17、解：‎ ‎ ‎ ‎18、证明：‎ ‎ ‎ ‎19、解：（1）抽样调查的学生人数为：3630%=120（名）…（2分）‎ ‎ （2）B的人数：120×45%=54（名）‎ ‎ C的百分比： ‎ ‎ D的百分比： ‎ ‎ 补全两幅统计图如图所示。………………………………（5分）（略）‎ （1） 对“节约教育”内容“了解较多”的学生人数为：‎ ‎ 1800×45%=810（名）………………………（7分）‎ ‎20、解： ‎ ‎ ‎ 即 ‎ 解之，得 ‎ ‎∴路灯高CD约为6.1.………………………（8分）‎ ‎21、解：设OA段图像的函数表达式为 ‎ ∵当=1.5时，=90；‎ ‎ ∴1.5 =90.‎ ‎ ∴ =60.‎ ‎ ∴ ‎ ‎ ∴当=0.5时，=60×0.5=30.‎ ‎ ∴行驶半小时时，他们离家30千米，………（3分）‎ ‎（2）设AB段图像的函数表达式为 ………………（4分）‎ ‎∴A(1.5，90)，B(2.5，170)在AB上，‎ ‎∴ ‎ 解之，得 ‎ ‎ ………………………………（6分）‎ ‎（3）当=2时，=80×230=130.‎ ‎∴170130=40.‎ ‎∴他们出发2小时后，离目的地还有40千米。…………（8分）‎ ‎22、解：设A,B,C,D,E分别表示大拇指，食指，中指，无名指，小拇指，列表如下：‎ 乙 甲 A B C D E A AA AB AC AD AE B BA BB BC BD BE C CA CB CC CD CE D DA DB DC DD DE E EA EB EC ED EE 由表格可知，共有25种等可能的结果。‎ ‎（1）由上表可知，甲伸出小拇指取胜有1种可能。‎ ‎∴P（甲伸出小拇指取胜）= ………………………………（3分）‎ ‎（2）由上表可知，乙取胜有5种可能。‎ ‎∴P(乙取胜)= ……………………………………………（8分）‎ ‎23、（1）证明：∵EF是⊙O的直径，‎ ‎ ∴∠EAF= ，‎ ‎ ∴∠ABC+∠ACB=.…………………（3分）‎ ‎(2)解：连接OD,则OD⊥BD。……………………（4分）‎ ‎ 过点E作EH⊥BC, 垂足为点H，‎ ‎ EH//OD.‎ ‎ ∵EF//BC.OE=OD,‎ ‎ ∴四边形EODH是正方形…………………（6分）‎ ‎ ∴EH=HD=OD=5.‎ ‎ 又∵BD=12，∴BH=7。‎ 在Rt△BEH中，tan∠BEH= ,‎ 而∠ABC+∠BEH=,∠ABC+∠ACB=,‎ ‎∴∠ACB=∠BEH.‎ ‎∴tan∠ACB= ……………………………（8分）‎ ‎24、解：（1）二次函数图像的对称轴为直线 ……（2分）‎ ‎ （2）设二次函数的表达式为 …（3分）‎ ‎ 当时，; 当时，.‎ ‎ ∴点C坐标为（0，），顶点D坐标为（2，）‎ ‎ ∴OC=‎ ‎ 又∵A(1，0)B(2，0)‎ ‎ ∴OA=1，EB=1，DE= ……………（5分）‎ ‎ 当△AOC与△DEB相似时，‎ ‎①假设∠OCA=∠EBD,‎ 可得 ‎ ‎∴ ……………………（7分）‎ ‎②假设∠OCA=∠EDB,可得 ‎ ‎∴ 此方程无解……………………（8分）‎ 综上所述，所求二次函数的表达式为 ‎ 或………（10分）‎ ‎25、（1）如图①所示……………………………………………（2分）‎ ‎ （2）如图②，连接AC、BD相交于点O，作直线OM分别交AD、BC于P、Q两点，过点O作OM的垂线分别交AB、CD于E、F两点，则直线OM、EF将正方形ABCD的面积四等分………………………（4分）‎ 理由如下：‎ ‎∵点O是正方形的对称中心.‎ ‎∴AP=CQ,EB=DF.‎ 在△AOP和△EOB中，‎ ‎∵∠AOP=∠AOE,∠BOE=∠AOE,‎ ‎∴∠AOP=∠BOE.‎ ‎∵OA=OB,∠OAP=∠EBO= ,‎ ‎∴△AOP△EOB.‎ ‎∴AP=BE=DF=CQ.‎ ‎∴AE=BQ=CF=PD. ………………………………（6分）‎ 设点O到正方形ABCD一边的距离 .‎ ‎∴ ‎ ‎∴ ‎ ‎∴直线EF、OM将正方形ABCD面积四等分……………（7分）‎ ‎（3）存在.当BQ=CD= 时，PQ将四边形ABCD面积二等分 ‎………………………………（6分）‎ 理由如下：‎ 如图③，延长BA到点E,使AE=,延长CD到点F，使DF= ，‎ 连接EF.‎ ‎∵ ,BE=BC= ，‎ ‎∴四边形EBCF是菱形，‎ 连接BF交AD于点M，则△MAB△MDF ‎∴AM=DM ‎∴P、M两点重合 ‎∴P点是菱形EBCF对角线的交点………………………………（10分）‎ 在BC上截取BQ=CD=,则CQ=AB=‎ 设点P到菱形EBCF一边的距离为，‎ 则 ‎ ‎∴‎ ‎∴当BQ=时，直线PQ将四边形ABCD的面积分成相等的两部分 ‎………（12分）‎ ‎（第25题图①） （第25题图②） （第25题图③）‎ ‎ ‎