- 2021-04-17 发布 |
- 37.5 KB |
- 16页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
人教版八年级上册数学同步练习课件-第13章-13等腰三角形
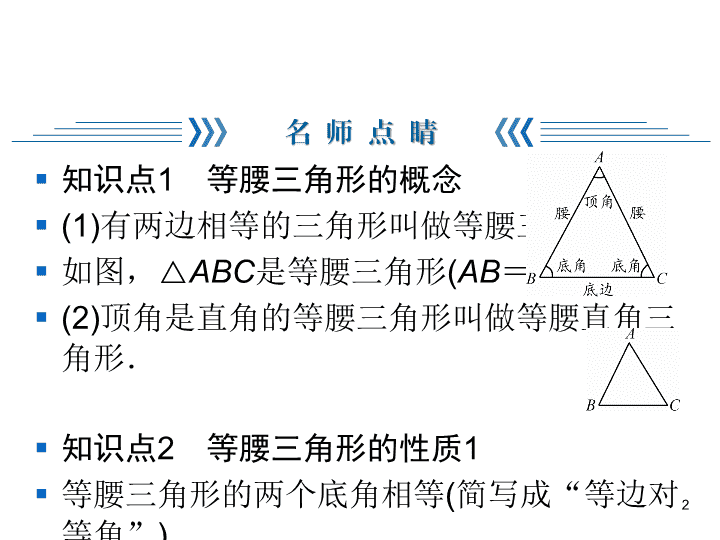
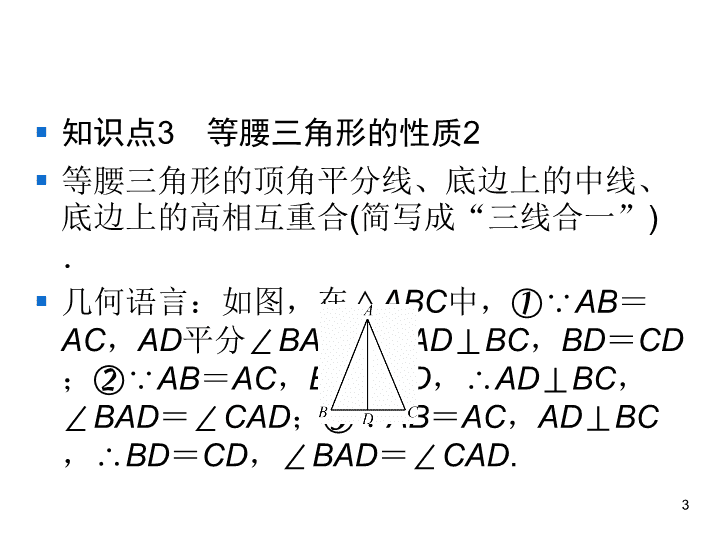
第十三章 轴对称 13.3 等腰三角形 第一课时 等腰三角形的性质 13.3.1 等腰三角形 § 知识点1 等腰三角形的概念 § (1)有两边相等的三角形叫做等腰三角形. § 如图,△ABC是等腰三角形(AB=AC). § (2)顶角是直角的等腰三角形叫做等腰直角三 角形. § 知识点2 等腰三角形的性质1 § 等腰三角形的两个底角相等(简写成“等边对 等角”). § 几何语言:如图,在△ABC中,∵AB=AC, ∴∠B=∠C. 2 § 知识点3 等腰三角形的性质2 § 等腰三角形的顶角平分线、底边上的中线、 底边上的高相互重合(简写成“三线合 一”). § 几何语言:如图,在△ABC中,①∵AB= AC,AD平分∠BAC,∴AD⊥BC,BD=CD; ②∵AB=AC,BD=CD,∴AD⊥BC, ∠BAD=∠CAD;③∵AB=AC,AD⊥BC, ∴BD=CD,∠BAD=∠CAD. 3 § 1.已知一个等腰三角形的顶角为80°,则 它的一个底角为( ) § A.30° B.50° § C.80° D.100° § 2.一个等腰三角形的两边长分别为4,8,则 它的周长为( ) § A.12 B.16 § C.20 D.16或20 4 B C § 3.如图,在△ABC中,AB=AC,过点A作AD∥BC.若∠1= 70°,则∠BAC的大小为( ) § A.30° B.40° § C.50° D.70° § 解析:∵AD∥BC,∠1=70°,∴∠C=∠1=70°.∵AB=AC, ∴∠B=∠C =70°,∴∠BAC=180°-∠B-∠C=180°- 70°-70°=40°. 5 B 4.如图,在△ABC中,AB=AC,AD⊥BC于点D.若 ∠BAC=80°,则∠BAD=___________.40° § 5.如图,在△ABC中,AB=AC, D是BC的中点,E、F分别是AB、 AC上的点,且AE=AF,求证: DE=DF. 6 7 § 7.【2018·浙江湖州中考】如图,AD、CE 分别是△ABC的中线和角平分线.若AB= AC,∠CAD=20°,则∠ACE的度数是( ) § A.20° § B.35° § C.40° § D.70° 8 B § 8.【2018·辽宁丹东中考】如图, 在△ABC中,AB=AC,AC的垂直 平分线交AC于点D,交AB于点E, 已知△BCE的周长为10,且BC=4, 则AB的长为( ) § A.3 B.4 § C.5 D.6 § 9.如图,在△ABC中,AB=AC, AD⊥BC,垂足为点D,E是AD上任 一点,则图中全等三角形的对数是( ) § A.4 B.3 § C.2 D.1 9 D B § 10.如图,在△ABC中,AB=AC,AD平分 ∠BAC,DE⊥AB,DF⊥AC,E、F分别为 垂足,则下列四个结论:①∠DEF=∠DFE; ②AE=AF;③DA平分∠EDF;④EF垂直平 分AD.其中正确的有( ) § A.1个 B.2个 § C.3个 D.4个 10 C § 11.如图,在△ABC中,AB=AC,AD是 BC边上的中线,CE⊥AB于点E.求证: ∠CAD=∠BCE. § 证明:∵AB=AC,BD=CD,∴∠B= ∠ACB,AD⊥BC. § ∵CE⊥AB,∴∠CAD+∠ACB=90°, ∠BCE+∠B=90°, § ∴∠CAD=∠BCE. 11 § 12.如图,在△ABC中,AB=AC, BD、CE是高,BD与CE相交于点O. § (1)求证:OB=OC; § (2)若∠ABC=50°,求∠BOC的 度数. 12 13 § 13.如果一个三角形能被一条线段分割成两 个等腰三角形,那么称这条线段为这个三角 形的特异线,称这个三角形为特异三角形. § (1)如图1,在△ABC中,∠B=2∠C,线段 AC的垂直平分线交AC于点D,交BC于点E. 求证:AE是△ABC的一条特异线; § (2)如图2,若△ABC是特异三角形,∠A= 30°,∠B为钝角,求出所有可能的∠B的度 数. 14 图1 图2 § (1)证明:∵DE垂直平分AC,∴EA=EC, ∴△EAC是等腰三角形,∴∠EAC=∠C, ∴∠AEB=∠EAC+∠C=2∠C.∵∠B= 2∠C,∴∠AEB=∠B,∴AB=AE, ∴△EAB是等腰三角形,∴AE是△ABC的一 条特异线. § (2)解:当BD是特异线时,如果AB=BD= DC,如图1,则∠ABC=∠ABD+∠DBC= 120°+15°=135°.如果AD=AB,DB= DC,如图2,则∠ABC=∠ABD+∠DBC= 75°+37.5°=112.5°. 15 § 如果AD=DB,DC=DB,如图3,则∠ABC=∠ABD+∠DBC= 30°+60°=90°(不合题意,舍去).当AD是特异线时,AB= BD,AD=DC,如图4,则∠ABC=180°-20°-20°=140°.当CD为特异线时,不合题意. § ∴符合条件的∠ABC的度数为135°或112.5°或140°. 16查看更多