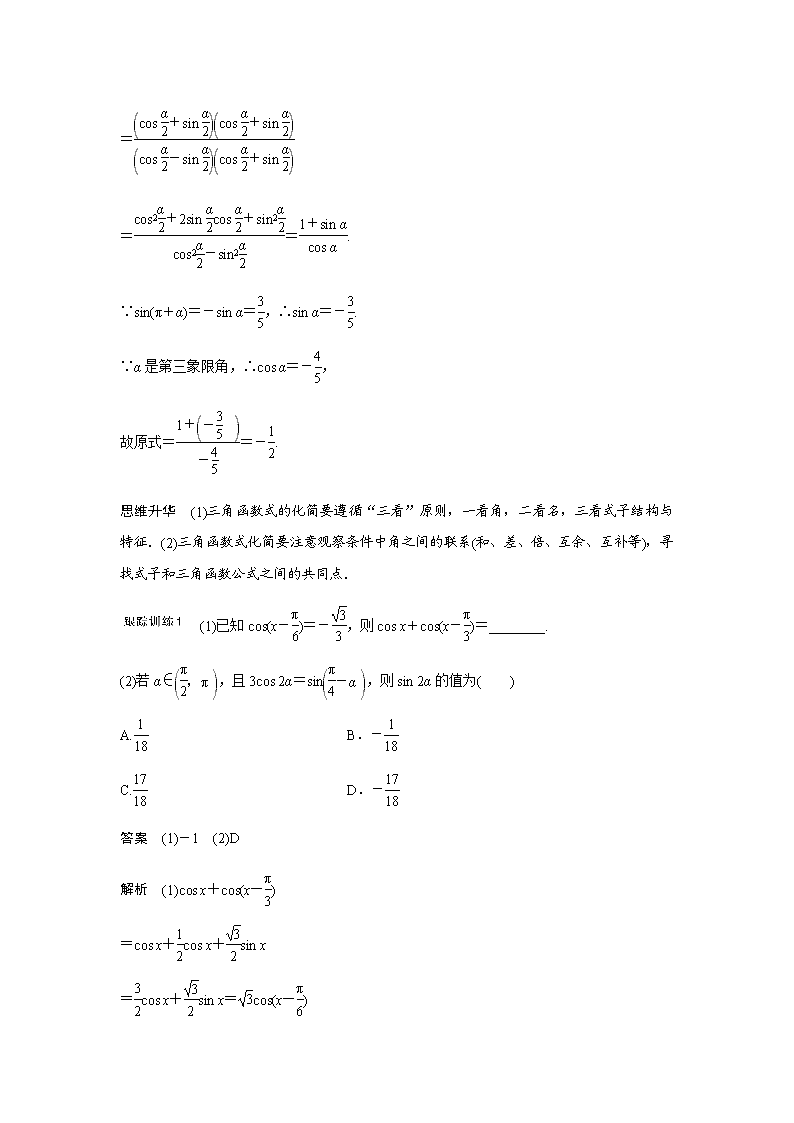2018版高考数学(浙江·文理通用)大一轮教师文档讲义:第四章4-5第2课时简单的三角恒等变换
第2课时 简单的三角恒等变换
题型一 三角函数式的化简
例1 (1)化简:=________.
(2)(2017·嘉兴第一中学调研)若sin(π+α)=,α是第三象限角,则等于( )
A. B.-
C.2 D.-2
答案 (1)cos 2x (2)B
解析 (1)原式=
=
=
==cos 2x.
(2)=
=
==.
∵sin(π+α)=-sin α=,∴sin α=-.
∵α是第三象限角,∴cos α=-,
故原式==-.
思维升华 (1)三角函数式的化简要遵循“三看”原则,一看角,二看名,三看式子结构与特征.(2)三角函数式化简要注意观察条件中角之间的联系(和、差、倍、互余、互补等),寻找式子和三角函数公式之间的共同点.
(1)已知cos(x-)=-,则cos x+cos(x-)=________.
(2)若α∈,且3cos 2α=sin,则sin 2α的值为( )
A. B.-
C. D.-
答案 (1)-1 (2)D
解析 (1)cos x+cos(x-)
=cos x+cos x+sin x
=cos x+sin x=cos(x-)
=×(-)=-1.
(2)cos 2α=sin
=sin
=2sincos
代入原式,得
6sincos=sin,
∵α∈,∴cos=,
∴sin 2α=cos
=2cos2-1=-.
题型二 三角函数的求值
命题点1 给值求值问题
例2 (1)(2016·合肥联考)已知α,β为锐角,cos α=,sin(α+β)=,则cos β=________.
答案
解析 ∵α为锐角,
∴sin α= =.
∵α,β∈(0,),∴0<α+β<π.
又∵sin(α+β)
,
∴cos(α+β)=-.
cos β=cos[(α+β)-α]
=cos(α+β)cos α+sin(α+β)sin α
=-×+×==.
(2)(2015·广东)已知tan α=2.
①求tan(α+)的值;
②求的值.
解 ①tan(α+)=
==-3.
②
=
===1.
命题点2 给值求角问题
例3 (1)设α,β为钝角,且sin α=,cos β=-,则α+β的值为( )
A. B.
C. D.或
(2)已知α,β∈(0,π),且tan(α-β)=,tan β=-,则2α-β的值为________.
答案 (1)C (2)-
解析 (1)∵α,β为钝角,sin α=,cos β=-,
∴cos α=-,sin β=,
∴cos(α+β)=cos αcos β-sin αsin β=>0.
又α+β∈(π,2π),∴α+β∈(,2π),
∴α+β=.
(2)∵tan α=tan[(α-β)+β]=
==>0,
∴0<α<.
又∵tan 2α===>0,
∴0<2α<,
∴tan(2α-β)=
==1.
∵tan β=-<0,
∴<β<π,-π<2α-β<0,
∴2α-β=-.
引申探究
本例(1)中,若α,β为锐角,sin α=,cos β=,则α+β=________.
答案
解析 ∵α,β为锐角,∴cos α=,sin β=,
∴cos(α+β)=cos αcos β-sin αsin β
=×-×=.
又0<α+β<π,∴α+β=.
思维升华 (1)给值求值问题的关键在“变角”,通过角之间的联系寻找转化方法;
(2)给值求角问题:先求角的某一三角函数值,再求角的范围确定角.
(1)已知sin α=,sin(α-β)=-,α,β均为锐角,则角β等于( )
A. B.
C. D.
(2)(2016·义乌检测)若sin 2α=,sin(β-α)=,且α∈[,π],β∈[π,],则α+β的值是( )
A. B.
C.或 D.
答案 (1)C (2)A
解析 (1)∵α、β均为锐角,∴-<α-β<.
又sin(α-β)=-,∴cos(α-β)=.
又sin α=,∴cos α=,
∴sin β=sin[α-(α-β)]
=sin αcos(α-β)-cos αsin(α-β)
=×-×(-)=.
∴β=.
(2)因为α∈[,π],sin 2α=>0,
所以2α∈[,π],
所以cos 2α=-且α∈[,],
又因为sin(β-α)=>0,β∈[π,],
所以β-α∈[,π],
所以cos(β-α)=-,
因此sin(α+β)=sin[(β-α)+2α]
=sin(β-α)cos 2α+cos(β-α)sin 2α
=×(-)+(-)×
=-,
cos(α+β)=cos[(β-α)+2α]
=cos(β-α)cos 2α-sin(β-α)sin 2α
=(-)×(-)-×=,
又α+β∈[,2π],所以α+β=,故选A.
题型三 三角恒等变换的应用
例4 (2016·天津)已知函数f(x)=4tan xsin·cos-.
(1)求f(x)的定义域与最小正周期;
(2)讨论f(x)在区间上的单调性.
解 (1)f(x)的定义域为{x|x≠+kπ,k∈Z}.
f(x)=4tan xcos xcos-
=4sin xcos-
=4sin x-
=2sin xcos x+2sin2x-
=sin 2x+(1-cos 2x)-
=sin 2x-cos 2x=2sin.
所以f(x)的最小正周期T==π.
(2)令z=2x-,则函数y=2sin z的单调递增区间是
,k∈Z.
由-+2kπ≤2x-≤+2kπ,k∈Z,
得-+kπ≤x≤+kπ,k∈Z.
设A=,B={x|-+kπ≤x≤+kπ,k∈Z},易知A∩B=.
所以当x∈时,f(x)在区间上单调递增,在区间上单调递减.
思维升华 三角恒等变换的应用策略
(1)进行三角恒等变换要抓住:变角、变函数名称、变结构,尤其是角之间的关系;注意公式的逆用和变形用.
(2)把形如y=asin x+bcos x化为y=sin(x+φ),可进一步研究函数的周期、单调性、最值与对称性.
(1)函数f(x)=sin(x+φ)-2sin φcos x的最大值为________.
(2)函数f(x)=sin(2x-)-2sin2x的最小正周期是________.
答案 (1)1 (2)π
解析 (1)因为f(x)=sin(x+φ)-2sin φcos x
=sin xcos φ-cos xsin φ=sin(x-φ),
-1≤sin(x-φ)≤1,所以f(x)的最大值为1.
(2)f(x)=sin 2x-cos 2x-(1-cos 2x)
=sin 2x+cos 2x-=sin(2x+)-,
∴T==π.
9.化归思想和整体代换思想在三角函数中的应用
典例 (15分)(2015·重庆)已知函数f(x)=sinsin x-cos2x.
(1)求f(x)的最小正周期和最大值;
(2)讨论f(x)在上的单调性.
思想方法指导 (1)讨论形如y=asin ωx+bcos ωx型函数的性质,一律化成y=sin(ωx+φ)型的函数.
(2)研究y=Asin(ωx+φ)型函数的最值、单调性,可将ωx+φ视为一个整体,换元后结合y=sin x的图象解决.
规范解答
解 (1)f(x)=sinsin x-cos2x
=cos xsin x-(1+cos 2x)=sin 2x-cos 2x-=sin-, [6分]
因此f(x)的最小正周期为π,最大值为.[7分]
(2)当x∈时,0≤2x-≤π, [9分]
从而当0≤2x-≤,
即≤x≤时,f(x)单调递增, [11分]
当≤2x-≤π,
即≤x≤时,f(x)单调递减. [13分]
综上可知,f(x)在上单调递增;在上单调递减. [15分]
1.(2016·宁波模拟)设tan(α-)=,则tan(α+)等于( )
A.-2 B.2 C.-4 D.4
答案 C
解析 因为tan(α-)==,
所以tan α=,故tan(α+)==-4,故选C.
2.(2016·全国甲卷)若cos=,则sin 2α等于( )
A. B. C.- D.-
答案 D
解析 因为sin 2α=cos=2cos2-1,又因为cos=,所以sin 2α=2×-1=-,故选D.
3.(2016·富阳模拟)已知tan α=3,则的值等于( )
A.2 B.3
C.4 D.6
答案 D
解析 ==2tan α=2×3=6.
4.已知tan(α+)=,且-<α<0,则等于( )
A.- B.-
C.- D.
答案 A
解析 由tan(α+)==,得tan α=-.
又-<α<0,所以sin α=-.
故==2sin α
=-.
5.设α∈(0,),β∈(0,),且tan α=,则( )
A.3α-β= B.2α-β=
C.3α+β= D.2α+β=
答案 B
解析 由tan α=,得=,
即sin αcos β=cos α+cos αsin β,
∴sin(α-β)=cos α=sin(-α).
∵α∈(0,),β∈(0,),
∴α-β∈(-,),-α∈(0,),
由sin(α-β)=sin(-α),得α-β=-α,
∴2α-β=.
6.函数f(x)=sin(2x+θ)+cos(2x+θ)的图象关于点对称,则f(x)的单调递增区间为( )
A.,k∈Z
B.,k∈Z
C.,k∈Z
D.,k∈Z
答案 C
解析 ∵f(x)=sin(2x+θ)+cos(2x+θ)
=2sin,
由题意知2×+θ+=kπ(k∈Z),
∴θ=kπ-π(k∈Z).
∵|θ|<,∴θ=.
∴f(x)=2sin.
由2kπ-≤2x+π≤2kπ+(k∈Z),
得kπ-π≤x≤kπ-(k∈Z).故选C.
7.(2016·宁波十校联考)已知函数f(x)=sin xcos x-cos2x-,x∈R,则函数f(x
)的最小值为________,函数f(x)的单调递增区间为__________________.
答案 -2 [kπ-,kπ+],k∈Z
解析 因为f(x)=sin 2x--=sin(2x-)-1,所以f(x)的最小值为-2.令2kπ-≤2x-≤2kπ+,k∈Z,解得f(x)的单调递增区间为[kπ-,kπ+],k∈Z.
8.若锐角α、β满足(1+tan α)(1+tan β)=4,则α+β=________.
答案
解析 由(1+tan α)(1+tan β)=4,
可得=,即tan(α+β)=.
又α+β∈(0,π),∴α+β=.
9.化简:=________.
答案 -4
解析 原式=
==
===-4.
10.函数f(x)=sin x-2sin2x (≤x≤)的最小值是________.
答案 -1
解析 f(x)=sin x-(1-cos x)
=2sin(x+)-1,
又≤x≤,∴≤x+≤,
∴f(x)min=2sin -1=-1.
11.(2016·温州第一次适应性测试)已知2sin αtan α=3,且0<α<π.
(1)求α的值;
(2)求函数f(x)=4cos xcos(x-α)在[0,]上的值域.
解 (1)由已知,得2sin2α=3cos α,
则2cos2α+3cos α-2=0,
所以cos α=或cos α=-2(舍去),
又因为0<α<π,所以α=.
(2)由(1),得f(x)=4cos xcos(x-)
=4cos x(cos x+sin x)
=2cos2x+2sin xcos x
=1+cos 2x+sin 2x
=1+2sin(2x+),
由0≤x≤,得≤2x+≤,
所以当x=0时,f(x)取得最小值f(0)=2,
当x=时,f(x)取得最大值f()=3,
所以函数f(x)在[0,]上的值域为[2,3].
*12.已知函数f(x)=sinsin(+).
(1)求函数f(x)在[-π,0]上的单调区间;
(2)已知角α满足α∈(0,),2f(2α)+4f(-2α)=1,求f(α)的值.
解 f(x)=sinsin(+)
=sincos=sin x.
(1)函数f(x)的单调递减区间为[-π,-],单调递增区间为[-,0].
(2)2f(2α)+4f(-2α)=1
⇒sin 2α+2sin(-2α)=1
⇒2sin αcos α+2(cos2α-sin2α)=1
⇒cos2α+2sin αcos α-3sin2α=0
⇒(cos α+3sin α)(cos α-sin α)=0.
∵α∈(0,),
∴cos α-sin α=0⇒tan α=1得α=,
∴f(α)=sin=.
*13.已知函数f(x)=2cos2ωx-1+2cos ωxsin ωx(0<ω<1),直线x=是f(x)图象的一条对称轴.
(1)试求ω的值;
(2)已知函数y=g(x)的图象是由y=f(x)图象上各点的横坐标伸长到原来的2倍,然后再向左平移个单位长度得到的,若g=,α∈,求sin α的值.
解 f(x)=2cos2ωx-1+2cos ωxsin ωx
=cos 2ωx+sin 2ωx
=2sin.
(1)由于直线x=是函数f(x)=2sin图象的一条对称轴,
∴sin=±1.
∴ω+=kπ+(k∈Z),
∴ω=k+(k∈Z).
又0<ω<1,∴-<k<.
又∵k∈Z,从而k=0,∴ω=.
(2)由(1)知f(x)=2sin,
由题意可得
g(x)=2sin,
即g(x)=2cos x.
∵g=2cos=,
∴cos=.
又α∈,
∴<α+<,
∴sin=.
∴sin α=sin
=sincos -cossin
=×-×=.