- 2021-04-17 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2017-2018学年内蒙古巴彦淖尔市第一中学高二12月月考数学试题(A卷)
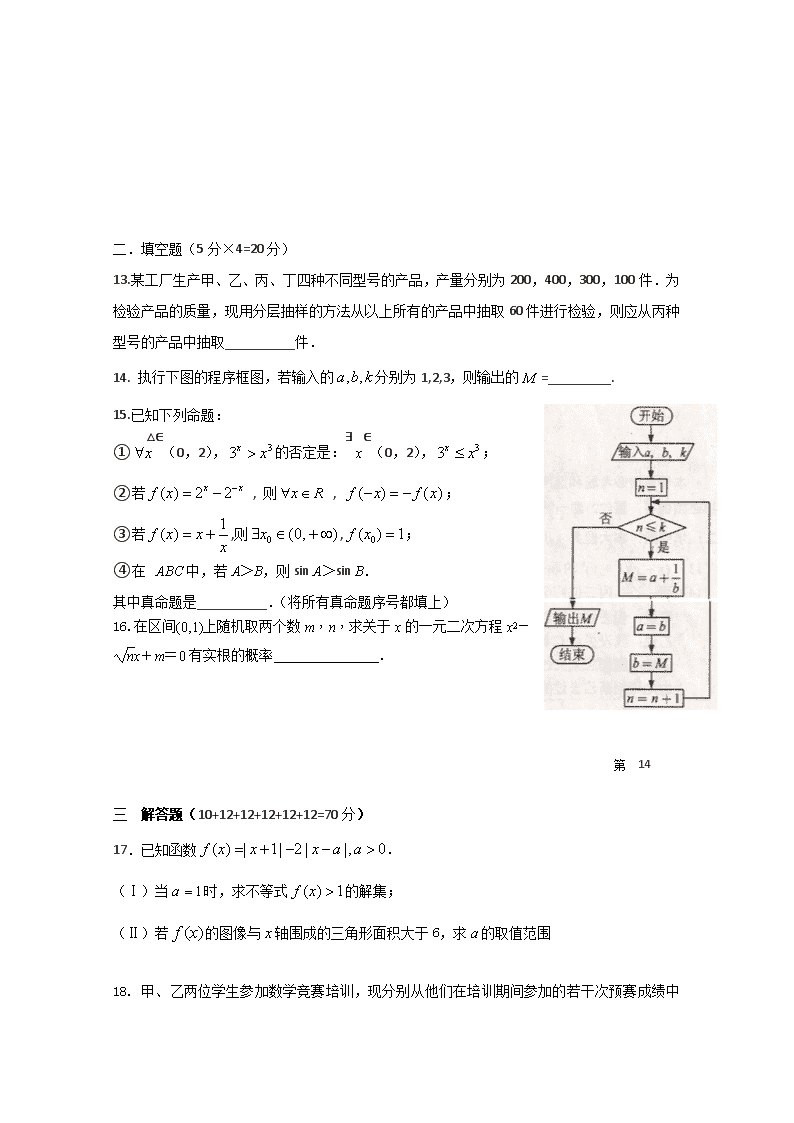
2017-2018学年内蒙古巴彦淖尔市第一中学高二12月月考数学试题A卷 命题人 王强 一.选择题(5分×12=60分)在每小题给出的四个选项只有一项正确. 1.已知变量之间具有线性相关关系,其散点图如图所示,则其回归方程可能为( ) A. B. C. D. 2.从装有2个红球和2个黑球的口袋内任取2个球,互斥而不对立的两个事件是( ) A.至少有一个黑球与都是黑球 B.至少有一个黑球与都是红球 C.至少有一个黑球与至少有1个红球 D.恰有1个黑球与恰有2个黑球 3.某中学教务处采用系统抽样方法,从学校高一年级全体1000名学生中抽50名学生做学习状况问卷调查.现将1000名学生从1到1000进行编号.在第一组中随机抽取一个号,如果抽到的是17号,则第8组中应取的号码是( ) A. 177 B. 417 C. 157 D. 367 4.下列有关命题的说法错误的是 ( ) A.命题“若,则”的逆否命题为:“若,则” B.“”是“”的必要不充分条件 C.若pq为假命题,则p、q均为假命题 D.对于命题p:∈R,使得,则∈R,均有≥0 5.已知命题使得命题,下列命题为真的是( ) A.( B.pq C. D. x 2 3 4 y 6 4 5 6.已知x,y的取值如表所示,如果y与x呈线性相关,且线性回归方程为,则b=( ) A. B. C. D. 7.如图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据(单位:件).若这两组数据的中位数相等,且平均值也相等,则x和y的值分别为( ) A. 3,5 B. 5,5 C. 3,7 D. 5,7 8. 设 ,则“ ”是“ ”的( ) A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件 9.在长为10cm的线段AB上任取一点C,现作一矩形,邻边长分别等于线段AC、CB的长,则该矩形面积小于24cm2的概率为( ) A. B. C. D. 10.若实数x+y+z=1,则2x2+y2+3z2 的最小值为( ) A. 1 B. C. D. 11 11. 不等式组的解集记为.有下面四个命题: :,:, :,:. 其中真命题是( ) ., ., ., ., 12.已知函数设,若关于的不等式在上恒成立,则的取值范围是( ) A. B. C. D. 二.填空题(5分×4=20分) 13.某工厂生产甲、乙、丙、丁四种不同型号的产品,产量分别为200,400,300,100件.为检验产品的质量,现用分层抽样的方法从以上所有的产品中抽取60件进行检验,则应从丙种型号的产品中抽取__________件. 14. 执行下图的程序框图,若输入的分别为1,2,3,则输出的=_________. 15.已知下列命题: ①∈(0,2),的否定是:∃ x∈(0,2),; ②若 , 则 , ; ③若,则,; ④在△ABC中,若A>B,则sin A>sin B. 其中真命题是__________.(将所有真命题序号都填上) 16.在区间(0,1)上随机取两个数m,n,求关于x的一元二次方程x2-x+m=0有实根的概率 . 第14题 三 解答题(10+12+12+12+12+12=70分) 17.已知函数. (Ⅰ)当时,求不等式的解集; (Ⅱ)若的图像与轴围成的三角形面积大于6,求的取值范围 18. 甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:] 甲 82 81 79 78 95 88 93 84 乙 92 95 80 75 83 80 90 85 (Ⅰ)用茎叶图表示这两组数据; (Ⅱ)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?请说明理由. 19. 一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4. (Ⅰ)从袋中随机取出两个球,求取出的球的编号之和不大于4的概率; (Ⅱ)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n<m+2的概率. 20. 命题p:关于x的不等式,对一切恒成立; 命题q:指数函数是增函数.若p或q为真,p且q为假,求实数a的取值范围. 21. 某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表。 B地区用户满意度评分的频数分布表 A地区用户满意度评分的频率分布直方图 (Ⅰ)在答题卡上作出B地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可); (Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个等级: 满意度评分 低于70分 70分到89分 不低于90分 满意度等级 不满意 满意 非常满意 估计哪个地区的满意度等级为不满意的概率大?说明理由 22. 近几年,京津冀等地数城市指数“爆表”,尤其2015年污染最重.为了探究车流量与PM2.5的浓度是否相关,现采集到北方某城市2015年12月份某星期星期一到星期日某一时间段车流量与PM2.5的数据如表: 时间 星期一 星期二 星期三 星期四 星期五 星期六 星期日 车流量x(万辆) 1 2 3[] 4 5 6 7[] PM2.5的浓度y(微克/立方米) 28 30 35 41 49 56 62 (Ⅰ)由散点图知y与x具有线性相关关系,求y关于x的线性回归方程; (Ⅱ)(ⅰ)利用(Ⅰ)所求的回归方程,预测该市车流量为8万辆时PM2.5的浓度; (ⅱ)规定:当一天内PM2.5的浓度平均值在(0,50]内,空气质量等级为优;当一天内PM2.5的浓度平均值在(50,100]内,空气质量等级为良.为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数.) 参考公式:回归直线的方程是,其中, . 巴彦淖尔市第一中学2017-2018学年第一学期 12月月考高二数学试题A卷参考答案 一、选择题 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 B D C B B A A A D C C A 二、填空题 (13)18 (14) (15) ①②④ (16) 三、解答题 17. (Ⅰ)当时,化为 当时,不等式化为,无解;[] 当时,不等式化为,解得; 当时,不等式化为,解得 所以的解集为 (Ⅱ)由题设可得, 所以函数的图像与轴围成的三角形的三个顶点分别为,,,的面积为 由题设得,故所以的取值范围为 18.解:(Ⅰ)作出茎叶图如下: (Ⅱ)派甲参赛比较合适,理由如下: 甲=(70×2+80×4+90×2+8+9+1+2+4+8+3+5)=85 乙=(70×1+80×4+90×3+5+0+0+3+5+0+2+5)=85. S=[(78-85)2+(79-85)2+(81-85)2+(82-85)2+(84-85)2+(88-85)2+(93-85)2+(95-85)2]=35.5 S=[(75-85)2+(80-85)2+(80-85)2+(83-85)2+(85-85)2+(90-85)2+(92-85)2 +(95-85)2]=41 ∵甲=乙,S查看更多
相关文章
- 当前文档收益归属上传用户
- 下载本文档