2020九年级数学上册反比例函数的图象和性质

2020九年级数学上册反比例函数的图象和性质

‎21.5 第2课时　反比例函数的图象和性质　　　　　　　　　　　　　　　‎ 知识点 1　反比例函数的图象 ‎1．下列说法错误的是(　　)‎ A．反比例函数的图象是双曲线 B．画反比例函数的图象时，注意用平滑的曲线分别顺次连接各象限内的各个点 C．反比例函数的图象与坐标轴没有交点 D．反比例函数的图象经过原点 ‎2．反比例函数y＝－的图象大致为(　　)‎ 图21－5－2‎ ‎3．［2017·无锡改编］若反比例函数y＝的图象经过点(－1，－2)，则该反比例函数的图象在(　　)‎ A．第一、二象限 B．第三、四象限 C．第一、三象限 D．第二、四象限 ‎4．下列各点中，在反比例函数y＝的图象上的是(　　)‎ A．(－1，4) B．(1，－4) ‎ C．(1，4) D．(2，3)‎ 知识点 2　反比例函数的性质 ‎5．下列函数中，y的值随x值的增大而减小的是(　　)‎ A．y＝－ B．y＝ C．y＝－(x>0) D．y＝(x<0)‎ ‎6．若反比例函数y＝的图象位于第二、四象限，则k的取值可以是(　　)‎ A．0 B．‎1 C．2 D．以上都不是 ‎7．［2017·赤峰］点A(1，y1)，B(3，y2)在反比例函数y＝的图象上，则y1，y2的大小关系是(　　)‎ A．y1＞y2 B．y1＝y2‎ C．y1＜y2 D．不能确定 ‎8．若A(x1，y1)，B(x2，y2)，C(x3，y3)是反比例函数y＝图象上的点，且x1y1>y2 B．y1>y2>y3‎ C．y2>y1>y3 D．y3>y2>y1‎ 7‎ ‎9．［教材练习第1题(2)变式］如果反比例函数y＝的图象经过点(－2，)，那么当x＞0时，y的值随x值的增大而________；当x＜0时，y的值随x值的增大而________．(填“增大”或“减小”)‎ ‎10．［教材例3变式］已知反比例函数y＝.‎ ‎(1)如果这个反比例函数图象与直线y＝－x交于点(a，5)，求出a和k的值，并直接写出它们另一个交点的坐标；‎ ‎(2)如果反比例函数y＝中，当x＜0时，y的值随x值的增大而增大，求k的取值范围．‎ ‎ ‎ 知识点 3　反比例函数y＝中k的几何意义 ‎11．如图21－5－3，点B在反比例函数y＝(x>0)的图象上，且横坐标为1.过点B分别向x轴、y轴作垂线，垂足分别为A，C，则矩形OABC的面积为(　　)‎ A．1 　B．‎2 C．3 D．4‎ 图21－5－3‎ ‎12．［2017·永州］如图21－5－4，已知反比例函数y＝的图象经过点A，过点A作AB⊥x轴，垂足为B.若△AOB的面积为1，则k＝________．‎ 图21－5－4‎ ‎13．如图21－5－5，A，B两点在反比例函数y＝(x>0)的图象上，分别经过A，B 7‎ 两点向坐标轴作垂线段，已知S阴影＝1，则S1＋S2等于(　　)‎ A．3　　　 B．‎4　　‎　 C．5　　　 D．6‎ 图21－5－5‎ ‎14．已知反比例函数y＝的图象如图21－5－6所示，则二次函数y＝2kx2－4x－2k的图象大致为(　　)‎ ‎　　　‎ 图21－5－6‎ 图21－5－7‎ ‎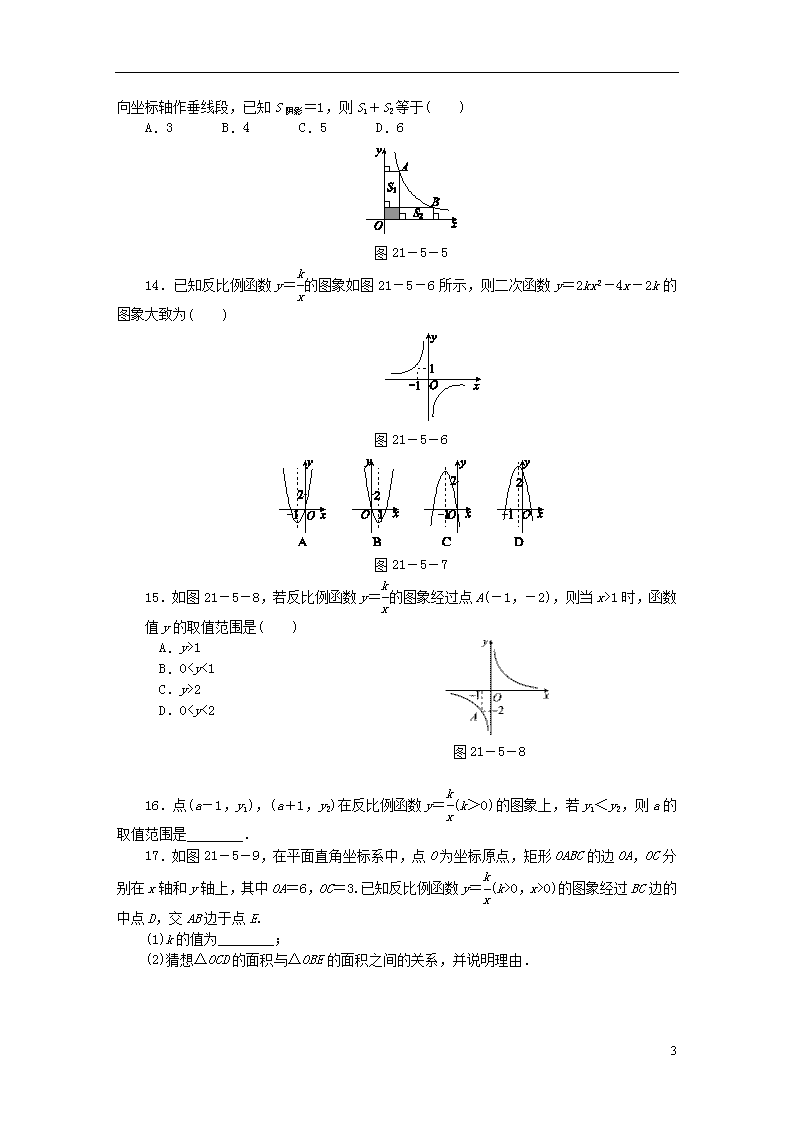15．如图21－5－8，若反比例函数y＝的图象经过点A(－1，－2)，则当x>1时，函数 值y的取值范围是(　　)‎ A．y>1‎ B．02‎ D．00，x>0)的图象经过BC边的中点D，交AB边于点E.‎ ‎(1)k的值为________；‎ ‎(2)猜想△OCD的面积与△OBE的面积之间的关系，并说明理由．‎ 7‎ 图21－5－9‎ ‎18．如图21－5－10，已知点A1，A2，…，An均在直线y＝x－1上，点B1，B2，…，Bn均在双曲线y＝－上，并且满足： A1B1⊥x轴，B‎1A2⊥y轴，A2B2⊥x轴，B‎2A3⊥y轴，…，AnBn⊥x轴，BnAn＋1⊥y轴，…，记点An的横坐标为an(n为正整数)．若a1＝－1， 则a2018＝________．‎ 图21－5－10‎ ‎19．如图21－5－11，点A(m，6)，B(n，1)在某反比例函数的图象上，AD⊥x轴于点D，BC⊥x轴于点C，DC＝5.‎ ‎(1)求m，n的值，并写出反比例函数的表达式；‎ ‎(2)连接AB，在线段DC上是否存在一点E，使△ABE的面积等于5？若存在，求出点E的坐标；若不存在，请说明理由．‎ 图21－5－11‎ 7‎ 教师详解详析 ‎1．D　2.D ‎3．C　[解析] 将点的坐标代入，可以求出k＝2，确定反比例函数的图象分布在第一、三象限．‎ ‎4．C　[解析] 根据y＝，得xy＝4，所以只要点的横坐标与纵坐标的积等于4，此点就在函数的图象上．选项A中－1×4＝－4≠4，故不在函数图象上；选项B中1×(－4)＝－4≠4，故不在函数图象上；选项C中1×4＝4，故在函数图象上；选项D中2×3＝6≠4，故不在函数图象上．故选C.‎ ‎5．D　[解析] 在反比例函数中，只有当系数k＞0，且在具体的象限中时，才有y的值随x值的增大而减小的情况．‎ ‎6．A　[解析] ∵反比例函数的图象位于第二、四象限，∴k－1＜0，即k＜1.故选A.‎ ‎7．A　[解析] 解法一：将x＝1和x＝3分别代入反比例函数表达式中，计算出y1，y2进行比较；解法二：∵k＝9＞0，∴函数图象位于第一、三象限，且在每个分支上，y随x的增大而减小．‎ ‎∵3＞1，∴y2＜y1.‎ ‎8．A　[解析] 因为k＝3>0，所以反比例函数的图象在第一、三象限，且在每一象限内y随x的增大而减小．因为x10)的图象上的点，分别经过A，B两点向x轴、y轴作垂线段，则根据反比例函数的图象的性质得两个矩形的面积都等于|k|＝4，∴S1＋S2＝4＋4－1×2＝6.‎ ‎14．D ‎[解析] 由反比例函数的图象知>1，即k<－1，则二次函数y＝2kx2－4x－2k的图象开口向下，对称轴为直线x＝－＝，在－1和0之间，故选D.‎ ‎15． D 7‎ ‎[解析] 先由图象经过点A，用待定系数法求得其表达式为y＝，又由反比例函数的性质，当x＞0时，y随x的增大而减小，故当x＞1时，0＜y＜2.故选D.‎ ‎16．[全品导学号：21002081]－1＜a＜1‎ ‎[解析] ∵k＞0，‎ ‎∴在图象的每一分支上，y随x的增大而减小．‎ ‎①当点(a－1，y1)，(a＋1，y2)在图象的同一分支上时，∵y1＜y2，∴a－1＞a＋1，无解；‎ ‎②当点(a－1，y1)，(a＋1，y2)在图象的两分支上时，‎ ‎∵y1＜y2，∴a－1＜0，a＋1＞0，‎ 解得－1＜a＜1.‎ ‎17．解：(1)由题意可得C(0，3)，B(6，3)，‎ 则BC边的中点D的坐标为(3，3)．‎ ‎∵反比例函数y＝(k>0，x>0)的图象经过点D，∴k＝9.‎ ‎(2)相等．理由如下：‎ 对于y＝，令x＝6，则y＝，‎ ‎∴E(6，)，即OA＝6，AE＝，‎ 从而BE＝AB－AE＝，‎ ‎∴S△OBE＝BE·OA＝××6＝.‎ 又∵S△OCD＝CD·OC＝×3×3＝，‎ ‎∴S△OBE＝S△OCD.‎ ‎18．2　[解析] ∵a1＝－1，‎ ‎∴B1的坐标是(－1，1)，‎ ‎∴A2的坐标是(2，1)，即a2＝2.‎ ‎∵a2＝2，‎ ‎∴B2的坐标是(2，－)，‎ ‎∴A3的坐标是(，－)，即a3＝.‎ ‎∵a3＝，‎ ‎∴B3的坐标是(，－2)，‎ ‎∴A4的坐标是(－1，－2)，即a4＝－1.‎ ‎∵a4＝－1，‎ ‎∴B4的坐标是(－1，1)，‎ ‎∴A5的坐标是(2，1)，即a5＝2.‎ ‎……‎ 7‎ ‎∴a1，a2，a3，a4，a5，…每3个数为一个循环，分别是－1，2，.‎ ‎∵2018÷3＝672……2，‎ ‎∴a2018是第673个循环中的第2个数，‎ ‎∴a2018＝2.‎ ‎19．解：(1)根据题意，得 解得 ‎∴m，n的值分别为1，6，即A(1，6)，B(6，1)．‎ 设反比例函数的表达式为y＝(k≠0)．‎ 将A(1，6)代入y＝，得k＝xy＝1×6＝6.‎ ‎∴反比例函数的表达式为y＝.‎ ‎(2)存在．‎ 如图，设E(x，0)，则DE＝x－1，CE＝6－x.‎ ‎∵AD⊥x轴，BC⊥x轴，‎ ‎∴∠ADE＝∠BCE＝90°.‎ 连接AE，BE.‎ S△ABE＝S梯形ABCD－S△ADE－S△BCE＝(BC＋AD)·DC－DE·AD－CE·BC＝×(1＋6)×5－(x－1)×6－(6－x)×1＝－x＝5，‎ 解得x＝5，‎ ‎∴点E的坐标为(5，0)．‎ 7‎