- 2021-02-26 发布 |
- 37.5 KB |
- 86页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
中考数学压轴题填空选择解答题分类汇编一及答案
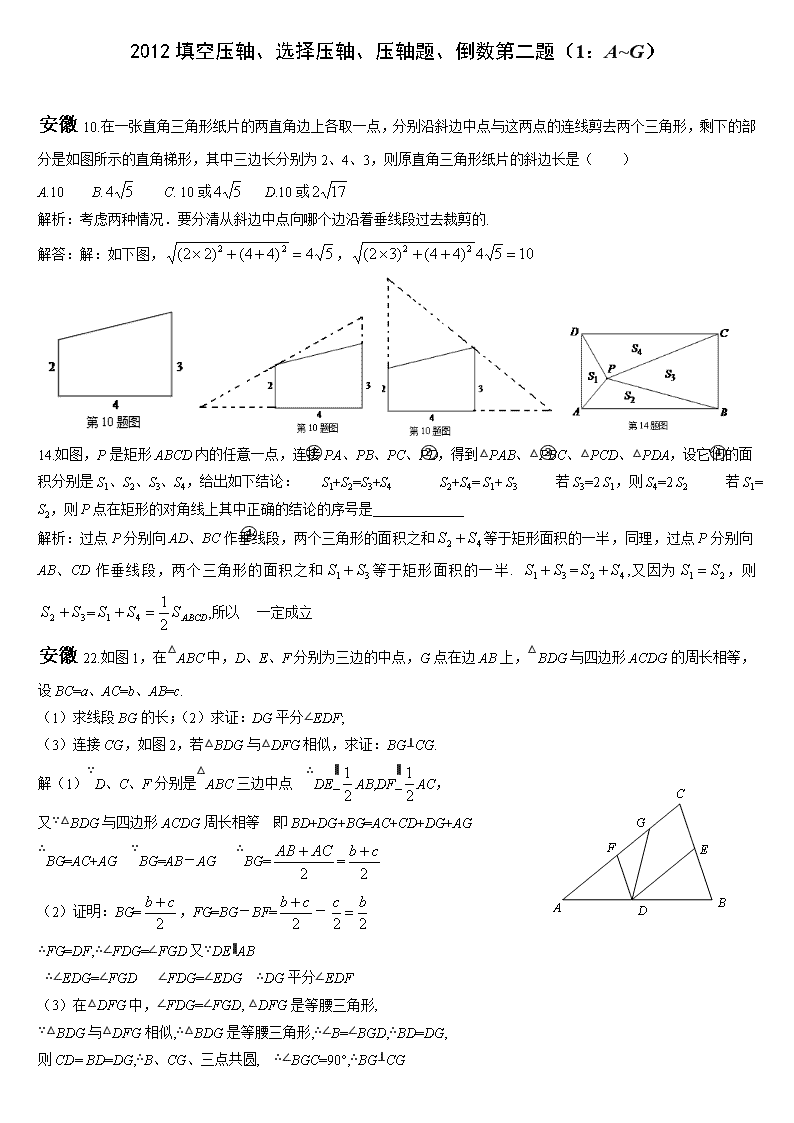
2012填空压轴、选择压轴、压轴题、倒数第二题(1:A~G) 安徽10.在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边长是( ) A.10 B. C. 10或 D.10或 解析:考虑两种情况.要分清从斜边中点向哪个边沿着垂线段过去裁剪的. 解答:解:如下图,, 14.如图,P是矩形ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4,给出如下结论: ①S1+S2=S3+S4 ② S2+S4= S1+ S3 ③若S3=2 S1,则S4=2 S2 ④若S1= S2,则P点在矩形的对角线上其中正确的结论的序号是_____________ 解析:过点P分别向AD、BC作垂线段,两个三角形的面积之和等于矩形面积的一半,同理,过点P分别向AB、CD作垂线段,两个三角形的面积之和等于矩形面积的一半. =,又因为,则=,所以④一定成立 安徽22.如图1,在△ABC中,D、E、F分别为三边的中点,G点在边AB上,△BDG与四边形ACDG的周长相等,设BC=a、AC=b、AB=c. (1)求线段BG的长;(2)求证:DG平分∠EDF; (3)连接CG,如图2,若△BDG与△DFG相似,求证:BG⊥CG. 解(1)∵D、C、F分别是△ABC三边中点 ∴DE∥AB,DF∥AC, 又∵△BDG与四边形ACDG周长相等 即BD+DG+BG=AC+CD+DG+AG ∴BG=AC+AG ∵BG=AB-AG ∴BG== (2)证明:BG=,FG=BG-BF=- ∴FG=DF,∴∠FDG=∠FGD又∵DE∥AB ∴∠EDG=∠FGD ∠FDG=∠EDG ∴DG平分∠EDF (3)在△DFG中,∠FDG=∠FGD, △DFG是等腰三角形, ∵△BDG与△DFG相似,∴△BDG是等腰三角形,∴∠B=∠BGD,∴BD=DG, 则CD= BD=DG,∴B、CG、三点共圆, ∴∠BGC=90°,∴BG⊥CG 23.如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m。 (1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围) (2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由; (3)若球一定能越过球网,又不出边界,求h的取值范围。 23解:(1)把x=0,y=2,及h=2.6代入到y=a(x-6)2+h 即2=a(0-6)2+2.6, ∴ ∴y= (x-6)2+2.6 (2)当h=2.6时,y= (x-6)2+2.6 x=9时,y= (9-6)2+2.6=2.45>2.43 ∴球能越过网 x=18时,y= (18-6)2+2.6=0.2>0 ∴球会过界 (3)x=0,y=2,代入到y=a(x-6)2+h得; x=9时,y= (9-6)2+h>2.43 ① x=18时,y= (18-6)2+h>0 ② 由① ②得h≥ 北京8. 小翔在如图1所示的场地上匀速跑步,他从点出发,沿箭头所示方向经过点跑到点,共用时30秒.他的教练选择了一个固定的位置观察小翔的跑步过程.设小翔跑步的时间为(单位:秒),他与教练的距离为(单位:米),表示与的函数关系的图象大致如图2所示,则这个固定位置可能是图1中的 A.点 B.点 C.点 D.点 【解析】 D 12.在平面直角坐标系中,我们把横 、纵坐标都是整数的点叫做整点.已知点,点是轴正半轴上的整点,记内部(不包括边界)的整点个数为.当时,点的横坐标的所有可能值是 ;当点的横坐标为(为正整数)时, (用含的代数式表示.) 【解析】 3或4; 北京24.在中,,是的中点,是线段上的动点,将线段绕点 顺时针旋转得到线段。 (1) 若且点与点重合(如图1),线段的延长线交射线于点,请补全图形,并写出的度数; (2) 在图2中,点不与点重合,线段的延长线与射线交于点,猜想的大小(用含的代数式表示),并加以证明; (3) 对于适当大小的,当点在线段上运动到某一位置(不与点,重合)时,能使得线段的延长线与射线交于点,且,请直接写出的范围。 【解析】 ⑴ , ⑵ 连接,易证 ∴ 又∵ ∴, ∴ ∴ ∴ ∴ ∴ ⑶ ∵且 ∴ ∵点不与点重合 ∴ ∴ ∴ 25.在平面直角坐标系中,对于任意两点与的“非常距离”,给出如下定义: 若,则点与点的“非常距离”为; 若,则点与点的“非常距离”为. 例如:点,点,因为,所以点与点的“非常距离”为,也就是图1中线段与线段长度的较大值(点为垂直于轴的直线与垂直于轴的直线的交点)。 (1)已知点,为轴上的一个动点, ①若点与点的“非常距离”为2,写出一个满足条件的点的坐标; ②直接写出点与点的“非常距离”的最小值; (2)已知是直线上的一个动点, ①如图2,点的坐标是(0,1),求点与点的“非常距离”的最小值及相应的点的坐标; ②如图3,是以原点为圆心,1为半径的圆上的一个动点,求点与点的“非常距离” 的最小值及相应的点和点的坐标。 【解析】⑴ ①或 ② ⑵ ①设坐标∴当此时∴距离为此时. ② ∴ ∴ 最小值1。 重庆10.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示对称轴为x=﹣.下列结论中,正确的是( ) A.abc>0 B.a+b=0 C.2b+c>0 D.4a+c<2b 解答: 解:A、∵开口向上,∴a>0,∵与y轴交与负半轴,∴c<0, ∵对称轴在y轴左侧,∴﹣<0,∴b>0,∴abc<0,故本选项错误; B、∵对称轴:x=﹣=﹣,∴a=b,故本选项错误;C、当x=1时,a+b+c=2b+c<0,故本选项错误; D、∵对称轴为x=﹣,与x轴的一个交点的取值范围为x1>1,∴与x轴的另一个交点的取值范围为x2<﹣2, ∴当x=﹣2时,4a﹣2b+c<0,即4a+c<2b,故本选项正确.故选D. 16.甲、乙两人玩纸牌游戏,从足够数量的纸牌中取牌.规定每人最多两种取法,甲每次取4张或(4﹣k)张,乙每次取6张或(6﹣k)张(k是常数,0<k<4).经统计,甲共取了15次,乙共取了17次,并且乙至少取了一次6张牌,最终两人所取牌的总张数恰好相等,那么纸牌最少有 108 张. 分析: 设甲a次取(4﹣k)张,乙b次取(6﹣k)张,则甲(15﹣a)次取4张,乙(17﹣b)次取6张,从而根据两人所取牌的总张数恰好相等,得出a、b之间的关系,再有取牌总数的表达式,讨论即可得出答案. 解答: 解:设甲a次取(4﹣k)张,乙b次取(6﹣k)张,则甲(15﹣a)次取4张,乙(17﹣b)次取6张, 则甲取牌(60﹣ka)张,乙取牌(102﹣kb)张,则总共取牌:N=a(4﹣k)+4(15﹣a)+b(6﹣k)+6(17﹣b)=﹣k(a+b)+162, 从而要使牌最少,则可使N最小,因为k为正数,函数为减函数,则可使(a+b)尽可能的大,由题意得,a≤15,b≤16, 又最终两人所取牌的总张数恰好相等,故k(b﹣a)=42,而0<k<4,b﹣a为整数, 则由整除的知识,可得k可为1,2,3, ①当k=1时,b﹣a=42,因为a≤15,b≤16,所以这种情况舍去; ②当k=2时,b﹣a=21,因为a≤15,b≤16,所以这种情况舍去; ③当k=3时,b﹣a=14,此时可以符合题意, 综上可得:要保证a≤15,b≤16,b﹣a=14,(a+b)值最大,则可使b=16,a=2;b=15,a=1;b=14,a=0; 当b=16,a=2时,a+b最大,a+b=18,继而可确定k=3,(a+b)=18,所以N=﹣3×18+162=108张. 故答案为:108. 重庆 企业的污水处理有两种方式,一种是输送到污水厂进行集中处理,另一种是通过企业的自身设备进行处理.某企业去年每月的污水量均为12000吨,由于污水厂处于调试阶段,污水处理能力有限,该企业投资自建设备处理污水,两种处理方式同时进行.1至6月,该企业向污水厂输送的污水量y1(吨)与月份x(1≤x≤6,且x取整数)之间满足的函数关系如下表: 7至12月,该企业自身处理的污水量y2(吨)与月份x(7≤x≤12,且x取整数)之间满足二次函数关系式为.其图象如图所示.1至6月,污水厂处理每吨污水的费用:(元)与月份x之间满足函数关系式:,该企业自身处理每吨污水的费用:(元)与月份x之间满足函数关系式:;7至12月,污水厂处理每吨污水的费用均为2元,该企业自身处理每吨污水的费用均为1.5元. (1)请观察题中的表格和图象,用所学过的一次函数、反比例函数或二次函数的有关知识,分别直接写出与x之间的函数关系式; (2)请你求出该企业去年哪个月用于污水处理的费用W(元)最多,并求出这个最多费用; (3)今年以来,由于自建污水处理设备的全面运行,该企业决定扩大产能并将所有污水全部自身处理,估计扩大产能后今年每月的污水量都将在去年每月的基础上增加a%,同时每吨污水处理的费用将在去年12月份的基础上增加(a﹣30)%,为鼓励节能降耗,减轻企业负担,财政对企业处理污水的费用进行50%的补助.若该企业每月的污水处理费用为18000元,请计算出a的整数值.(参考数据:≈15.2,≈20.5,≈28.4) 解答:解:(1)根据表格中数据可以得出xy=定值,则y1与x之间的函数关系为反比例函数关系:y1=,将(1,12000)代入得:k=1×12000=12000,故y1=(1≤x≤6,且x取整数); 根据图象可以得出:图象过(7, 10049),(12,10144)点,代入得:, 解得:,故y2=x2+10000(7≤x≤12,且x取整数); (2)当1≤x≤6,且x取整数时:W=y1x1+(12000﹣y1)•x2=•x+(12000﹣)•(x﹣x2), =﹣1000x2+10000x﹣3000,∵a=﹣1000<0,x=﹣=5,1≤x≤6,∴当x=5时,W最大=22000(元), 当7≤x≤12时,且x取整数时,W=2×(12000﹣y1)+1.5y2=2×(12000﹣x2﹣10000)+1.5(x2+10000),=﹣x2+1900, ∵a=﹣<0,x=﹣=0,当7≤x≤12时,W随x的增大而减小,∴当x=7时,W最大=18975.5(元),∵22000>18975.5, ∴去年5月用于污水处理的费用最多,最多费用是22000元; (3)由题意得:12000(1+a%)×1.5×[1+(a﹣30)%]×(1﹣50%)=18000,设t=a%,整理得:10t2+17t﹣13=0, 解得:t=,∵≈28.4,∴t1≈0.57,t2≈﹣2.27(舍去),∴a≈57, 答:a的值是57. 26.已知:如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=6,AB=3.E为BC边上一点,以BE为边作正方形BEFG,使正方形BEFG和梯形ABCD在BC的同侧. (1)当正方形的顶点F恰好落在对角线AC上时,求BE的长; (2)将(1)问中的正方形BEFG沿BC向右平移,记平移中的正方形BEFC为正方形B′EFG,当点E与点C重合时停止平移.设平移的距离为t,正方形B′EFG的边EF与AC交于点M,连接B′D,B′M,DM,是否存在这样的t,使△B′DM是直角三角形?若存在,求出t的值;若不存在,请说明理由; (3)在(2)问的平移过程中,设正方形B′EFG与△ADC重叠部分的面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围. 解答: 解:(1)如图①,设正方形BEFG的边长为x,则BE=FG=BG=x, ∵AB=3,BC=6,∴AG=AB﹣BG=3﹣x, ∵GF∥BE,∴△AGF∽△ABC,∴,即,解得:x=2,即BE=2; (2)存在满足条件的t, 理由:如图②,过点D作DH⊥BC于H,则BH=AD=2,DH=AB=3, 由题意得:BB′=HE=t,HB′=|t﹣2|,EC=4﹣t, 在Rt△B′ME中,B′M2=ME2+B′E2=22+(2﹣t)2=t2﹣2t+8, ∵EF∥AB,∴△MEC∽△ABC,∴,即,∴ME=2﹣t, 在Rt△DHB′中,B′D2=DH2+B′H2=32+(t﹣2)2=t2﹣4t+13,过点M作MN⊥DH于N, 则MN=HE=t,NH=ME=2﹣t,∴DN=DH﹣NH=3﹣(2﹣t)=t+1,在Rt△DMN中,DM2=DN2+MN2=t2+t+1, (Ⅰ)若∠DB′M=90°,则DM2=B′M2+B′D2,即t2+t+1=(t2﹣2t+8)+(t2﹣4t+13),解得:t=, (Ⅱ)若∠B′MD=90°,则B′D2=B′M2+DM2,即t2﹣4t+13=(t2﹣2t+8)+(t2+t+1), 解得:t1=﹣3+,t2=﹣3﹣(舍去),∴t=﹣3+; (Ⅲ)若∠B′DM=90°,则B′M2=B′D2+DM2,即:t2﹣2t+8=(t2﹣4t+13)+(t2+t+1),此方程无解, 综上所述,当t=或﹣3+时,△B′DM是直角三角形; (3)①如图③,当F在CD上时,EF:DH=CE:CH,即2:3=CE:4,∴CE=, ∴t=BB′=BC﹣B′E﹣EC=6﹣2﹣=,∵ME=2﹣t,∴FM=t,当0≤t≤时,S=S△FMN=×t×t=t2, ②当G在AC上时,t=2,∵EK=EC•tan∠DCB=EC•=(4﹣t)=3﹣t,∴FK=2﹣EK=t﹣1, ∵NL=AD=,∴FL=t﹣,∴当<t≤2时,S=S△FMN﹣S△FKL=t2﹣(t﹣)(t﹣1)=﹣t2+t﹣; ③如图⑤,当G在CD上时,B′C:CH=B′G:DH,即B′C:4=2:3,解得:B′C=, ∴EC=4﹣t=B′C﹣2=,∴t=,∵B′N=B′C=(6﹣t)=3﹣t,∵GN=GB′﹣B′N=t﹣1, ∴当2<t≤时,S=S梯形GNMF﹣S△FKL=×2×(t﹣1+t)﹣(t﹣)(t﹣1)=﹣t2+2t﹣, ④如图⑥,当<t≤4时,∵B′L=B′C=(6﹣t),EK=EC=(4﹣t),B′N=B′C=(6﹣t)EM=EC=(4﹣t), S=S梯形MNLK=S梯形B′EKL﹣S梯形B′EMN=﹣t+.综上所述: 当0≤t≤时,S=t2,当<t≤2时,S=﹣t2+t﹣;当2<t≤时,S=﹣t2+2t﹣,当<t≤4时,S=﹣t+. 福建福州10.如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+6于A、B两点,若反比例函数y=(x>0)的图像与△ABC有公共点,则k的取值范围是 A.2≤k≤9 B.2≤k≤8 C.2≤k≤5 D.5≤k≤8 解答:解:∵ 点C(1,2),BC∥y轴,AC∥x轴,∴ 当x=1时,y=-1+6=5, 当y=2时,-x+6=2,解得x=4,∴ 点A、B的坐标分别为A(4,2),B(1,5), 根据反比例函数系数的几何意义,当反比例函数与点C相交时,k=1×2=2最小, 设与线段AB相交于点(x,-x+6)时k值最大,则k=x(-x+6)=-x2+6x=-(x-3)2+9, ∵ 1≤x≤4,∴ 当x=3时,k值最大,此时交点坐标为(3,3),因此,k的取值范围是2≤k≤9. 故选A. 15.如图,已知△ABC,AB=AC=1,∠A=36°,∠ABC的平分线BD交AC于点D,则AD的长是______,cosA的值是______________.(结果保留根号) A B C D E 解答:∵ △ABC,AB=AC=1,∠A=36°,∴ ∠ABC=∠ACB==72°. ∵ BD是∠ABC的平分线,∴ ∠ABD=∠DBC=∠ABC=36°.∴ ∠A=∠DBC=36°, 又∵ ∠C=∠C,∴ △ABC∽△BDC,∴ =, 设AD=x,则BD=BC=x.则=,解得:x=(舍去)或.故x= . 如右图,过点D作DE⊥AB于点E,∵ AD=BD, ∴E为AB中点,即AE=AB=.在Rt△AED中,cosA===. 故答案是:;. 福建福州21.如图①,在Rt△ABC中,∠C=90º,AC=6,BC=8,动点P从点A开始沿边AC向点C以每秒1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ.点P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0). (1) 直接用含t的代数式分别表示:QB=______,PD=______. (2) 是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变点Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度; (3) 如图②,在整个运动过程中,求出线段PQ中点M所经过的路径长. 解答:解:(1) QB=8-2t,PD=t. 第21题图① A B C D P Q 第21题图② A B C D P Q A B C M1 x y P N Q M2 M3 D 图2 A B C P N Q D 图3 E M F H (2) 不存在. 在Rt△ABC中,∠C=90°,AC=6,BC=8,∴ AB=10. ∵ PD∥BC,∴ △APD∽△ACB, ∴ =,即:=,∴ AD=t,∴ BD=AB-AD=10-t. ∵ BQ∥DP,∴ 当BQ=DP时,四边形PDBQ是平行四边形,即8-2t=t,解得:t=. 当t=时,PD=×=,BD=10-×=6,∴ DP≠BD,∴ □PDBQ不能为菱形. 设点Q的速度为每秒v个单位长度, 则BQ=8-vt,PD=t,BD=10-t. 要使四边形PDBQ为菱形,则PD=BD=BQ, 当PD=BD时,即t=10-t,解得:t=. 当PD=BQ时,t=时,即×=8-v,解得:v=. (3) 解法一:如图2,以C为原点,以AC所在直线为x轴,建立平面直角坐标系. 依题意,可知0≤t≤4,当t=0时,点M1的坐标为(3,0); 当t=4时,点M2的坐标为(1,4).设直线M1M2的解析式为y=kx+b, ∴ ,解得:.∴ 直线M1M2的解析式为y=-2x+6. ∵ 点Q(0,2t),P(6-t,0), ∴ 在运动过程中,线段PQ中点M3的坐标为(,t). 把x=,代入y=-2x+6,得y=-2×+6=t.∴ 点M3在直线M1M2上. 过点M2作M2N⊥x轴于点N,则M2N=4,M1N=2.∴ M1M2=2. ∴ 线段PQ中点M所经过的路径长为2单位长度. 解法二:如图3,设E是AC的中点,连接ME. 当t=4时,点Q与点B重合,运动停止.设此时PQ的中点为F,连接EF. 过点M作MN⊥AC,垂足为N,则MN∥BC.∴ △PMN∽△PDC. ∴ ==,即:==.∴ MN=t,PN=3-t,∴ CN=PC-PN=(6-t)-(3-t)=3-t. ∴ EN=CE-CN=3-(3-t)= t.∴ tan∠MEN==2. ∵ tan∠MEN的值不变,∴ 点M在直线EF上. 过F作FH⊥AC,垂足为H.则EH=2,FH=4.∴ EF=2. ∵ 当t=0时,点M与点E重合;当t=4时,点M与点F重合,∴ 线段PQ中点M所经过的路径长为2单位长度. 22.如图①,已知抛物线y=ax2+bx(a≠0)经过A(3,0)、B(4,4)两点. (1) 求抛物线的解析式; (2) 将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个公共点D,求m的值及点D的坐标; (3) 如图②,若点N在抛物线上,且∠NBO=∠ABO,则在(2)的条件下,求出所有满足△POD∽△NOB的点P的坐标(点P、O、D分别与点N、O、B对应). 解:(1) ∵ 抛物线y=ax2+bx(a≠0)经过点A(3,0)、B(4,4). ∴ ,解得:.∴ 抛物线的解析式是y=x2-3x. D A B O x y N 图1 A' P1 N1 P2 B1 图2 A' N2 P1 P2 B2 A B D O x y N (2) 设直线OB的解析式为y=k1x,由点B(4,4),得:4=4k1,解得k1=1.∴ 直线OB的解析式为y=x. ∴ 直线OB向下平移m个单位长度后的解析式为:y=x-m. ∵ 点D在抛物线y=x2-3x上.∴ 可设D(x,x2-3x).又点D在直线y=x-m上, ∴ x2-3x =x-m,即x2-4x+m=0. ∵ 抛物线与直线只有一个公共点,∴ △=16-4m=0,解得:m=4. 此时x1=x2=2,y=x2-3x=-2,∴ D点坐标为(2,-2). (3) ∵ 直线OB的解析式为y=x,且A(3,0),∴ 点A关于直线OB的对称点A'的坐标是(0,3). 设直线A'B的解析式为y=k2x+3,过点B(4,4),∴ 4k2+3=4,解得:k2=. ∴ 直线A'B的解析式是y=x+3. ∵ ∠NBO=∠ABO,∴ 点N在直线A'B上,∴ 设点N(n,n+3),又点N在抛物线y=x2-3x上, ∴ n+3=n2-3n, 解得:n1=-,n2=4(不合题意,会去),∴ 点N的坐标为(-,). 方法一:如图1,将△NOB沿x轴翻折,得到△N1OB1,则N1(-,-),B1(4,-4), ∴ O、D、B1都在直线y=-x上. ∵ △P1OD∽△NOB,∴ △P1OD∽△N1OB1,∴ ==,∴ 点P1的坐标为(-,-). 将△OP1D沿直线y=-x翻折,可得另一个满足条件的点P2(,). 综上所述,点P的坐标是(-,-)或(,). 方法二:如图2,将△NOB绕原点顺时针旋转90°,得到△N2OB2,则N2(,),B2(4,-4), ∴ O、D、B2都在直线y=-x上. ∵ △P1OD∽△NOB,∴ △P1OD∽△N2OB2,∴ ==,∴ 点P1的坐标为(,). 将△OP1D沿直线y=-x翻折,可得另一个满足条件的点P2(-,-). 综上所述,点P的坐标是(-,-)或(,). 福建龙岩10.如图,矩形ABCD中,AB=1,BC=2,把矩形ABCD 绕AB所在直线旋转一周所得圆柱的侧面积为 A. B. C. D.2 B (第10题图) (第17题图) 17.如图,平面直角坐标系中,⊙O1过原点O,且⊙O1与⊙O2相外切,圆心O1与O2在x轴正半轴上,⊙O1的半径O1P1、⊙O2的半径O2P2都与x轴垂直,且点P1、P2在反比例函数(x>0)的图象上,则_________. 福建龙岩24.矩形ABCD中,AD=5,AB=3,将矩形ABCD沿某直线折叠,使点A的对应点A′落在线段BC上,再打开得到折痕EF. (1)当A′与B重合时(如图1),EF= ;当折痕EF过点D时(如图2),求线段EF的长; (2)观察图3和图4,设BA′=x,①当x的取值范围是 时,四边形AEA′F是菱形;②在①的条件下,利用图4证明四边形AEA′F是菱形. 24. (1) 5 ……………………………………………………2分 解法1:由折叠(轴对称)性质知 ° 在Rt△中,=3 ∴ ∴ ∵ ∵ 又 ∵° ∴Rt△∽Rt△ ∴ 在Rt△中,…6分 解法2:同解法1得设,则 ………4分 在Rt△中, ∴ 在Rt△中,……6分 解法3:同解法1得Rt△∽Rt△ ∴=15-6- 连结, =∴ (2)① ②证明: 法一:由折叠(轴对称)性质知 又 ∵∥BC ∴∠AFE=∠FEA′ ∴∠AEF=∠AFE ∴AE=AF ∴ ∴四边形是菱形. 法二:由折叠(轴对称)性质知,, 过作,交AD于G,证明得 ∴ ∴四边形是菱形 25.在平面直角坐标系xoy中, 一块含60°角的三角板作如图摆放,斜边 AB在x轴上,直角顶点C在y轴正半轴上,已知点A(-1,0). (1)请直接写出点B、C的坐标:B( , )、C( , );并求经过A、B、C三点的抛物线解析式; (2)现有与上述三角板完全一样的三角板DEF(其中∠EDF=90°,∠DEF=60°),把顶点E放在线段AB上(点E是不与A、B两点重合的动点),并使ED所在直线经过点C. 此时,EF 所在直线与(1)中的抛物线交于第一象限的点M. ①设AE=x,当x为何值时,△OCE∽△OBC; ②在①的条件下探究:抛物线的对称轴上是否存在点P使△PEM是等腰三角形,若存在,请求出点P的坐标;若不存在,请说明理由. 备用图 25.(1)B(3,0),C(0,) 解:法1: 设过A、B、C三点的抛物线为,则 ∵A(—1,0)B(3,0) ∴ 又∵C(0,)在抛物线上 ∴ ∴∴ 即 (2)①解:当△OCE∽△OBC时,则 ∵, OE=AE—AO=, OB=3 ∴ ∴ ∴当时,△OCE∽△OBC. (2)②解:存在点P. 理由如下: 由①可知 ∴OE=1 ∴E(1,0) 此时,△CAE为等边三角形 ∴∠AEC=∠A=60° 又∵∠CEM=60° ∴∠MEB=60° ∴点C与点M关于抛物线的对称轴对称. ∵C(0,) ∴M 过M作MN⊥轴于点N(2,0) ∴MN= ∴ EN=1 ∴ EM= 若△PEM为等腰三角形,则: ⅰ)当EP=EM时, ∵EM=2,且点P在直线上 ∴P(1,2)或P(1,—2) ⅱ)当EM=PM时,点M在EP的垂直平分线上 ∴P(1,2) ⅲ)当PE=PM时,点P是线段EM的垂直平分线与直线的交点 ∴P(1,) ∴综上所述,存在P点坐标为(1,2)或(1,—2)或(1,)或(1,)时,△EPM 为等腰三角形. 福建南平 10. 如图,正方形纸片ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别和AE、AF折叠,点B、D恰好都将在点G处,已知BE=1,则EF的长为【 】 A. B. C. D.3 【分析】∵正方形纸片ABCD的边长为3,∴∠C=90°,BC=CD=3。根据折叠的性质得:EG=BE=1,GF=DF。 设DF=x,则EF=EG+GF=1+x,FC=DC-DF=3-x,EC=BC-BE=3-1=2。 在Rt△EFC中,EF2=EC2+FC2,即(x+1)2=22+(3-x)2,解得:。 ∴DF= ,EF=1+。故选B。 18.设[x)表示大于x的最小整数,如[3)=4,[-1.2)=-1,则下列结论中正确的是 ▲ .(填写所有正确结论的序号)①[0)=0;②[x)-x的最小值是0;③[x)-x的最大值是0;④存在实数x,使[x)-x=0.5成立. 【分析】根据题意[x)表示大于x的最小整数,结合各项进行判断即可得出答案: ①[0)=1,故结论错误;②[x)-x>0,但是取不到0,故结论错误; ③[x)-x≤1,即最大值为1,故结论错误;④存在实数x,使[x)-x=0.5成立,例如x=0.5时,故结论正确。 福建南平25.在平面直角坐标系中,矩形OABC如图所示放置,点A在x轴上,点B的坐标为(m,1)(m>0),将此矩形绕O点逆时针旋转90°,得到矩形OA′B′C′. (1)写出点A、A′、C′的坐标; (2)设过点A、A′、C′的抛物线解析式为y=ax2+bx+c,求此抛物线的解析式;(a、b、c可用含m的式子表示) (3)试探究:当m的值改变时,点B关于点O的对称点D是否可能落在(2)中的抛物线上?若能,求出此时m的值. 【答案】解:(1)∵四边形ABCD是矩形,点B的坐标为(m,1)(m>0),∴A(m,0),C(0,1)。 ∵矩形OA′B′C′由矩形OABC旋转90°而成,∴A′(0,m),C′(-1,0)。(2)设过点A、A′、C′的抛物线解析式为y=ax2+bx+c, ∵A(m,0),A′(0,m),C′(-1,0), ∴,解得。∴此抛物线的解析式为:y=-x2+(m-1)x+m。 (3)∵点B与点D关于原点对称,B(m,1),∴点D的坐标为:(-m,-1), 假设点D(-m,-1)在(2)中的抛物线上, ∴0=-(-m)2+(m-1)×(-m)+m=1,即2m2-2m+1=0, ∵△=(-2)2-4×2×2=-4<0,∴此方程无解。∴点D不在(2)中的抛物线上。 26.如图,在△ABC中,点D、E分别在边BC、AC上,连接AD、DE,且∠1=∠B=∠C. (1)由题设条件,请写出三个正确结论:(要求不再添加其他字母和辅助线,找结论过程中添加的字母和辅助线不能出现在结论中,不必证明)答:结论一: ;结论二: ;结论三: . (2)若∠B=45°,BC=2,当点D在BC上运动时(点D不与B、C重合), ①求CE的最大值;②若△ADE是等腰三角形,求此时BD的长. 【答案】解:(1)AB=AC;∠AED=∠ADC;△ADE∽△ACD。 (2)①∵∠B=∠C,∠B=45°,∴△ACB为等腰直角三角形。∴。 ∵∠1=∠C,∠DAE=∠CAD,∴△ADE∽△ACD。∴AD:AC=AE:AD,∴ 。 当AD最小时,AE最小,此时AD⊥BC,AD=BC=1。∴AE的最小值为 。∴CE的最大值= 。 ②当AD=AE时,∴∠1=∠AED=45°,∴∠DAE=90°。∴点D与B重合,不合题意舍去。 当EA=ED时,如图1,∴∠EAD=∠1=45°。∴AD平分∠BAC,∴AD垂直平分BC。∴BD=1。 当DA=DE时,如图2,∵△ADE∽△ACD,∴DA:AC=DE:DC。∴DC=CA=。∴BD=BC-DC=2-。 综上所述,当△ADE是等腰三角形时,BD的长的长为1或2-。 福建宁德 10.如图,在矩形ABCD中,AB=2,BC=3,点E、F、G、H分别在矩形ABCD的各边上,EF∥HG,EH∥FG,则四边形EFGH的周长是【 】 A. B. C.2 D.2 【答案】D。 18.如图,点M是反比例函数y=在第一象限内图象上的点,作MB⊥x轴于点B.过点M的第一条直线交y轴于点A1,交反比例函数图象于点C1,且A1C1=A1M,△A1C1B的面积记为S1;过点M的第二条直线交y轴于点A2,交反比例函数图象于点C2,且A2C2=A2M,△A2C2B的面积记为S2;过点M的第三条直线交y轴于点A3,交反比例函数图象于点C3,且A3C3=A3M,△A3C3B的面积记为S3;依次类推…;则S1+S2+S3+…+S8= ▲ . 【答案】。 25.某数学兴趣小组开展了一次活动,过程如下: 如图1,在等腰△ABC中,AB=AC,∠BAC=90º,小敏将一块三角板中含45º角的顶点放在点A处,从AB边开始绕点A顺时针旋转一个角,其中三角板斜边所在的直线交直线BC于点D,直角边所在的直线交直线BC于点E. (1)小敏在线段BC上取一点M,连接AM,旋转中发现:若AD平分∠MAB,则AE也平分∠MAC.请你证明小敏发现的结论; (2)当0º<≤45º时,小敏在旋转的过程中发现线段BD、CE、DE之间存在如下等量关系:BD2+CE2=DE2.同组的小颖和小亮随后想出了两种不同的方法进行解决: 小颖的方法:将△ABD沿AD所在的直线对折得到△ADF,连接EF(如图2); 小亮的方法:将△ABD绕点A逆时针旋转90º得到△ACG,连接EG(如图3). 请你从中任选一种方法进行证明; (3)小敏继续旋转三角板,在探究中得出:当45º<≤135º且≠90º时,等量关系BD2+CE2=DE2 仍然成立.现请你继续探究:当135º<<180º时(如图4),等量关系BD2+CE2=DE2是否仍然成立?若成立,给出证明:若不成立,说明理由. 【答案】解:(1)证明:∵∠BAC=90º,∠DAE=∠DAM+∠MAE=45º,∴∠BAD+∠EAC=45º。 又∵AD平分∠MAB,∴∠BAD=∠DAM。∴∠MAE=∠EAC。∴AE平分∠MAC。 (2)证明小颖的方法: ∵将△ABD沿AD所在的直线对折得到△ADF,∴AF=AB,∠AFD=∠B=45º,∠BAD=∠FAD。 又∵AC=AB,∴AF=AC。 由(1)知,∠FAE=∠CAE。 在△AEF和△AEC中,∵AF= AC,∠FAE=∠CAE,AE=AE, ∴△AEF≌△AEC(SAS)。∴CE=FE,∠AFE=∠C=45º。 ∴∠DFE=∠AFD +∠AFE=90º。 在Rt△OCE中,DE2+FE2=DE2,∴BD2+CE2=DE2。 (3)当135º<<180º时,等量关系BD2+CE2=DE2仍然成立。证明如下: 如图,按小颖的方法作图,设AB与EF相交于点G。 ∵将△ABD沿AD所在的直线对折得到△ADF,∴AF=AB,∠AFD=∠ABC=45º,∠BAD=∠FAD。 又∵AC=AB,∴AF=AC。 又∵∠CAE=900-∠BAE=900-(45º-∠BAD)=45º+∠BAD=45º+∠FAD=∠FAE。 在△AEF和△AEC中,∵AF= AC,∠FAE=∠CAE,AE=AE, ∴△AEF≌△AEC(SAS)。∴CE=FE,∠AFE=∠C=45º。 又∵在△AGF和△BGE中,∠ABC=∠AFE=45º,∠AGF=∠BGE,∴∠FAG=∠BEG。 又∵∠FDE+∠DEF=∠FDE+∠FAG=(∠ADB+∠DAB)=∠ABC=90º。∴∠DFE=90º。 在Rt△OCE中,DE2+FE2=DE2,∴BD2+CE2=DE2。 26.如图,矩形OBCD的边OD、OB分别在x轴正半轴和y轴负半轴上,且OD=10,OB=8.将矩形的边BC绕点B逆时针旋转,使点C恰好与x轴上的点A重合. (1)直接写出点A、B的坐标:A( , )、B( , ); (2)若抛物线y=-x2+bx+c经过点A、B,则这条抛物线的解析式是 ; (3)若点M是直线AB上方抛物线上的一个动点,作MN⊥x轴于点N.问是否存在点M,使△AMN与△ACD相似?若存在,求出点M的坐标;若不存在,说明理由; (4)当≤x≤7,在抛物线上存在点P,使△ABP的面积最大,求△ABP面积的最大值. 【答案】解:(1)(6,0),(0,-8)。 (2)。 (3)存在。 设M,则N(m,0)MN=,NA=6-m。 又DA=4,CD=8, ①若点M在点N上方,,则△AMN∽△ACD。 ∴,即,解得m=6或m=10。 与点M是直线AB上方抛物线上的一个动点不符。∴此时不存在点M,使△AMN与△ACD相似。 ②若点M在点N下方,,则△AMN∽△ACD。 ∴,即,解得m=-2或m=6。 与点M是直线AB上方抛物线上的一个动点不符。∴此时不存在点M,使△AMN与△ACD相似。 ③若点M在点N上方,,则△AMN∽△ACD。 ∴,即,方程无解。∴此时不存在点M,使△AMN与△ACD相似。 ④若点M在点N下方,,则△AMN∽△ACD。 ∴,即,解得m=或m=6。 当m=时符合条件。∴此时存在点M(,),使△AMN与△ACD相似。 综上所述,存在点M(,),使△AMN与△ACD相似。 (4)设P(p,), 在中,令y=0,得x=4或x=6。 ∴≤x≤7分为≤x<4,4≤x<6和6≤x≤7三个区间讨论: ①如图,当≤x<4时,过点P作PH⊥x轴于点H则OH=p,HA=6-p ,PH=。 ∴ ∴当≤x<4时,随p的增加而减小。 ∴当x=时,取得最大值,最大值为。 ②如图,当4≤x<6时,过点P作PH⊥BC于点H,过点A作AG⊥BC于点G。 则BH= p,HG=6-p,PH=, ∴ ∴当4≤x<6时,随p的增加而减小。∴当x=4时,取得最大值,最大值为8。 ③如图,当6≤x≤7时,过点P作PH⊥x轴于点H。则OH=p,HA= p-6,PH=。 ∴ ∴当6≤x≤7时,随p的增加而增加。∴当x=7时,取得最大值,最大值为7。 综上所述,当x=时,取得最大值,最大值为。 福建泉州 ⒎如图,点O是△ABC的内心,过点O作EF∥AB,与AC、BC分别交于点E、F,则( ) A .EF>AE+BF B. EF查看更多