- 2021-02-26 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
一年级下册数学教案 数学百花园 百数表 北京版 (10)
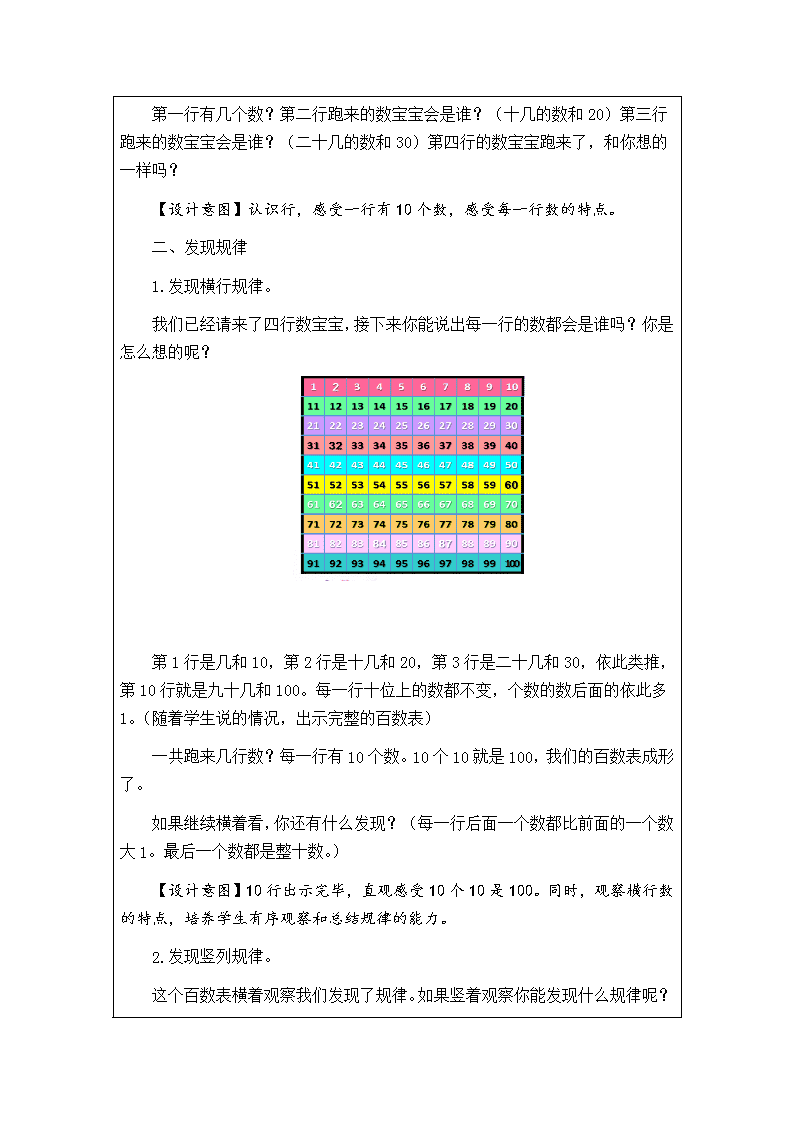
教学基本信息 课题 数学百花园——百数表 学科 数学 学段 第一学段 年级 一年级 相关 领域 数学 教材 北京版教材第二册 ⒈ 教学目标(含重、难点) 教学目标: 1. 通过观察百数表,探索并发现百数表中数的排列规律,感受数之间的关系。 2. 借助信息技术和百数表直观模型,引导学生运用行和列的对应关系确定具体的数,渗透坐标思想。 3. 通过数轴让学生体验数之间的顺序及位置关系,帮助学生逐步发展无限的观念。 教学重点:理解100以内数的排列规律。 教学难点:培养学生有序观察的能力和排列规律的应用。 ⒉ 教学过程 一、谈话引入 同学们,本学期我们学习了100以内数的认识,在学习数的顺序时,我们认识了百数表,还记得它吗?让我们把它再次请进我们的课堂。看,可爱的数宝宝排着整齐的队伍来了。 第一行有几个数?第二行跑来的数宝宝会是谁?(十几的数和20)第三行跑来的数宝宝会是谁?(二十几的数和30)第四行的数宝宝跑来了,和你想的一样吗? 【设计意图】认识行,感受一行有10个数,感受每一行数的特点。 二、发现规律 1.发现横行规律。 我们已经请来了四行数宝宝,接下来你能说出每一行的数都会是谁吗?你是怎么想的呢? 第1行是几和10,第2行是十几和20,第3行是二十几和30,依此类推,第10行就是九十几和100。每一行十位上的数都不变,个数的数后面的依此多1。(随着学生说的情况,出示完整的百数表) 一共跑来几行数?每一行有10个数。10个10就是100,我们的百数表成形了。 如果继续横着看,你还有什么发现?(每一行后面一个数都比前面的一个数大1。最后一个数都是整十数。) 【设计意图】10行出示完毕,直观感受10个10是100。同时,观察横行数的特点,培养学生有序观察和总结规律的能力。 2.发现竖列规律。 这个百数表横着观察我们发现了规律。如果竖着观察你能发现什么规律呢? 个位的数不变,十位依此增加1。(注意追问十位增加1其实是增加了10,结合百数表感受十位增加1,数就增加了10) 【设计意图】认识列,有序的观察列的规律。同时借助百数表直观的感受十位上的数字大1,这个数就大10,同时和位置相呼应。发现数的排列规律,渗透位值思想,深化学生对数位、计数单位的认识,感受数的神奇。 3.观察斜行规律。 数形结合,感受后面的数比前面的数多11,十位多1是多10,个位多1,合起来是多了11。 数形结合,感受后面的数比前面的数多9。 【设计意图】培养学生多角度探寻规律。同时利用百数表将两个数的关系直观的呈现出来,感受数与数之间的关系。 三、运用规律 1. 运用行与列填数。 随着观察的深入,我们越来越了解百数表了。快看,除了第一行和第一列,淘气的数宝宝们都藏起来了。你能找出它们吗? 教师随机说一个数,让孩子们到屏幕上指一指它的位置,并点开验证。 追问:你是怎么想的?(运用行与列相交来找到数的位置) 【设计意图】体会数与行、列的关系,掌握确定数在百数表中位置的方法,初步渗透位值思想、坐标思想,深化对数的认识。 2. 根据数之间的关系填数。 图中躲在红色方框后面的数宝宝是谁?这个数宝宝四个角上的数宝宝是谁呢?你是怎么找到的? 方法1:根据行、列来判断。 方法2:找到67上面的数是56,56左右两边各是55和57。67下面的数是77,77左右两边的数是76和78. 方法3: 67左上角的数比67小11,右下角的数比67大11,右上角的数比67大9,左下角的数比67小9。 【设计意图】学生运用多种方法确定数。深化对于坐标思想的认识,运用规律填写数,深化学生对于数与数之间的关系的理解。 3. 隐藏第一行和第一列分区域建立数之间的关系 (1)13在哪个颜色的区域?你是怎么想的? (2)89在哪个颜色的区域?你是怎么想的? (3)粉色区域的数宝宝和黄色色区域的数宝宝相比,谁大谁小?为什么? (4)你能想出每个区域最大的数宝宝和最小的数宝宝都是谁吗? 【设计意图】没有了行和列的提示,学生借助百数表的表象以及行和列之前的关系,运用多种策略和方法找到数的位置。 4. 利用数尺体验数之间的顺序及位置关系。 数宝宝们要排队进电影院了,这么多数宝宝,我们的屏幕都放不下了,我们把它们一队一队排开,绿色的队伍是哪个数宝宝到哪个数宝宝? 我们把所有的数宝宝都隐去了,你还都指导它们在哪里吗? 好了开始站队了。我们请第一行的数宝宝来站队,它们是谁到谁? (1)从10到20,从20到30,,从30到40……它们之间的长度一样吗?它们之间有几个数?(9个) (2)89这个数大约在什么位置?出示位置确定。 (3)大于60的数在哪儿?小于60的数在哪儿? (4)这个队伍最大的数是100,还有没有比100更大的数?它们会在哪里? 这个队伍最小的数是0,还有没有比0更小的数?它们会在哪里? 完善数轴: 【设计意图】把百数表变形成数尺,在数尺上进一步形象化地感受数之间的相对大小关系,感受数的无限,利用数尺渗透无限思想。查看更多