- 2021-02-26 发布 |
- 37.5 KB |
- 3页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
九年级下册数学教案 1-1 第2课时 正弦与余弦 北师大版
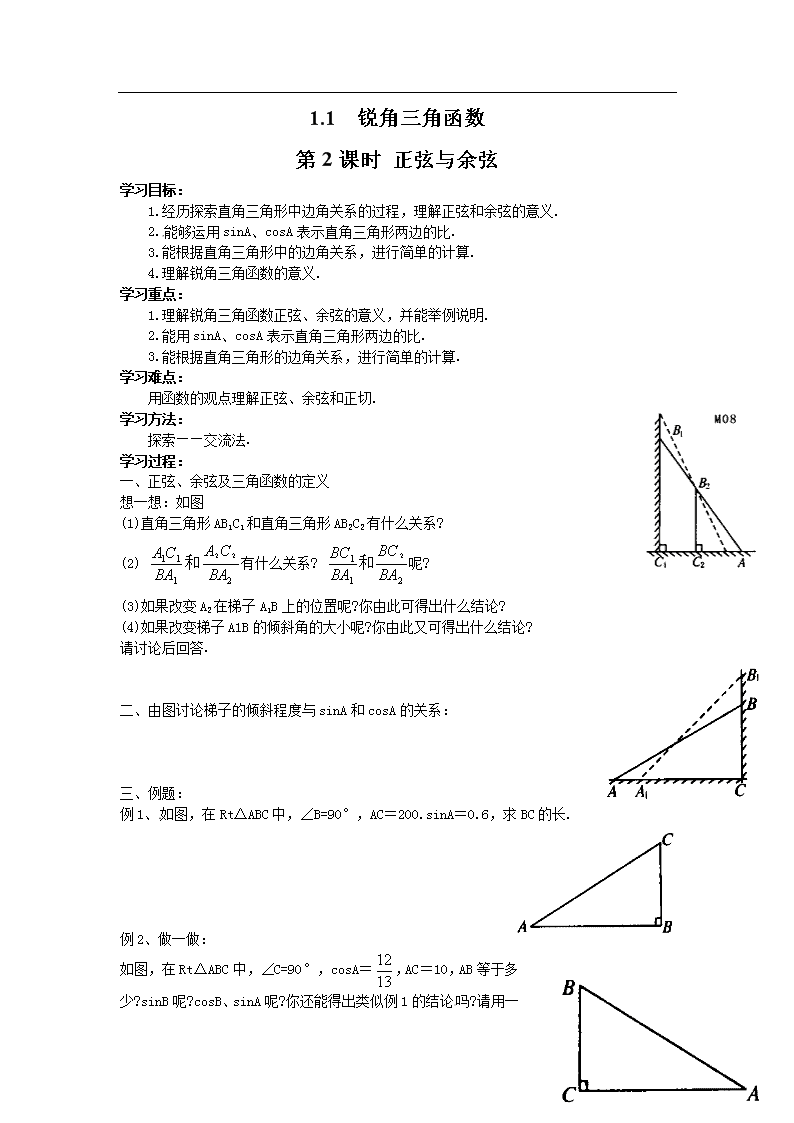
1.1 锐角三角函数 第2课时 正弦与余弦 学习目标: 1.经历探索直角三角形中边角关系的过程,理解正弦和余弦的意义. 2.能够运用sinA、cosA表示直角三角形两边的比. 3.能根据直角三角形中的边角关系,进行简单的计算. 4.理解锐角三角函数的意义. 学习重点: 1.理解锐角三角函数正弦、余弦的意义,并能举例说明. 2.能用sinA、cosA表示直角三角形两边的比. 3.能根据直角三角形的边角关系,进行简单的计算. 学习难点: 用函数的观点理解正弦、余弦和正切. 学习方法: 探索——交流法. 学习过程: 一、正弦、余弦及三角函数的定义 想一想:如图 (1)直角三角形AB1C1和直角三角形AB2C2有什么关系? (2) 有什么关系? 呢? (3)如果改变A2在梯子A1B上的位置呢?你由此可得出什么结论? (4)如果改变梯子A1B的倾斜角的大小呢?你由此又可得出什么结论? 请讨论后回答. 二、由图讨论梯子的倾斜程度与sinA和cosA的关系: 三、例题: 例1、如图,在Rt△ABC中,∠B=90°,AC=200.sinA=0.6,求BC的长. 例2、做一做: 如图,在Rt△ABC中,∠C=90°,cosA=,AC=10,AB等于多少?sinB呢?cosB、sinA呢?你还能得出类似例1的结论 吗?请用一般式表达. 四、随堂练习: 1、在等腰三角形ABC中,AB=AC=5,BC=6,求sinB,cosB,tanB. 2、在△ABC中,∠C=90°,sinA=,BC=20,求△ABC的周长和面积. [来源:Zxxk.Com] 3、在△ABC中.∠C=90°,若tanA=,则sinA= . 4、已知:如图,CD是Rt△ABC的斜边AB上的高,求证:BC2=AB·BD.(用正弦、余弦函数的定义证明)[来源:学科网] 五、课后练习: 1、在Rt△ABC中,∠ C=90°,tanA=,则sinB=_______,tanB=______. 2、在Rt△ABC中,∠C=90°,AB=41,sinA=,则AC=______,BC=_______. 3、在△ABC中,AB=AC=10,sinC=,则BC=_____.[来源:学科网ZXXK] 4、在△ABC中,已知AC=3,BC=4,AB=5,那么下列结论正确的是( ) A.sinA= B.cosA= C.tanA= D.cosB= 5、如图,在△ABC中,∠C=90°,sinA=,则等于( ) A. B. C. D. 6、Rt△ABC中,∠C=90°,已知cosA=,那么tanA等于( ) A. B. C. D. 7、在△ABC中,∠C=90°,BC=5,AB=13,则sinA的值是 A. B. C. D. 8、已知甲、乙两坡的坡角分别为α、β, 若甲坡比乙坡更徒些, 则下列结论正确的是( ) A.tanα查看更多