2017-2018学年黑龙江省大庆铁人中学高二上学期期末考试数学（文）试题（Word版）

2017-2018学年黑龙江省大庆铁人中学高二上学期期末考试数学（文）试题（Word版）

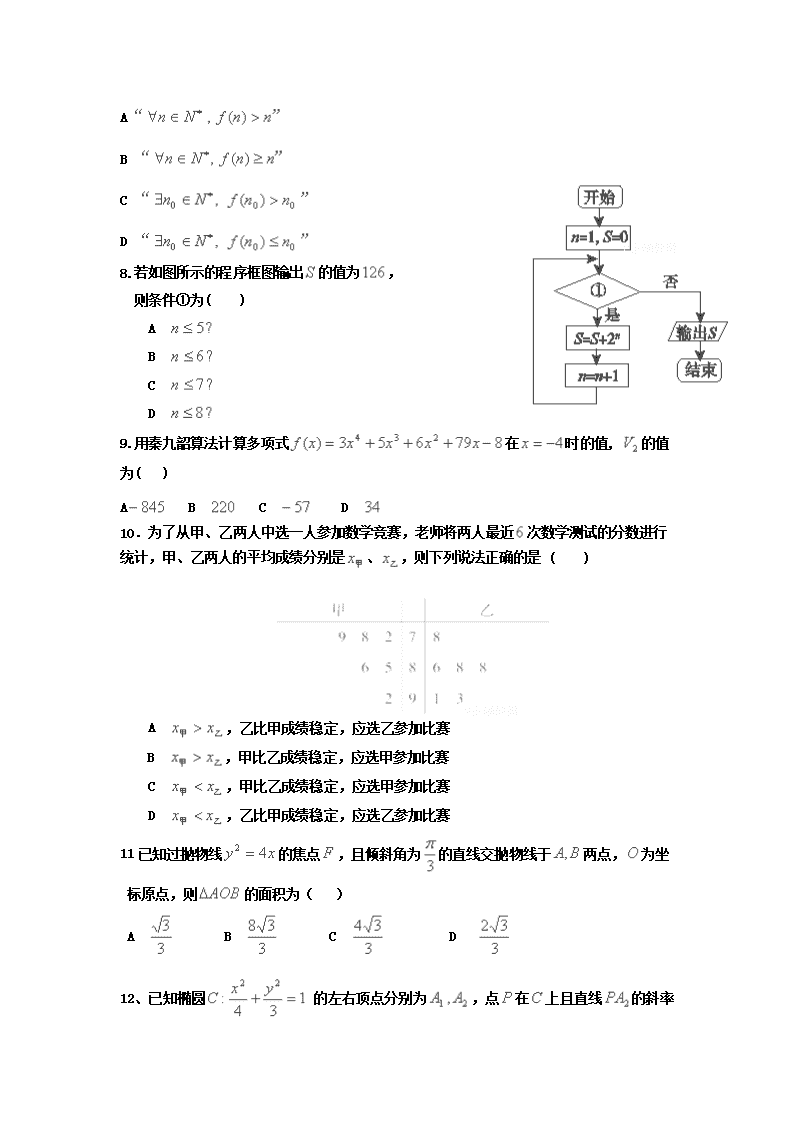
‎2017-2018学年黑龙江省大庆铁人中学高二上学期期末考试数学试题（文） ‎ 试题说明：1、本试题满分 150 分，答题时间 120 分钟。 ‎ ‎2、请将答案填写在答题卡上，考试结束后只交答题卡。‎ 第Ⅰ卷 选择题部分 一、选择题（每小题只有一个选项正确，每小题5分，共60分。）‎ ‎1.用“辗转相除法”求得和的最大公约数是( ) 　　　‎ A B C D ‎ ‎2.已知命题 ;命题若，则,下列命题为真命题的是(　　)‎ A B C D ‎3．某校选修乒乓球课程的学生中，高一年级有名，高二年级有名．现用分层抽样的方法在这名学生中抽取一个样本，已知在高一年级的学生中抽取了名，则在高二年级的学生中应抽取的人数为(　　) ‎ A B C D ‎ ‎4将直线变换为直线的一个伸缩变换为(　　)‎ A B C D ‎5．是“方程”表示双曲线的(　　)‎ A充要条件　　B充分不必要条件 C必要不充分条件 D既不充分也不必要条件 ‎6. 甲、乙、丙、丁四位同学各自对两变量的线性相关性做试验，并用回归分析方法分别求得相关系数与残差平方和如下表：‎ 甲 乙 丙 丁 ‎0.82‎ ‎0.78‎ ‎0.69‎ ‎0.85‎ ‎106‎ ‎115‎ ‎124‎ ‎103‎ 则哪位同学的试验结果体现线性相关性更强(　　)‎ A 甲 B 乙 C 丙 D 丁 ‎7.命题的否定形式是　(　　)‎ A ‎ B ‎ C ‎ D ‎ ‎8.若如图所示的程序框图输出的值为，‎ 则条件①为(　　)‎ A ‎ B ‎ C ‎ D ‎ ‎9.用秦九韶算法计算多项式在时的值, 的值为( ) ‎ A B C D ‎ ‎10．为了从甲、乙两人中选一人参加数学竞赛，老师将两人最近次数学测试的分数进行统计，甲、乙两人的平均成绩分别是、，则下列说法正确的是 (　　) ‎ A ，乙比甲成绩稳定，应选乙参加比赛 B ，甲比乙成绩稳定，应选甲参加比赛 C ，甲比乙成绩稳定，应选甲参加比赛 D ，乙比甲成绩稳定，应选乙参加比赛 ‎11已知过抛物线的焦点，且倾斜角为的直线交抛物线于两点，为坐标原点，则的面积为（ ）‎ A B C D ‎ ‎12、已知椭圆的左右顶点分别为，点在上且直线 的斜率的取值范围是，那么直线的斜率的取值范围是（ ）　‎ A B C D ‎ 第Ⅱ卷 解答题部分 二、填空题（本大题共有4个小题，每小题5分，共20分）‎ ‎13. 把化为二进制数为______________；‎ ‎14.在随机数模拟试验中，若,,,,‎ 表示生成之间的均匀随机数,共产生了个点，其中有个点满足，则椭圆的面积可估计为 ________ 。‎ ‎15.采用系统抽样方法从人中抽取人做问卷调查，为此将他们随机编号为,分组后在第一组采用简单随机抽样的方法抽到的号码为，抽到的人中，编号落入区间的人做问卷,编号落入区间的人做问卷B，其余的人做问卷C，则抽到的人中，做问卷B的人数为__________；‎ ‎16.在平面直角坐标系中,以坐标原点为极点,轴的非负半轴为极轴建立极坐标系.已知曲线 ‎：,直线:(为参数).曲线与直线相交于两点,则______ 。‎ 三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）‎ ‎17. (本小题满分10分) ‎ ‎ 某中学调查了某班全部45名同学参加书法社团和演讲社团的情况，数据如下：（单位：人）‎ 参加书法社团 未参加书法社团 参加演讲社团 未参加演讲社团 ‎（1）从该班随机选1名同学，求该同学至少参加上述一个社团的概率；‎ ‎（2）在既参加书法社团又参加演讲社团的名同学中，有名男同学和名女同学，现从这名男同学和名女同学中各随机选1人，求被选中且未被选中的概率。‎ ‎18.(12分)已知在平面直角坐标系中,曲线的参数方程为(θ为参数),‎ 直线经过定点,倾斜角为.‎ ‎(1)写出直线的参数方程和曲线C的标准方程.‎ ‎(2)设直线与曲线相交于两点,求的值.‎ ‎19．(本小题满分12分)‎ 以下是某地搜集到的新房屋的销售价格(单位：万元)和房屋的面积(单位：)的数据：‎ 房屋面积 ‎115‎ ‎110‎ ‎80‎ ‎135‎ ‎105‎ 销售价格 ‎24. 8‎ ‎21. 6‎ ‎18. 4‎ ‎29. 2‎ ‎22‎ ‎(1) 求线性回归方程;（提示：见第（2）问下方参考数据）‎ ‎(2)并据(1)的结果估计当房屋面积为150 m2时的销售价格(精确到0. 1万元)．‎ ＝i＝109， ＝23. 2， (xi－)2＝1570， (xi－)(yi－)＝308‎ ‎ ， ‎ ‎20.(本小题满分12分)‎ 已知过抛物线的焦点，斜率为的直线交抛物线于、两点，且 ‎ ‎(1)求该抛物线的方程；‎ ‎(2) 为坐标原点，为抛物线上一点，若，求的值．‎ ‎21.(本小题满分12分)‎ 某校从参加高一年级期末考试的学生中抽出名学生，将其成绩（均为整数）分成六段，‎ ‎，后画出如下部分频率分布直方图．观察图形的信息，回答下列问题：‎ ‎（1）求第四小组的频率，并补全这个频率分布直方图；‎ ‎（2）估计这次考试的及格率（分及以上为及格），众数和中位数；(保留整数)‎ ‎22．（本题满分12分）‎ 已知、分别是椭圆的左、右焦点。‎ ‎（I）若是第一象限内该椭圆上的一点，，求点的坐标；‎ ‎（II）设过定点的直线与椭圆交于不同的两点、，且为锐角（其中 为坐标原点），求直线的斜率的取值范围。‎ ‎ ‎ ‎ 数学试题答案（文）‎ 一、选择题（每小题只有一个选项正确，每小题5分，共60分。）‎ ‎1-6 DBBABD 7—12 CBDDCD ‎ 二、填空题（本大题共有4个小题，每小题5分，共20分）‎ ‎13． 14. 15. 11 16. ‎ 三、解答题 ‎17. (本小题满分10分) ‎ 解析：（1）设事件A：至少参加上述一个社团 未参加书法比赛又没参加演讲社团的有30人，所以至少参加上述一个社团的共有45-30=15（人）‎ 所以 ‎（2）‎ ‎18.(12分)已知在平面直角坐标系中,曲线的参数方程为(θ为参数),‎ 直线经过定点,倾斜角为.‎ ‎(1)写出直线的参数方程和曲线C的标准方程.‎ ‎(2)设直线与曲线相交于两点,求的值.‎ ‎【解题】(1)根据直线经过的点和倾斜角求直线的参数方程,消去参数得圆的普通方程.‎ ‎(2)将直线的参数方程代入圆的普通方程,利用参数的几何意义求值.‎ ‎【解析】(1)圆C:(x-1)2+(y-2)2=16, ………………………………….3‎ 直线: (t为参数). …………………………………6‎ ‎(2)将直线的参数方程代入圆的方程得:, ‎ 设t1,t2是方程的两个根,则t1t2=-3,‎ 所以|PA||PB|=|t1||t2|=|t1t2|=3. ………………………………….12‎ ‎19．(本小题满分12分)‎ 以下是某地搜集到的新房屋的销售价格(单位：万元)和房屋的面积(单位：)的数据：‎ 房屋面积 ‎115‎ ‎110‎ ‎80‎ ‎135‎ ‎105‎ 销售价格 ‎24. 8‎ ‎21. 6‎ ‎18. 4‎ ‎29. 2‎ ‎22‎ ‎(1) 求线性回归方程;‎ ‎(2)并据(1)的结果估计当房屋面积为‎150 m2‎时的销售价格(精确到0. 1万元)．‎ ‎ ， ‎ 解析]　 (1)＝i＝109， ＝23. 2，…………………………………2‎ (xi－)2＝1570，(xi－)(yi－)＝308．………………………………….4‎ 则＝＝≈0. 1962，……6‎ ＝－＝23. 2－0. 1962×109＝1. 8142．‎ 故所求回时直线方程为＝0. 1962x＋1. 8142. …………………………………8‎ ‎(2)由(1)得： 当x＝150时，销售价格的估计值为＝0. 196×150＋1. 8142＝31. 2442≈31. 2(万元)．‎ 答: 当房屋面积为‎150 m2‎时的销售价格估计为31. 2(万元)．…………………………………12‎ ‎20．文(本小题满分12分)已知过抛物线y2＝2px(p>0)的焦点，斜率为2的直线交抛物线于A(x1，y1)，B(x2，y2)(x1

查看更多