黑龙江省伊春市第二中学2020届高三上学期期末考试数学（文）试题 含答案

黑龙江省伊春市第二中学2020届高三上学期期末考试数学（文）试题 含答案

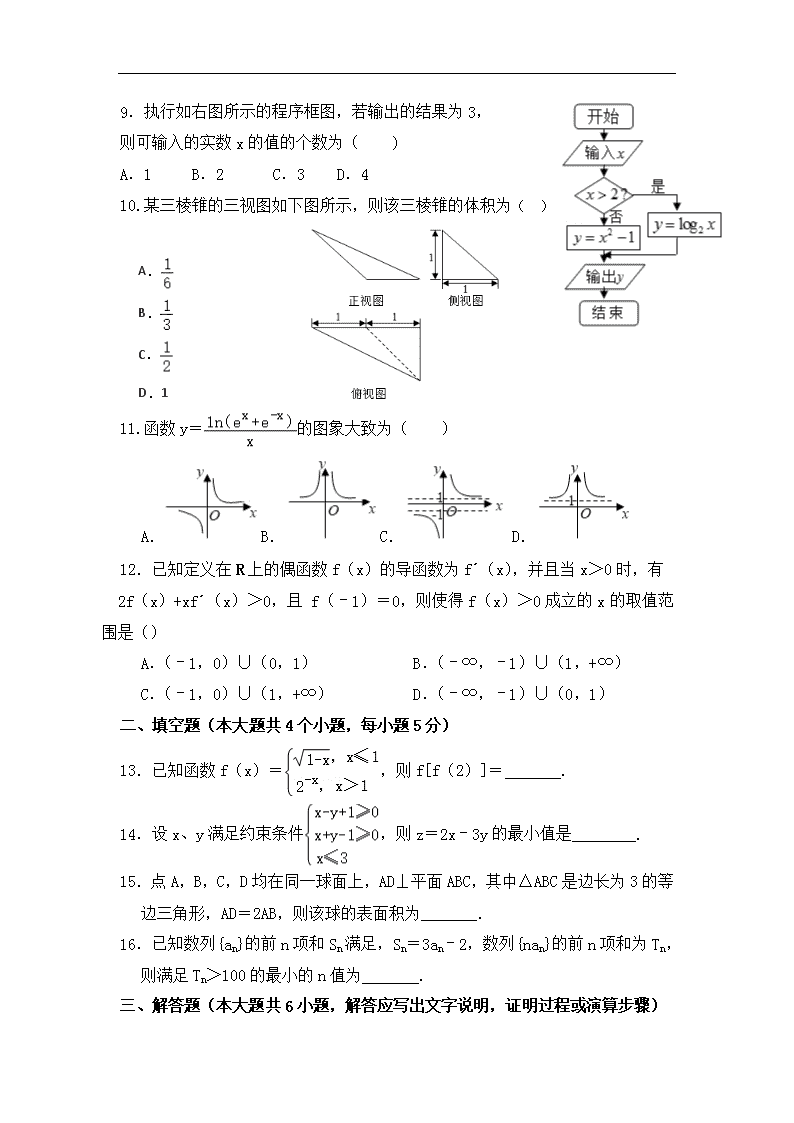
伊春市第二中学2019-2020学年度第一学期期末考试 高三学年 文科数学试卷 分值：150分 时间：120分钟 一、选择题（每小题5分，每题只有一个正确选项）‎ ‎1．已知集合A＝{x|（x+1）（x﹣3）＜0}，B＝{1，2，3}，则A∩B＝（　　）‎ A．{x|﹣1＜x＜3} B．{x|1≤x≤2} C．{1，2，3} D．{1，2}‎ ‎2．已知复数z满足（1+i）z＝2i，则z＝（　　）‎ A．1﹣i B．1+i C．﹣1﹣i D．﹣1+i ‎3．命题“∃α∈R，sinα＝‎0”‎的否定是（　　）‎ A．∃α∈R，sinα≠0 B．∀α∈R，sinα≠0 ‎ C．∀α∈R，sinα＜0 D．∀α∈R，sinα＞0‎ ‎4．下列函数中，既是奇函数又在（﹣∞，+∞）上单调递增的是（　　）‎ A．y＝sinx B．y＝ ‎ C．y＝﹣ D．y＝‎ ‎5．已知向量＝（2，﹣1），＝（0，1），（+k）•＝3，则k＝（　　）‎ A．﹣2 B．‎2 ‎C．﹣4 D．4‎ ‎6．在等差数列{an}中，是方程x2+6x+2＝0的两个实根，则＝（　　）‎ A． B．﹣‎3 ‎C．﹣6 D．2‎ ‎7．将包含甲、乙两人的4位同学平均分成2个小组参加某项公益活动，则甲、乙两名同学分在同一小组的概率为（　　）‎ A． B． C． D．‎ ‎8.已知双曲线（a＞0）的一条渐近线为y＝，则双曲线的焦点坐标为（　　）‎ A．（±，0） B．（±，0） C．（0，±） D．（0，±）‎ ‎9．执行如右图所示的程序框图，若输出的结果为3，‎ 则可输入的实数x的值的个数为（　　)‎ A．1 B．‎2 ‎C．3 D．4‎ ‎10.某三棱锥的三视图如下图所示，则该三棱锥的体积为（　）‎ A． ‎ ‎ B． ‎ ‎ C． ‎ ‎ D． ‎1‎ ‎11.函数y＝的图象大致为（　　）‎ A．B．C． D．‎ 12． 已知定义在R上的偶函数f（x）的导函数为f´（x），并且当x＞0时，有 ‎2f‎（x）+xf´（x）＞0，且 f（﹣1）＝0，则使得f（x）＞0成立的x的取值范围是（）‎ A．（﹣1，0）∪（0，1） B．（﹣∞，﹣1）∪（1，+∞） ‎ C．（﹣1，0）∪（1，+∞） D．（﹣∞，﹣1）∪（0，1）‎ 二、填空题（本大题共4个小题，每小题5分）‎ ‎13．已知函数f（x）＝，则f[f（2）]＝　 　．‎ ‎14．设x、y满足约束条件，则z＝2x﹣3y的最小值是________.‎ ‎15．点A，B，C，D均在同一球面上，AD⊥平面ABC，其中△ABC是边长为3的等边三角形，AD＝2AB，则该球的表面积为　 　．‎ ‎16．已知数列{an}的前n项和Sn满足，Sn＝3an﹣2，数列{nan}的前n项和为Tn，则满足Tn＞100的最小的n值为　 　．‎ 三、解答题（本大题共6小题，解答应写出文字说明，证明过程或演算步骤）‎ ‎17．在△ABC中，∠A，∠B，∠C的对边分别为a，b，c，若bcos C＝(‎2a－c)cos B，‎ ‎(Ⅰ)求∠B的大小；(Ⅱ)若b＝，a＋c＝4，求a,c的值.‎ ‎18．在某次测验中，某班40名考生的成绩满分100分统计如下图所示．‎ ‎（Ⅰ）估计这40名学生的测验成绩的中位数x0精确到0.1；‎ ‎（Ⅱ）记80分以上为优秀，80分及以下为合格，结合频率分布直方图完成下表，并判断是否有95%的把握认为数学测验成绩与性别有关？‎ 合格 优秀 合计 男生 ‎16‎ 女生 ‎4‎ 合计 ‎40‎ P（x2≥k0） ‎ ‎0.050‎ ‎0010‎ ‎0.001‎ k0‎ ‎3.841‎ ‎6.635‎ ‎10.828‎ 附：‎ x2＝‎ ‎19．如图所示，在四棱锥P﹣ABCD中，PA⊥平面ABCD，AD∥BC，AB⊥BC，AP＝AD＝2AB＝2BC＝2，点M在棱PC上． ‎ ‎（Ⅰ）求证：AM⊥CD；‎ ‎（Ⅱ）当AM⊥平面PCD时，求三棱锥M﹣PAD的体积．‎ ‎20．已知椭圆C：+＝1（a＜b＜0）的离心率为，短轴长为4．‎ ‎（Ⅰ）求椭圆C的方程；‎ ‎（Ⅱ）过点N（0，2）作两条直线，分别交椭圆C于A， B两点（异于N），当直线NA，NB的斜率之和为4时，直线AB恒过定点，求出定点的坐标．‎ ‎21．已知函数f（x）＝．‎ ‎（1）若f（x）在（0，+∞）上单调递增，求a的取值范围；‎ ‎（2）当a＝1且x＞0时，f（x）＞mln（x+1），求m的取值范围．‎ ‎22.已知在直角坐标系xOy中，圆锥曲线C的参数方程为（θ为参数），直线经过定点P（2，3），倾斜角为．‎ ‎（1）写出直线的参数方程和圆的标准方程；‎ ‎（2）设直线与圆相交于A，B两点，求｜PA｜·｜PB｜的值． ‎ 高三文科数学参考答案与试题解析 一．选择题（共14小题）‎ ‎1．已知集合A＝{x|（x+1）（x﹣3）＜0}，B＝{1，2，3}，则A∩B＝（　　）‎ A．{x|﹣1＜x＜3} B．{x|1≤x≤2} C．{1，2，3} D．{1，2}‎ ‎【解答】解：A＝{x|﹣1＜x＜3}；‎ ‎∴A∩B＝{1，2}．‎ 故选：D．‎ ‎2．已知复数z满足（1+i）z＝2i，则z＝（　　）‎ A．1﹣i B．1+i C．﹣1﹣i D．﹣1+i ‎【解答】解：∵复数z满足（1+i）z＝2i，∴（1﹣i）（1+i）z＝（1﹣i）×2i，化为2z＝2（i+1），∴z＝1+i．‎ 故选：B．‎ ‎3．命题“∃α∈R，sinα＝‎0”‎的否定是（　　）‎ A．∃α∈R，sinα≠0 B．∀α∈R，sinα≠0 ‎ C．∀α∈R，sinα＜0 D．∀α∈R，sinα＞0‎ ‎【解答】解：特称命题的否定是全称命题，‎ ‎∴∃α∈R，sinα＝0的否定为：∀α∈R，sinα≠0，‎ 故选：B．‎ ‎4．下列函数中，既是奇函数又在（﹣∞，+∞）上单调递增的是（　　）‎ A．y＝sinx B．y＝|x| ‎ C．y＝﹣x3 D．y＝ln（+x）‎ ‎【解答】解：根据题意，依次分析选项：‎ 对于A，y＝sinx，为正弦函数，在（﹣∞，+∞）上不是单调函数，不符合题意；‎ 对于B，y＝|x|，为偶函数，不符合题意；‎ 对于C，y＝﹣x3，是奇函数但在（﹣∞，+∞）上单调递减，不符合题意；‎ 对于D，y＝lnx（+x），既是奇函数又在（﹣∞，+∞）上单调递增，符合题意；‎ 故选：D．‎ ‎5．已知向量＝（2，﹣1），＝（0，1），（+k）•＝3，则k＝（　　）‎ A．﹣2 B．‎2 ‎C．﹣4 D．4‎ ‎【解答】解：因为＝（2，﹣1），＝（0，1），‎ 所以（+k）•＝+k2＝﹣1+k＝3，‎ 解得k＝4，‎ 故选：D．‎ ‎6．在等差数列{an}中，a2，a14是方程x2+6x+2＝0的两个实根，则＝（　　）‎ A． B．﹣‎3 ‎C．﹣6 D．2‎ ‎【解答】解：∵a2，a14是方程x2+6x+2＝0的两个实根，‎ ‎∴a2+a14＝﹣6，a‎2a14＝2，‎ 由等差数列的性质可知，a2+a4＝‎2a8＝﹣6，‎ ‎∴a8＝﹣3‎ 则＝，‎ 故选：A．‎ ‎7．将包含甲、乙两人的4位同学平均分成2个小组参加某项公益活动，则甲、乙两名同学分在同一小组的概率为（　　）‎ A． B． C． D．‎ ‎【解答】解：将包含甲、乙两人的4位同学平均分成2个小组，共有＝3种方法，甲、乙两名同学分在同一小组，共有1种方法 所以甲、乙两名同学分在同一小组的概率为 故选：C．‎ ‎8．已知双曲线（a＞0）的一条渐近线方程为y＝，则双曲线的焦点坐标为（　　）‎ A．（±，0） B．（±，0） C．（0，±） D．（0，±）‎ ‎【解答】解：双曲线（a＞0）的渐近线方程为y＝±x，‎ 由题意可得＝，即有a＝2，‎ 则双曲线的b＝，c＝＝，‎ 即有双曲线的焦点为（0，±），‎ 故选：D．‎ ‎9．执行如图所示的程序框图，若输出的结果为3，则可输入的实数x的值的个数为（　　）‎ A．1 B．‎2 ‎C．3 D．4‎ ‎【解答】解：根据题意，该框图的含义是 当x≤2时，得到函数y＝x2﹣1；当x＞2时，得到函数y＝log2x．‎ 因此，若输出结果为3时，‎ ‎①若x≤2，得x2﹣1＝3，解之得x＝±2‎ ‎②当x＞2时，得y＝log2x＝3，得x＝8‎ 因此，可输入的实数x值可能是2，﹣2或8，共3个数．‎ 故选：C．‎ ‎10．某三棱锥的三视图如图所示，则该三棱锥的体积为（　　）‎ A． B． C． D．1‎ ‎【解答】解：由已知中的三视图可得：该几何体是一个以俯视图为底面的三棱锥，‎ 棱锥的底面面积S＝×1×1＝，‎ 高为1，‎ 故棱锥的体积V＝＝，‎ 故选：A．‎ ‎11．函数y＝的图象大致为（　　）‎ A． B． ‎ C． D．‎ ‎【解答】解：根据题意，y＝，其定义域为{x|x≠0}，‎ 有f（﹣x）＝﹣＝﹣f（x），即函数f（x）为奇函数，排除B、D；‎ 当x＞0时，e﹣x＞0，则有ln（ex+e﹣x）＞ln（ex）＝x，必有＞1，排除A；‎ 故选：C．‎ ‎12．已知定义在R上的偶函数f（x）的导函数为f'（x），当x＞0时，有‎2f（x）+xf'（x）＞0，且f（﹣1）＝0，则使得f（x）＞0成立的x的取值范围是（　　）‎ A．（﹣1，0）∪（0，1） B．（﹣∞，﹣1）∪（1，+∞） ‎ C．（﹣1，0）∪（1，+∞） D．（﹣∞，﹣1）∪（0，1）‎ ‎【解答】解：当x＞0时，由‎2f（x）+xf'（x）＞0可知：两边同乘以x得：‎ ‎2xf（x）+x‎2f′（x）＞0，设：g（x）＝x‎2f（x），‎ 则g′（x）＝2xf（x）+x‎2f′（x）＞0，恒成立：‎ ‎∴g（x）在（0，+∞）单调递增，定义在R上的偶函数f（x），f（﹣1）＝0，可得f（1）＝0，‎ 函数f（x）的图象如图：‎ 当x＞0；f（x）＞0成立的x的取值范围是：x＞1，‎ 当x＜0时，函数是偶函数，同理得：x＜﹣1，‎ 综上可知：实数x的取值范围为（﹣∞，﹣1）∪（1，+∞），‎ 故选：B．‎ ‎13．已知函数f（x）＝，则f[f（2）]＝　　．‎ ‎【解答】解：∵函数f（x）＝，‎ ‎∴f（2）＝2﹣2＝，‎ f[f（2）]＝f（）＝＝．‎ 故答案为：．‎ ‎14．设x、y满足约束条件，则z＝2x﹣3y的最小值是 ‎【解答】解：由z＝2x﹣3y得y＝，‎ 作出不等式组对应的平面区域如图（阴影部分ABC）：‎ 平移直线y＝，由图象可知当直线y＝，过点A时，直线y＝截距最大，此时z最小，‎ 由得，即A（3，4），‎ 代入目标函数z＝2x﹣3y，‎ 得z＝2×3﹣3×4＝6﹣12＝﹣6．‎ ‎∴目标函数z＝2x﹣3y的最小值是﹣6．‎ ‎15．点A，B，C，D均在同一球面上，AD⊥平面ABC，其中△ABC是等边三角形，AD＝2AB＝6，则该球的表面积为　48π　．‎ ‎【解答】解：如图，O′为底面的中心，OO′⊥底面ABC，‎ E为AD中点，且OE⊥AD，‎ 在正三角形ABC中，由AB＝3求得，‎ 又OO′＝AE＝3，‎ ‎∴OA＝2，‎ ‎∴S球＝4π×12＝48π，‎ 故答案为：48π．‎ ‎16．已知数列{an}的前n项和Sn满足，Sn＝3an﹣2，数列{nan}的前n项和为Tn，则满足Tn＞100的最小的n值为　7　．‎ ‎【解答】解：根据题意，数列{an}满足Sn＝3an﹣2，①‎ 当n≥2时，有Sn﹣1＝3an﹣1﹣2，②，‎ ‎①﹣②可得：an＝3an﹣3an﹣1，变形可得2an＝3an﹣1，‎ 当n＝1时，有S1＝a1＝‎3a1﹣2，解可得a1＝1，‎ 则数列{an}是以a1＝1为首项，公比为的等比数列，则an＝（）n﹣1，‎ 数列{nan}的前n项和为Tn，则Tn＝1+2×+3×（）2+……+n×（）n﹣1，③‎ 则有Tn＝+2×（）2+3×（）3+……+n×（）n，④‎ ‎③﹣④可得：﹣Tn＝1+（）+（）2+……×（）n﹣1﹣n×（）n＝﹣2（1﹣）﹣n×（）n，‎ 变形可得：Tn＝4+（2n﹣4）×（）n，‎ 若Tn＞100，即4+（2n﹣4）×（）n＞100，‎ 分析可得：n≥7，故满足Tn＞100的最小的n值为7；‎ 故答案为：7．‎ ‎17. （1）sinBcos C＝(2sinA－sinc)cos B ‎ sin(B+C)=2sinAcosB ‎ cosB=，B=。‎ ‎（2）a=3,c=1或a=1,c=3。‎ ‎18．在某次测验中，某班40名考生的成绩满分100分统计如图所示．‎ ‎（Ⅰ）估计这40名学生的测验成绩的中位数x0精确到0.1；‎ ‎（Ⅱ）记80分以上为优秀，80分及以下为合格，结合频率分布直方图完成下表，并判断是否有95%的把握认为数学测验成绩与性别有关？‎ 合格 优秀 合计 男生 ‎16‎ 女生 ‎4‎ 合计 ‎40‎ 附：‎ P（x2≥k0） ‎ ‎0.050‎ ‎0010‎ ‎0.001‎ k0‎ ‎3.841‎ ‎6.635‎ ‎10.828‎ x2＝‎ ‎【解答】解：（Ⅰ）由频率分布直方图易知：‎ ‎0.01×10+0.015×10+0.02×10＝0.45；‎ 即分数在[40，70）的频率为：0.45，‎ 所以0.03×（x0﹣70）＝0.5﹣0.45，‎ 解得：x0＝≈71.7；‎ ‎∴40名学生的测验成绩的中位数为71.7；‎ ‎（Ⅱ）由频率分布直方图，可得列联表如下：‎ 合格 优秀 合计 男生 ‎16 ‎ ‎6 ‎ ‎22 ‎ 女生 ‎14‎ ‎ 4‎ ‎ 18‎ 合计 ‎ 30‎ ‎ 10‎ ‎ 40‎ X2＝＝≈0.135＜3.841；‎ 所以没有95%的把握认为数学测验成绩与性别有关．‎ ‎19．如图所示，在四棱锥P﹣ABCD中，PA⊥平面ABCD，AD∥BC，AB⊥BC，AP＝AD＝2AB＝2BC＝2，点M在棱PC上．‎ ‎（Ⅰ）求证：AM⊥CD；‎ ‎（Ⅱ）当AM⊥平面PCD时，求三棱锥M﹣PAD的体积．‎ ‎【解答】证明：（Ⅰ）设AD中点为E，连接AC、CE，由题意AE＝BC，‎ ‎∵AD∥BC，∴四边形ABCE为平行四边形．‎ 又AB⊥BC，AB＝BC＝1，∴ABCE为正方形．‎ 在Rt△CDE中，CD＝，又AC＝，AD＝2，‎ ‎∴AC2+CD2＝AD2，∴CD⊥AC．‎ ‎∵PA⊥平面ABCD，CD⊂平面ABCD，∴PA⊥CD．‎ ‎∵PA，AC⊂平面PAC，且PA∩AC＝A，‎ ‎∴CD⊥平面PAC．‎ ‎∵AM⊂平面PAC，∴AM⊥CD．‎ 解（Ⅱ）由已知AM⊥平面PCD，∴AM⊥PC．‎ ‎∵AC＝，PC＝，，‎ ‎∴AM＝，PM＝，∴PM＝，‎ C到平面PAD的距离等于B到平面PAD的距离，‎ 所以三棱锥M﹣PAD的高h＝＝，‎ ‎∴三棱锥M﹣PAD的体积VM﹣PAD＝＝．‎ ‎20．已知椭圆C：+＝1（a＜b＜0）的离心率为，短轴长为4．‎ ‎（Ⅰ）求椭圆C的方程；‎ ‎（Ⅱ）过点N（0，2）作两条直线，分别交椭圆C于A，B两点（异于N），当直线NA，NB的斜率之和为4时，直线AB恒过定点，求出定点的坐标．‎ ‎【解答】解：（Ⅰ）由题意知：，2b＝4，a2﹣c2＝b2．‎ 解得a＝2，b＝c＝2，所以椭圆方程为．‎ ‎（Ⅱ）当直线AB的斜率存在时，设直线AB方程为y＝kx+m（k≠0），A（x1，y1），B（x2，y2）．‎ 由由kNA+kNB＝4，得，‎ 整理可得2kx1x2+（m﹣2）（x1+x2）＝4x1x2（*）‎ 联立，消去y得（1+2k2）x2+4kmx+‎2m2‎﹣8＝0，由题意知二次方程有两个不等实根，‎ ‎∴，．‎ 代入（*）得，整理得整理可得（m﹣2）（k﹣m﹣2）＝0，．‎ ‎∵∵m≠2，∴m＝k﹣2，∴y＝kx+k﹣2，y+2＝k（x+1），所以直线AB恒过定点（﹣1，﹣2）．‎ ‎ 当直线AB的斜率不存在时，设直线AB的方程为x＝x0，A（x0，y1），B（x0，y2），其中y2＝﹣y1，∴y1+y2＝0，‎ 由kNA+kNB＝t，得，∴∴x0＝﹣1．‎ ‎∴当直线AB的斜率不存在时，直线AB也过定点（﹣1，﹣2）．‎ 综上所述，直线AB恒过定点（﹣1，﹣2）．‎ ‎21．已知函数f（x）＝．‎ ‎（1）若f（x）在（0，+∞）上单调递增，求a的取值范围；‎ ‎（2）当a＝1且x＞0时，f（x）＞mln（x+1），求m的取值范围．‎ ‎【解答】解：（1）∵f（x）＝在（0，+∞）上单调递增，‎ ‎∴f′（x）＝，即xex﹣ex+a≥0．‎ 设g（x）＝xex﹣ex+a，则g′（x）＝xex＞0，‎ ‎∴g（x）＞g（0）＝a﹣1，则a﹣1≥0，得a≥1．‎ ‎（2）当a＝1时，f（x）＞mln（x+1）⇔ex﹣x﹣1＞mxln（x+1）⇔ex﹣x﹣1﹣mxln（x+1）＞0，‎ 设h（x）＝ex﹣x﹣1﹣mxln（x+1），则h′（x）＝，‎ 再令H（x）＝，则H′（x）＝．‎ 若m，∵x＞0，∴m（）＜1，则H′（x）＞0，h′（x）在（0，+∞）上单调递增，‎ h′（x）＞h′（0）＝0，∴h（x）是增函数，h（x）＞h（0）＝0，可得f（x）＞mln（x+1）成立；‎ 若m＞，H′（x）＝在（0，+∞）上单调递增，H′（0）＝1﹣‎2m＜0，‎ H′（ln（‎2m））＝‎2m﹣＝＞0．‎ ‎∴存在x0∈（0，ln（‎2m））使得H′（x0）＝0，当x∈（0，x0）时，H′（x）＜0，‎ ‎∴h（x）在（0，x0）上单调递减，可得h（x）＜h（0）＝0，即f（x）＞mln（x ‎+1）不成立．‎ 综上可得，m的取值范围为（﹣∞，]．‎ ‎22（t为参数），x2+y2=16‎ ‎(2)3‎