2020学年高二数学上学期期末联考试题 文（新版）人教版(1)

2020学年高二数学上学期期末联考试题 文（新版）人教版(1)

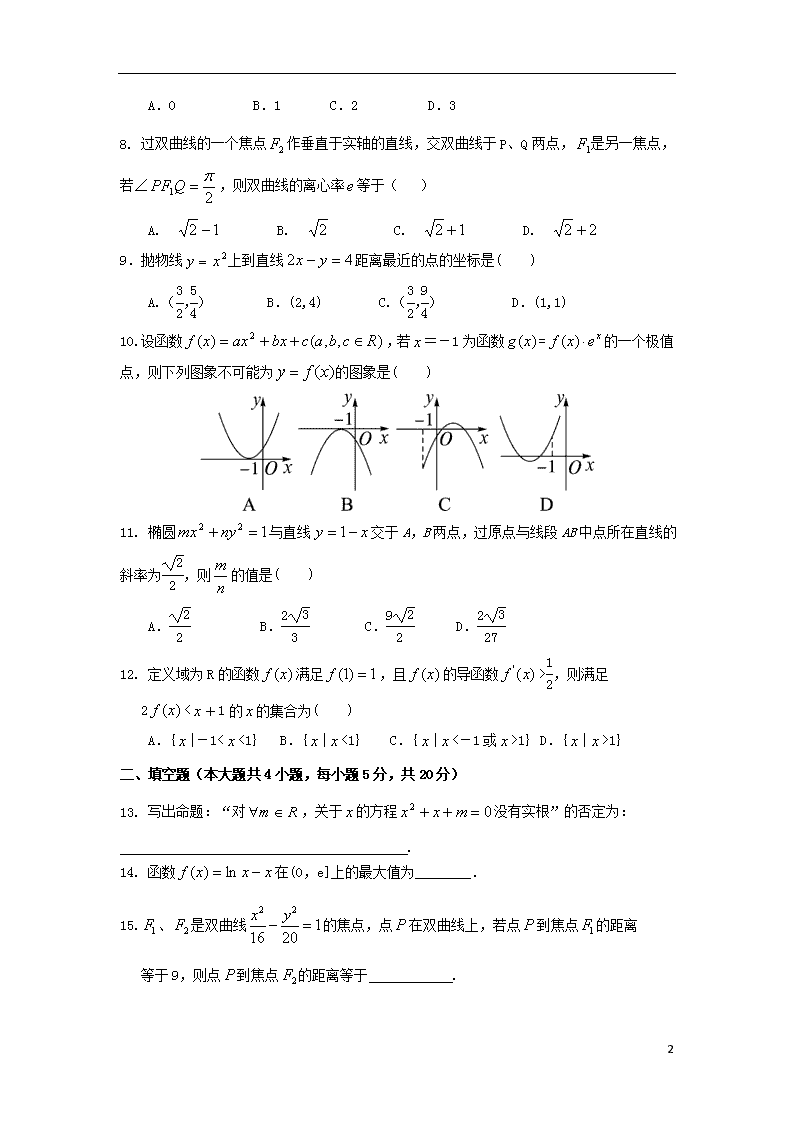
‎2019学年第一学期期末联考 高二文科数学试卷 ‎【完卷时间：120分钟 满分：150分】‎ 一、选择题（本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中,只有一项是符合题目要求的）‎ ‎1.已知是实数，则“且”是“且”的 ( )‎ ‎ A．充分而不必要条件 B．必要而不充分条件 ‎ ‎ C．充分必要条件 D．既不充分也不必要条件 ‎2．下列四个命题: ‎ ‎⑴“若则实数均为0”的逆命题；‎ ‎⑵ “相似三角形的面积相等”的否命题 ；‎ ‎⑶ “”逆否命题；‎ ‎⑷ “末位数不是0的数可被3整除”的逆否命题 ，其中真命题为( ) ‎ ‎ A． ⑴ ⑵ B．⑵ ⑶ C．⑴ ⑶ D．⑶ ⑷‎ ‎3.椭圆的焦点在轴上，长轴长是短轴长的两倍，则的值为( )‎ A. B. C．2 D．4‎ ‎4.抛物线的准线方程是（ ）‎ ‎ A．＝1 B．＝－1 C．＝－1 D．＝1‎ ‎5.已知双曲线:()的离心率为, 则的渐近线 ‎ 方程为（ ）‎ A． B． C． D．‎ ‎6.(　　)‎ A．－1 B．2 C．－2 D．‎ ‎7. 已知函数在[1，＋∞)内是单调增函数，则实数的最大值为( )‎ 9‎ A．0 B．1 C．2 D．3‎ ‎8. 过双曲线的一个焦点作垂直于实轴的直线，交双曲线于P、Q两点，是另一焦点，若∠，则双曲线的离心率等于（ ）‎ A. B. C. D. ‎ ‎9．抛物线上到直线距离最近的点的坐标是(　　)‎ A.（，） B．(2,4) C.（，） D．(1,1)‎ ‎10.设函数，若＝－1为函数=的一个极值点，则下列图象不可能为的图象是(　　)‎ ‎11. 椭圆与直线交于A，B两点，过原点与线段AB中点所在直线的斜率为，则的值是(　　)‎ A． B． C． D． ‎12. 定义域为R的函数满足，且的导函数>，则满足 ‎2<＋1的的集合为(　　)‎ A．{|－1<<1} B．{|<1} C．{|<－1或>1} D．{|>1}‎ 二、填空题（本大题共4小题，每小题5分，共20分）‎ ‎13. 写出命题：“对，关于的方程没有实根”的否定为：‎ ‎ .‎ ‎14. 函数在(0，e]上的最大值为________．‎ ‎15.、是双曲线的焦点，点在双曲线上，若点到焦点的距离 ‎ 等于9，则点到焦点的距离等于 .‎ ‎16.定义在上的可导函数，当时，恒成立，‎ 9‎ ‎，，，则的大小关系为 .‎ 三、解答题：(本大题6小题，共70分。解答应写出文字说明、证明过程或演算步骤)‎ ‎17.（本题满分10分）设 “关于的不等式的解集为”，‎ ‎：“方程表示双曲线” ．‎ ‎（1）若为真，求实数的取值范围；‎ ‎（2）若为假，为真，求实数的取值范围．‎ ‎18.（本题满分12分）已知函数在及处取得极值．‎ ‎(1)求、的值；‎ ‎(2)求的单调区间.‎ ‎19.（本题满分12分）已知与直线相切的动圆与圆 外切．‎ （1） 求圆心的轨迹C的方程；‎ （2） 若倾斜角为且经过点（2,0）的直线与曲线C相交于两点，‎ 求证：．‎ ‎20.（本小题满分12分））统计表明，某种型号的汽车在匀速行驶中每小时的耗油量（升）关于行驶速度（千米/小时）的函数解析式可以表示为：.已知甲、乙两地相距100千米.‎ ‎（1）当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地要耗油多少升？‎ ‎（2）当汽车以多大的速度匀速行驶时，从甲地到乙地耗油最少？最少为多少升？‎ 9‎ ‎21.（本小题满分12分）椭圆的离心率为，短轴长为2，若直线过点且与椭圆交于、两点．‎ （1） 求椭圆的标准方程；‎ ‎（2）求△面积的最大值.‎ ‎22.（本小题满分12分）设函数 ‎（1）若函数在（1，）处的切线过（0，1）点，求的值；‎ ‎（2）当时，试问，函数在[0，]是否存在极大值或极小值，说明理由．‎ 9‎ 福州市八县（市）协作校2016—2017学年第一学期期末联考 高二文科数学参考答案和评分标准 一、选择题（本大题共12小题，每小题5分，共60分）‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ C C A B C B D C D D A B 二、填空题（本大题共4小题，每小题5分，共20分）‎ ‎13．，关于x的方程x2＋x＋m＝0有实根. 14.－1‎ ‎15. 17 16. ‎ 三、解答题：(第17题10分，第18、19、20、21、22题都为12分，共70分。解答应写出文字说明、证明过程或演算步骤)‎ ‎17、解：（1）∵方程表示双曲线，‎ ‎∴若为真，则，．．．．．．．．．．．．．．．．．．．．．．．．．．．．2分 解得．．．．．．．．．．．．．．．．．．．．．．．．3分 ‎∴实数的取值范围为．．．．．．．．．．．．．．．．．．．．．．．．4分 ‎（2）若为真，则，．．．．．．．．．．．．．．．．．．．5分 即，解得．．．．．．．．．．．．．．．．．．．．．6分 ‎∵为假，为真，∴一真一假，．．．．．．．．．．．．．．．．．．．．．．．．．．7分 若真假，则；．．．．．．．．．．．．．．．．．．．．．．．．．．8分 若假真，则；．．．．．．．．．．．．．．．．．．．．．．．．．．9分 综上，的取值范围是．．．．．．．．．．．．．．．．．．．．10分 9‎ ‎18、解：（1）由已知．．．．．．．．．．．．．．．2分 因为在及处取得极值，所以1和2是方程的两根, 故、．．．．．．．．．．．．5分 ‎（2）由（1）可得 ‎ 当或时，，是单调递增的；．．．．．．．．．．．．8分 当时，，是单调递减的。．．．．．．．．．．．10分 所以，的单调增区间为和，的单调减区间为.．．．．．．．12分 ‎19、解：（1）法1：设动圆的半径为，‎ ‎∵ 圆与圆外切，∴，．．．．．．．．．．．．．．．．．1分 ‎∵圆与直线相切，∴圆心到直线的距离为，．．．．．．．．．．．．．2分 则圆心到直线的距离为，．．．．．．．．．．．．．．．．．．．．．．3分 ‎∴点到点与直线的距离相等，．．．．．．．．．．．．．．．．．．．．．．．．．．4分 即圆心的轨迹方程是抛物线．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．5分 法2：设动圆的半径为，点，则，‎ ‎∵圆与直线相切，∴，．．．．．．．．．．．．．．．．2分 ‎∵圆与圆外切，∴，．．．．．．．．．．．．．．．．．．．．3分 即，化简得．．．．．．．．．．．．．．．．．．．4分 即圆心的轨迹方程是抛物线．．．．．．．．．．．．．．．．．．．．．．．．．．．．．5分 9‎ ‎（2）直线的方程为，联立得，......7分 设，则．．．．．．．．．．．．．．．．．．．．．．．8分 ‎∵．．．．．．．．11分 ‎∴．．．．．．．．．．．．．．．．．．．．．．．．．．．12分 ‎20、解：（1）当时，汽车从甲地到乙地行驶了小时，．．．．．．．．．．．．．．．1分 ‎       耗油（升）‎ ‎    答：当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地耗油升.．．．．．．4分 ‎   （2）当速度为千米/小时时，汽车从甲地到乙地行驶了小时，设耗油量为升，‎ ‎       依题意得 ．．．．．．．．．．6分 ‎       则 ‎ ‎       令 得 ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．8分 ‎       当时，，是减函数；‎ ‎       当时，，是增函数.‎ ‎       故当时，取到极小值 ‎       因为在上只有一个极值，所以它是最小值.．．．．．．．．．11分 ‎       答：当汽车以80千米/‎ 9‎ 小时的速度匀速行驶时，从甲地到乙地耗油最少，最少为 升.．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．12分 ‎ 21、解：（1）由椭圆定义可知，，=2，求得．．．．．．．3分 故椭圆的标准方程为． ．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．4分 ‎（2）因为直线过点，可设直线的方程为 或（舍）．‎ 则整理得 ．．．．．．．．．．．．．．．．．6分 由．设． ‎ 解得 ， ．‎ 则 ． 因为 ‎ ． ．．．．．．．．．．．．．．．．．．．．9分 设，，．‎ 则在区间上为增函数．所以．‎ 所以，当且仅当时取等号，即．．．．．．．．．．．．11分 所以的最大值为．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．12分 9‎ ‎22、解：（1） f′（x）=ex+（x﹣1）ex﹣2kx=xex﹣2kx=x（ex﹣2k），．．．．．．．．．． 1分 f′（1）=e﹣2k，f（1）=﹣k，………………………………………………………2分 设切线方程为：y+k=（e﹣2k）（x﹣1），‎ 把（0，1）代入得k=e+1，…………………………………………………………4分 ‎（2）令f′（x）=0，得x1=0，x2=ln（2k），‎ 令g（k）=ln（2k）﹣k，k∈（，1]，……………………………………5分 则g′（k）=﹣1=≥0，‎ 所以g（k）在（，1]上单调递增，……………………………………………7分 所以g（k）≤g（1）=ln2﹣1=ln2﹣lne＜0，‎ 从而ln（2k）＜k，所以ln（2k）∈（0，k），…………………………………9分 所以当x∈（0，ln（2k））时，f′（x）＜0，f（x）单调递减；‎ 当x∈（ln（2k），+∞）时，f′（x）＞0，f（x）单调递增，………………11分 所以函数f（x）在[0，k]存在极小值，无极大值．…………………………12分 9‎