数学文卷·2018届黑龙江省大庆十中、二中、二十三中、二十八中高三第一次联合阶段检测（2017

数学文卷·2018届黑龙江省大庆十中、二中、二十三中、二十八中高三第一次联合阶段检测（2017

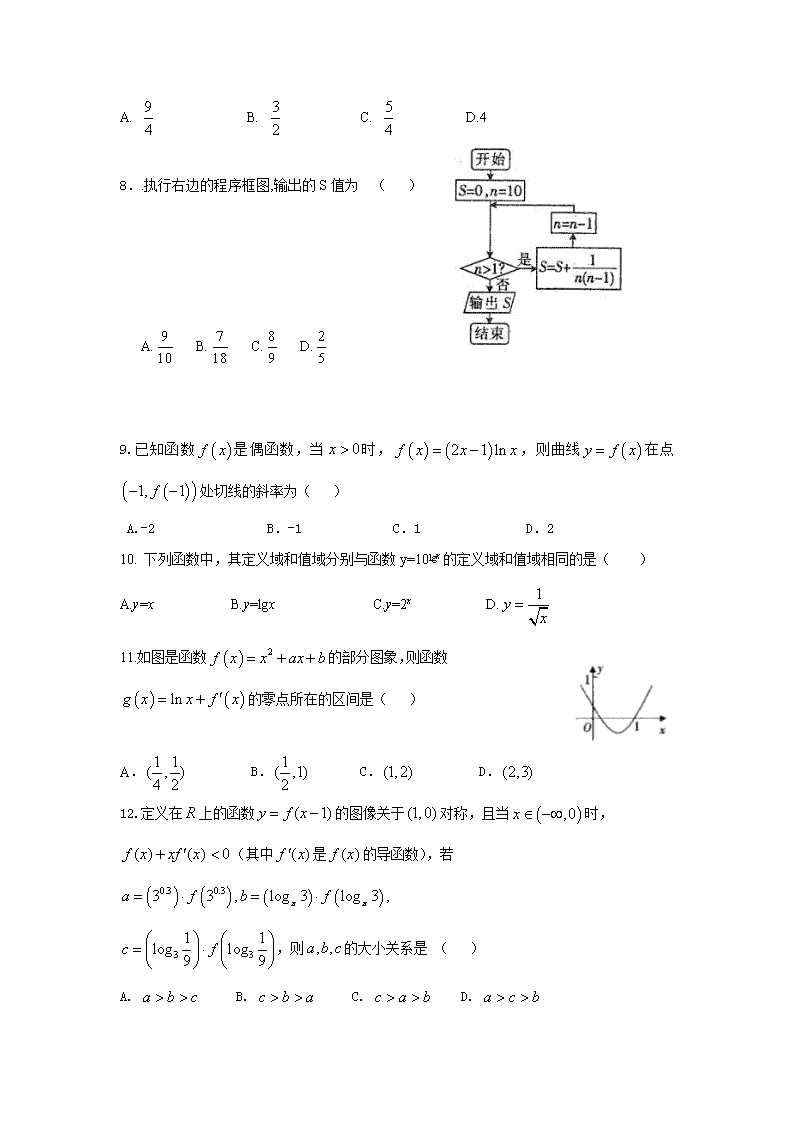
‎2017-2018学年度上学期第一次阶段检测 高三数学试题（文科）‎ ‎ 命题人：大庆市第二十三中学 郝桂欣 一. 选择题：本大题共12小题。每小题5分，在每个小题给出的四个选项中，只有一项是 符合要求的。‎ ‎1．已知集合，则 （ ） ‎ ‎ A． B． C． D． ‎ ‎2．设复数z满足，则=（ ）‎ A． B. C. D.‎ ‎3．函数定义在上.则“曲线过原点”是“为奇函数”的（ ）条件.‎ A．充分而不必要 B．必要而不充分 C．充要 D． 既不充分又不必要 ‎4. 函数的部分图像如图所示，则（ ）‎ ‎（A） （B）‎ ‎（C） （D）‎ ‎5.在△ABC中，AB=1，AC=3，D是BC的中点，则=（ ）‎ ‎ A．3 B．4 C．5 D．不确定 ‎6.已知a＞0，b＞0且ab=1，则函数f（x）=ax与函数g（x）=﹣logbx的图象可能是（ ）‎ ‎7.已知为等差数列的前项和,若,,则的值为( )‎ A. B. C. D.4‎ ‎8．.执行右边的程序框图,输出的S值为 （ ）‎ A. B. C. D.‎ ‎9.已知函数是偶函数，当时，，则曲线在点处切线的斜率为（ ）‎ A.-2 B．-1 C．1 D．2‎ ‎10. 下列函数中，其定义域和值域分别与函数y=10lgx的定义域和值域相同的是（ ）‎ A.y=x B.y=lgx C.y=2x D.‎ ‎11.如图是函数的部分图象，则函数的零点所在的区间是（ ）‎ A． ‎ B． C． D．‎ ‎12.定义在上的函数的图像关于对称，且当时，（其中是的导函数），若 ‎，则的大小关系是 （ ）‎ A. B. C. D. ‎ 二．填空题：共4小题，每小题5分.‎ ‎13. 已知向量a=(m,4)，b=(3,-2)，且a∥b，则m=___________. ‎ ‎14. 若x，y满足约束条件，则的最小值为__________‎ ‎15. △ABC的内角A，B，C的对边分别为a，b，c，若，，a=1，则b=____________.‎ ‎16. 有三张卡片，分别写有1和2，1和3，2和3. 甲，乙，丙三人各取走一张卡片，甲看了乙的卡片后说：“我与乙的卡片上相同的数字不是2”，乙看了丙的卡片后说：“我与丙的卡片上相同的数字不是1”，丙说：“我的卡片上的数字之和不是5”，则甲的卡片上的数字是________________.‎ 三、解答题：解答应写出文字说明，证明过程或演算步骤．‎ ‎17．（本小题满分10分）已知：（为常数）；：代数式有意义．‎ ‎（1）若，求使“”为真命题的实数的取值范围；‎ ‎（2）若是成立的充分不必要条件，求实数的取值范围．‎ ‎18.（本小题满分12分）已知函数 ‎（1）求的最小正周期；‎ ‎（2）求在区间上的最大值和最小值. ‎ ‎19.（本小题满分12分）设数列的前n项和满足.‎ ‎（1）求数列的通项公式；‎ ‎（2）令,求数列的前n项和.‎ ‎20. （本小题满分12分）在中，内角的对边分别为已知． ‎ ‎ （I）求的值； （II）若，，求的面积。‎ ‎21.（本小题满分12分）设函数.‎ ‎（1）求曲线在点处的切线方程；‎ ‎（2）设，若函数有三个不同零点，求的取值范围； ‎ ‎22.（本小题满分12分）已知函数，曲线经过点,且在点处的切线为．‎ ‎（1）求的值；‎ ‎（2）若存在实数，使得时，恒成立，求的取值范围．‎ ‎ 2017——2018学年度上学期第一次阶段检测题 高三数学答案（文科）‎ 一、选择题 1——6 BCBABB 7——12 AABDBC 二、填空题 13、 14、 15、 16、1和3‎ 三、解答题：‎ ‎17. ：等价于：即；‎ ‎：代数式有意义等价于：，即…………2分 ‎（1）时，即为 ‎ 若“”为真命题，则，得：‎ ‎ 故时，使“”为真命题的实数的取值范围是，………5分 ‎（2）记集合，‎ ‎ 若是成立的充分不必要条件，则，……………7分 因此：， ，故实数的取值范围是。……10分 ‎ 18.解：=sin2x+cos2x+2sinxcos x+cos2x=1+sin2x+cos2x ‎=sin(2x+)+1, （4分）‎ 所以函数f(x)的最小正周期为T==。 （6分）‎ ‎ （2）由（1）的计算结果知，= sin(2x+)+1.‎ ‎ 当x时，， （8分）‎ ‎ 由正弦函数在上的图像知，‎ ‎ 当2x+=，即时，取最大值+1；（10分）‎ ‎ 当2x+=，即x=时，取最小值0。 （12分）‎ ‎ 综上，在上的最大值为+1，最小值为0。‎ ‎19.解：（1）∵Sn=2an-2, ∴S1=2a1-2, ∴a1=2, 又Sn-1=2an-1-2（n2）,‎ 两式相减得an=2(an－an-1),即an=2an-1，an=2n …………6分 ‎（2）bn==n,== -,‎ Tn=1-+-+-+-=1-=…………12分 ‎20. 解：（Ⅰ）由正弦定理，得 所以 即,‎ 化简得,即因此 （6分）‎ ‎（Ⅱ）由的 由及 得，解得，因此 又所以，因此 （12分）‎ ‎21.解：（1）由，得.因为，，所以曲线在点处的切线方程为. （4分）‎ ‎（2）当时，，所以.‎ 令，得，解得或. （6分）‎ 与在区间上的变化情况如下表所示.‎ 所以当且时，存在，，，‎ 使得. （10分）‎ 由的单调性，当且仅当时，函数有三个不同零点.（12分）‎ ‎22.解：（1）， （2分）‎ 依题意：，即，解得． （4分）‎ ‎（2）由（1）知，，‎ 由得：，‎ ‎∵时，．‎ ‎∴即恒成立，当且仅当． （6分）‎ 设，，， （8分）‎ 由得（舍去），，‎ 当时，；当时，，‎ ‎∴在区间上的最大值为，（10分）‎ 所以常数的取值范围为．（12分）‎