- 2024-02-26 发布 |
- 37.5 KB |
- 28页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2017年湖北省荆门市中考数学试卷
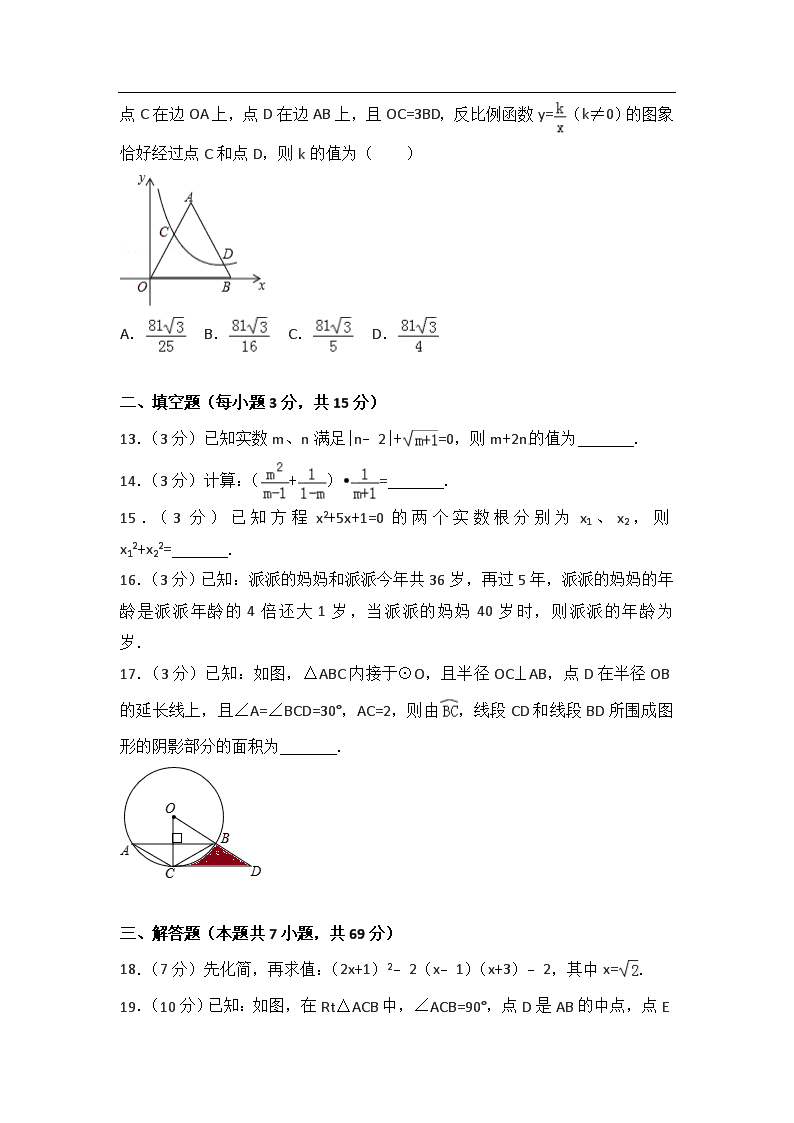
2017年湖北省荆门市中考数学试卷 一、选择题(每小题3分,共36分) 1.(3分)﹣的相反数是( ) A.﹣ B. C. D.﹣ 2.(3分)在函数y=中,自变量x的取值范围是( ) A.x>5 B.x≥5 C.x≠5 D.x<5 3.(3分)在实数﹣、、π、中,是无理数的是( ) A.﹣ B. C.π D. 4.(3分)下列运算正确的是( ) A.4x+5x=9xy B.(﹣m)3•m7=m10 C.(x2y)5=x2y5 D.a12÷a8=a4 5.(3分)已知:如图,AB∥CD,BC平分∠ABD,且∠C=40°,则∠D的度数是( ) A.40° B.80° C.90° D.100° 6.(3分)不等式组的解集为( ) A.x<3 B.x≥2 C.2≤x<3 D.2<x<3 7.(3分)李老师为了了解学生暑期在家的阅读情况,随机调查了20名学生某一天的阅读小时数,具体情况统计如下: 阅读时间 (小时) 2 2.5 3 3.5 4 学生人数(名) 1 2 8 6 3 则关于这20名学生阅读小时数的说法正确的是( ) A.众数是8 B.中位数是3 C.平均数是3 D.方差是0.34 8.(3分)计算:|﹣4|﹣﹣()﹣2的结果是( ) A.2﹣8 B.0 C.﹣2 D.﹣8 9.(3分)一年之中地球与太阳之间的距离随时间而变化,1个天文单位是地球与太阳之间的平均距离,即1.4960亿km,用科学记数法表示1个天文单位是( ) A.14.960×107km B.1.4960×108km C.1.4960×109km D.0.14960×109km 10.(3分)已知:如图,是由若干个大小相同的小正方体所搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是( ) A.6个 B.7个 C.8个 D.9个 11.(3分)在平面直角坐标系xOy中,二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,则下列结论正确的是( ) A.a<0,b<0,c>0 B.﹣=1 C.a+b+c<0 D.关于x的方程ax2+bx+c=﹣1有两个不相等的实数根 12.(3分)已知:如图,在平面直角坐标系xOy中,等边△ AOB的边长为6,点C在边OA上,点D在边AB上,且OC=3BD,反比例函数y=(k≠0)的图象恰好经过点C和点D,则k的值为( ) A. B. C. D. 二、填空题(每小题3分,共15分) 13.(3分)已知实数m、n满足|n﹣2|+=0,则m+2n的值为 . 14.(3分)计算:(+)•= . 15.(3分)已知方程x2+5x+1=0的两个实数根分别为x1、x2,则x12+x22= . 16.(3分)已知:派派的妈妈和派派今年共36岁,再过5年,派派的妈妈的年龄是派派年龄的4倍还大1岁,当派派的妈妈40岁时,则派派的年龄为 岁. 17.(3分)已知:如图,△ABC内接于⊙O,且半径OC⊥AB,点D在半径OB的延长线上,且∠A=∠BCD=30°,AC=2,则由,线段CD和线段BD所围成图形的阴影部分的面积为 . 三、解答题(本题共7小题,共69分) 18.(7分)先化简,再求值:(2x+1)2﹣2(x﹣1)(x+3)﹣2,其中x=. 19.(10分)已知:如图,在Rt△ACB中,∠ ACB=90°,点D是AB的中点,点E是CD的中点,过点C作CF∥AB叫AE的延长线于点F. (1)求证:△ADE≌△FCE; (2)若∠DCF=120°,DE=2,求BC的长. 20.(10分)荆岗中学决定在本校学生中,开展足球、篮球、羽毛球、乒乓球四种活动,为了了解学生对这四种活动的喜爱情况,学校随机调查了该校m名学生,看他们喜爱哪一种活动(每名学生必选一种且只能从这四种活动中选择一种),现将调查的结果绘制成如下不完整的统计图. (1)m= ,n= ; (2)请补全图中的条形图; (3)根据抽样调查的结果,请估算全校1800名学生中,大约有多少人喜爱踢足球; (4)在抽查的m名学生中,喜爱乒乓球的有10名同学(其中有4名女生,包括小红、小梅),现将喜爱打乒乓球的同学平均分成两组进行训练,且女生每组分两人,求小红、小梅能分在同一组的概率. 21.(10分)金桥学校“科技体艺节”期间,八年级数学活动小组的任务是测量学校旗杆AB的高,他们在旗杆正前方台阶上的点C处,测得旗杆顶端A的仰角为45°,朝着旗杆的方向走到台阶下的点F处,测得旗杆顶端A的仰角为60°,已知升旗台的高度BE为1米,点C距地面的高度CD为3米,台阶CF的坡角为30°,且点E、F、D在同一条直线上,求旗杆AB的高度(计算结果精确到0.1米,参考数据:≈1.41,≈1.73) 22.(10分)已知:如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,过点D作DE⊥AD交AB于点E,以AE为直径作⊙O. (1)求证:BC是⊙O的切线; (2)若AC=3,BC=4,求BE的长. 23.(10分)我市雷雷服饰有限公司生产了一款夏季服装,通过实体商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量y1(百件)与时间t(t为整数,单位:天)的部分对应值如下表所示,网上商店的日销售量y2(百件)与时间t(t为整数,单位:天)的部分对应值如图所示. 时间t(天) 0 5 10 15 20 25 30 日销售量 y1(百件) 0 25 40 45 40 25 0 (1)请你在一次函数、二次函数和反比例函数中,选择合适的函数能反映y1与t的变化规律,并求出y1与t的函数关系式及自变量t的取值范围; (2)求y2与t的函数关系式,并写出自变量t的取值范围; (3)在跟踪调查的30天中,设实体商店和网上商店的日销售总量为y(百件),求y与t的函数关系式;当t为何值时,日销售总量y达到最大,并求出此时的最大值. 24.(12分)已知:如图所示,在平面直角坐标系xOy中,∠C=90°,OB=25,OC=20,若点M是边OC上的一个动点(与点O、C不重合),过点M作MN∥OB交BC于点N. (1)求点C的坐标; (2)当△MCN的周长与四边形OMNB的周长相等时,求CM的长; (3)在OB上是否存在点Q,使得△MNQ为等腰直角三角形?若存在,请求出此时MN的长;若不存在,请说明理由. 2017年湖北省荆门市中考数学试卷 参考答案与试题解析 一、选择题(每小题3分,共36分) 1.(3分)(2017•荆门)﹣的相反数是( ) A.﹣ B. C. D.﹣ 【分析】根据相反数的定义求解即可. 【解答】解:﹣的相反数是, 故选:C. 【点评】本题考查了相反数,在一个数的前面加上负号就是这个数的相反数. 2.(3分)(2017•荆门)在函数y=中,自变量x的取值范围是( ) A.x>5 B.x≥5 C.x≠5 D.x<5 【分析】根据二次根式的性质和分式的意义,被开方数大于或等于0,分母不等于0,可以求出x的范围. 【解答】解:要使函数解析式y=有意义, 则x﹣5>0, 解得:x>5, 故选:A. 【点评】本题考查了函数自变量的取值范围,函数自变量的范围一般从三个方面考虑:当函数表达式是整式时,自变量可取全体实数;当函数表达式是分式时,考虑分式的分母不能为0;当函数表达式是二次根式时,被开方数非负. 3.(3分)(2017•荆门)在实数﹣、、π、中,是无理数的是( ) A.﹣ B. C.π D. 【分析】根据无理数、有理数的定义即可判定选择项. 【解答】解:﹣、、是有理数, π是无理数, 故选:C. 【点评】此题主要考查了无理数的定义,注意带根号的要开不尽方才是无理数,无限不循环小数为无理数.如π,,0.8080080008…(每两个8之间依次多1个0)等形式. 4.(3分)(2017•荆门)下列运算正确的是( ) A.4x+5x=9xy B.(﹣m)3•m7=m10 C.(x2y)5=x2y5 D.a12÷a8=a4 【分析】利用同底数幂的乘法和除法及幂的乘方与积的乘方运算即可. 【解答】解:A.4x+5x=9x,所以A错误; B.(﹣m)3•m7=﹣m10,所以B错误; C.(x2y)5=x10y5,所以C错误; D.a12÷a8=a4,所以D正确, 故选D. 【点评】本题主要考查了合并同类项,同底数幂的乘法和除法及幂的乘方与积的乘方运算法则,熟练掌握法则是解答此题的关键. 5.(3分)(2017•荆门)已知:如图,AB∥CD,BC平分∠ABD,且∠C=40°,则∠D的度数是( ) A.40° B.80° C.90° D.100° 【分析】先根据平行线的性质,得出∠ABC的度数,再根据BC平分∠ABD,即可得到∠DBC的度数,最后根据三角形内角和进行计算即可. 【解答】解:∵AB∥CD, ∴∠ABC=∠C=40°, 又∵BC平分∠ABD, ∴∠DBC=∠ABC=40°, ∴△BCD中,∠D=180°﹣40°﹣40°=100°, 故选:D. 【点评】本题主要考查了平行线的性质的运用,解题时注意:两直线平行,内错角相等. 6.(3分)(2017•荆门)不等式组的解集为( ) A.x<3 B.x≥2 C.2≤x<3 D.2<x<3 【分析】先求出每个不等式的解集,再求出不等式组的解集即可. 【解答】解: ∵解不等式①得:x<3, 解不等式②得:x≥2, ∴不等式组的解集为2≤x<3, 故选C. 【点评】本题考查了解一元一次不等式组,能根据不等式的解集求出不等式组的解集是解此题的关键. 7.(3分)(2017•荆门)李老师为了了解学生暑期在家的阅读情况,随机调查了20名学生某一天的阅读小时数,具体情况统计如下: 阅读时间 (小时) 2 2.5 3 3.5 4 学生人数(名) 1 2 8 6 3[来源:学&科&网Z&X&X&K] 则关于这20名学生阅读小时数的说法正确的是( ) A.众数是8 B.中位数是3 C.平均数是3 D.方差是0.34 【分析】A、根据众数的定义找出出现次数最多的数; B、根据中位数的定义将这组数据从小到大重新排列,求出最中间的2个数的平均数,即可得出中位数. C、根据加权平均数公式代入计算可得; D、根据方差公式计算即可. 【解答】解:A、由统计表得:众数为3,不是8,所以此选项不正确; B、随机调查了20名学生,所以中位数是第10个和第11个学生的阅读小时数,都是3,故中位数是3,所以此选项正确; C、平均数==3.35,所以此选项不正确; D、S2=×[(2﹣3.35)2+2(2.5﹣3.35)2+8(3﹣3.35)2+6(3.5﹣3.35)2+3(4﹣3.35)2]==0.2825,所以此选项不正确; 故选B. 【点评】此题考查了众数、中位数、加权平均数、方差,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,众数是一组数据中出现次数最多的数,并熟练掌握平均数和方差公式. 8.(3分)(2017•荆门)计算:|﹣4|﹣﹣()﹣2的结果是( ) A.2﹣8 B.0 C.﹣2 D.﹣8 【分析】本题涉及负指数幂、二次根式化简绝对值3个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果. 【解答】解:原式=4﹣﹣﹣4 =﹣2, 故选:C. 【点评】本题主要考查了实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算. 9.(3分)(2017•荆门)一年之中地球与太阳之间的距离随时间而变化,1个天文单位是地球与太阳之间的平均距离,即1.4960亿km,用科学记数法表示1个天文单位是( ) A.14.960×107km B.1.4960×108km C.1.4960×109km D.0.14960×109km 【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于1时,n是正数;当原数的绝对值小于1时,n是负数. 【解答】解:1.4960亿=1.4960×108, 故选:B. 【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值. 10.(3分)(2017•荆门)已知:如图,是由若干个大小相同的小正方体所搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是( ) A.6个 B.7个 C.8个 D.9个 【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形. 【解答】解:综合三视图可知,这个几何体的底层有4个小正方体,第二层有2个小正方体,第,三层有1个小正方体,因此搭成这个几何体所用小正方体的个数是4+2+1=7个. 故选B. 【点评】本题考查了学生对三视图的掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就更容易得到答案. 11.(3分)(2017•荆门)在平面直角坐标系xOy中,二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,则下列结论正确的是( ) A.a<0,b<0,c>0 B.﹣=1 C.a+b+c<0 D.关于x的方程ax2+bx+c=﹣1有两个不相等的实数根 【分析】根据二次函数的性质一一判断即可. 【解答】解:A、错误.a<0,b>0,c<0. B、错误.﹣>1. C、错误.x=1时,y=a+b+c=0. D、正确.观察图象可知抛物线y=ax2+bx+c与直线y=﹣1有两个交点,所以关于x的方程ax2+bx+c=﹣1有两个不相等的实数根. 故选D. 【点评】本题考查二次函数的性质,二次函数与一元二次方程的关系等知识,解题的关键是读懂图象信息,灵活运用所学知识解决问题. 12.(3分)(2017•荆门)已知:如图,在平面直角坐标系xOy中,等边△AOB的边长为6,点C在边OA上,点D在边AB上,且OC=3BD,反比例函数y=(k≠0)的图象恰好经过点C和点D,则k的值为( ) A. B. C. D. 【分析】过点C作CE⊥x轴于点E,过点D作DF⊥x轴于点F,设BD=a,则OC=3a,根据等边三角形的性质结合解含30度角的直角三角形,可找出点C、D的坐标,再利用反比例函数图象上点的坐标特征即可求出a、k的值,此题得解. 【解答】解:过点C作CE⊥x轴于点E,过点D作DF⊥x轴于点F,如图所示. 设BD=a,则OC=3a. ∵△AOB为边长为6的等边三角形, ∴∠COE=∠DBF=60°,OB=6. 在Rt△COE中,∠COE=60°,∠CEO=90°,OC=3a, ∴∠OCE=30°, ∴OE=a,CE==a, ∴点C(a,a). 同理,可求出点D的坐标为(6﹣a,a). ∵反比例函数y=(k≠0)的图象恰好经过点C和点D, ∴k=a×a=(6﹣a)×a, ∴a=,k=. 故选A. 【点评】本题考查了反比例函数图象上点的坐标特征、等边三角形的性质以及解含30度角的直角三角形,根据等边三角形的性质结合解含30度角的直角三角形,找出点C、D的坐标是解题的关键. 二、填空题(每小题3分,共15分) 13.(3分)(2017•荆门)已知实数m、n满足|n﹣2|+=0,则m+2n的值为 3 . 【分析】根据非负数的性质即可求出m与n的值. 【解答】解:由题意可知:n﹣2=0,m+1=0, ∴m=﹣1,n=2, ∴m+2n=﹣1+4=3, 故答案为:3 【点评】本题考查非负数的性质,解题的关键是求出m与n的值,本题属于基础题型. 14.(3分)(2017•荆门)计算:(+)•= 1 . 【分析】原式括号中两项变形后,利用同分母分式的减法法则计算,约分即可得到结果. 【解答】解:原式=•=•=1. 故答案为:1 【点评】此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键. 15.(3分)(2017•荆门)已知方程x2+5x+1=0的两个实数根分别为x1、x2,则x12+x22= 23 . 【分析】由根与系数的关系可得x1+x2=﹣5、x1•x2=1,将其代入x12+x22=(x1+x2)2﹣2x1•x2中,即可求出结论. 【解答】解:∵方程x2+5x+1=0的两个实数根分别为x1、x2, ∴x1+x2=﹣5,x1•x2=1, ∴x12+x22=(x1+x2)2﹣2x1•x2=(﹣5)2﹣2×1=23. 故答案为:23. 【点评】本题考查了根与系数的关系,牢记两根之和等于﹣、两根之积等于是解题的关键. 16.(3分)(2017•荆门)已知:派派的妈妈和派派今年共36岁,再过5年,派派的妈妈的年龄是派派年龄的4倍还大1岁,当派派的妈妈40岁时,则派派的年龄为 12 岁. 【分析】设今年派派的年龄为x岁,则妈妈的年龄为(36﹣x)岁,根据再过5年派派的妈妈的年龄是派派年龄的4倍还大1岁,即可得出关于x的一元一次方程,解之即可得出x的值,将其代入36﹣x﹣x中可求出二者的年龄差,再用40减去该年龄差即可求出当派派的妈妈40岁时派派的年龄. 【解答】解:设今年派派的年龄为x岁,则妈妈的年龄为(36﹣x)岁, 根据题意得:36﹣x+5=4(x+5)+1, 解得:x=4, ∴36﹣x﹣x=28, ∴40﹣28=12(岁). 故答案为:12. 【点评】本题考查了一元一次方程的应用,根据再过5年派派的妈妈的年龄是派派年龄的4倍还大1岁,列出关于x的一元一次方程是解题的关键. 17.(3分)(2017•荆门)已知:如图,△ABC内接于⊙O,且半径OC⊥AB,点D在半径OB的延长线上,且∠A=∠BCD=30°,AC=2,则由,线段CD和线段BD所围成图形的阴影部分的面积为 2﹣π . 【分析】根据圆周角定理和垂径定理得到∠O=60°,=,根据等腰三角形的性质得到∠ABC=∠A=30°,得到∠OCB=60°,解直角三角形得到CD=OC=2,于是得到结论. 【解答】解:∵OC⊥AB,∠A=∠BCD=30°,AC=2, ∴∠O=60°,=, ∴AC=BC=6, ∴∠ABC=∠A=30°, ∴∠OCB=60°, ∴∠OCD=90°, ∴OC=BC=2, ∴CD=OC=2, ∴线段CD和线段BD所围成图形的阴影部分的面积=S△OCD﹣S扇形BOC﹣2×2﹣=2﹣π, 故答案为:2﹣π. 【点评】本题考查了扇形的面积的计算,圆周角定理,垂径定理,等边三角形的判定和性质,正确的识别图形是解题的关键. 三、解答题(本题共7小题,共69分) 18.(7分)(2017•荆门)先化简,再求值:(2x+1)2﹣2(x﹣1)(x+ 3)﹣2,其中x=. 【分析】原式利用完全平方公式,多项式乘以多项式法则计算,去括号合并得到最简结果,把x的值代入计算即可求出值. 【解答】解:原式=4x2+4x+1﹣2x2﹣4x+6﹣2=2x2+5, 当x=时,原式=4+5=9. 【点评】此题考查了整式的混合运算﹣化简求值,熟练掌握运算法则是解本题的关键. 19.(10分)(2017•荆门)已知:如图,在Rt△ACB中,∠ACB=90°,点D是AB的中点,点E是CD的中点,过点C作CF∥AB叫AE的延长线于点F. (1)求证:△ADE≌△FCE; (2)若∠DCF=120°,DE=2,求BC的长. 【分析】(1)先根据点E是CD的中点得出DE=CE,再由AB∥CF可知∠BAF=∠AFC,根据AAS定理可得出△ADE≌△FCE; (2)根据直角三角形的性质可得出AD=CD=AB,再由AB∥CF可知∠BDC=180°﹣∠DCF=180°﹣120°=60°,由三角形外角的性质可得出∠DAC=∠ACD=∠BDC=30°,进而可得出结论. 【解答】(1)证明:∵点E是CD的中点, ∴DE=CE. ∵AB∥CF, ∴∠BAF=∠AFC. 在△ADE与△FCE中, ∵, ∴△ADE≌△FCE(AAS); (2)解:由(1)得,CD=2DE, ∵DE=2, ∴CD=4. ∵点D为AB的中点,∠ACB=90°, ∴AB=2CD=8,AD=CD=AB. ∵AB∥CF, ∴∠BDC=180°﹣∠DCF=180°﹣120°=60°, ∴∠DAC=∠ACD=∠BDC=×60°=30°, ∴BC=AB=×8=4. 【点评】本题考查的是全等三角形的判定与性质,熟知全等三角形的判定定理是解答此题的关键. 20.(10分)(2017•荆门)荆岗中学决定在本校学生中,开展足球、篮球、羽毛球、乒乓球四种活动,为了了解学生对这四种活动的喜爱情况,学校随机调查了该校m名学生,看他们喜爱哪一种活动(每名学生必选一种且只能从这四种活动中选择一种),现将调查的结果绘制成如下不完整的统计图. (1)m= 100 ,n= 15 ; (2)请补全图中的条形图; (3)根据抽样调查的结果,请估算全校1800名学生中,大约有多少人喜爱踢足球; (4)在抽查的m名学生中,喜爱乒乓球的有10名同学(其中有4名女生,包括小红、小梅),现将喜爱打乒乓球的同学平均分成两组进行训练,且女生每组分两人,求小红、小梅能分在同一组的概率. 【分析】(1)根据喜爱乒乓球的有10人,占10%可以求得m的值,从而可以求得n的值; (2)根据题意和m的值可以求得喜爱篮球的人数,从而可以将条形统计图补充完整; (3)根据统计图中的数据可以估算出全校1800名学生中,大约有多少人喜爱踢足球; (4)根据题意可以写出所有的可能性,注意(C,D)和(D,C)在一起都是暗含着(A,B)在一起. 【解答】解:(1)由题意可得, m=10÷10%=100,n%=15÷100=15%, 故答案为:100,15; (2)喜爱篮球的有:100×35%=35(人), 补全的条形统计图,如右图所示; (3)由题意可得, 全校1800名学生中,喜爱踢足球的有:1800×=720(人), 答:全校1800名学生中,大约有720人喜爱踢足球; (4)设四名女生分别为:A(小红)、B(小梅)、C、D,[来源:Z&xx&k.Com] 则出现的所有可能性是: (A,B)、(A,C)、(A,D)、 (B,A)、(B,C)、(B,D)、 (C,A)、(C,B)、(C,D)、 (D,A)、(D,B)、(D,C), ∴小红、小梅能分在同一组的概率是:. 【点评】本替考查列表法与树状图法、扇形统计图、条形统计图、用样本估计总体,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答. 21.(10分)(2017•荆门)金桥学校“科技体艺节”期间,八年级数学活动小组的任务是测量学校旗杆AB的高,他们在旗杆正前方台阶上的点C处,测得旗杆顶端A的仰角为45°,朝着旗杆的方向走到台阶下的点F处,测得旗杆顶端A的仰角为60°,已知升旗台的高度BE为1米,点C距地面的高度CD为3米,台阶CF的坡角为30°,且点E、F、D在同一条直线上,求旗杆AB的高度(计算结果精确到0.1米,参考数据:≈1.41,≈1.73) 【分析】过点C作CM⊥AB于M.则四边形MEDC是矩形,设EF=x,根据AM=DE,列出方程即可解决问题. 【解答】解:过点C作CM⊥AB于M.则四边形MEDC是矩形, ∴ME=DC=3.CM=ED, 在Rt△AEF中,∠AFE=60°,设EF=x,则AF=2x,AE=x, 在Rt△FCD中,CD=3,∠CFD=30°, ∴DF=3, 在Rt△AMC中,∠ACM=45°, ∴∠MAC=∠ACM=45°, ∴MA=MC, ∵ED=CM, ∴AM=ED, ∵AM=AE﹣ME,ED=EF+DF, ∴x﹣3=x+3, ∴x=6+3, ∴AE=(6+3)=6+9, ∴AB=AE﹣BE=9+6﹣1≈18.4米. 答:旗杆AB的高度约为18.4米. 【点评】本题考查解直角三角形﹣仰角俯角问题,坡度坡角问题等知识,解题的关键是学会利用参数,构建方程解决问题,属于中考常考题型. 22.(10分)(2017•荆门)已知:如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,过点D作DE⊥AD交AB于点E,以AE为直径作⊙O. (1)求证:BC是⊙O的切线; (2)若AC=3,BC=4,求BE的长. 【分析】(1)连接OD,由AE为直径、DE⊥AD可得出点D在⊙O上且∠DAO=∠ADO,根据AD平分∠CAB可得出∠CAD=∠DAO=∠ADO,由“内错角相等,两直线平行”可得出AC∥DO,再结合∠C=90°即可得出∠ODB=90°,进而即可证出BC是⊙O的切线; (2)在Rt△ACB中,利用勾股定理可求出AB的长度,设OD=r,则BO=5﹣r,由OD∥AC可得出=,代入数据即可求出r值,再根据BE=AB﹣AE即可求出BE的长度. 【解答】(1)证明:连接OD,如图所示. 在Rt△ADE中,点O为AE的中心, ∴DO=AO=EO=AE, ∴点D在⊙O上,且∠DAO=∠ADO. 又∵AD平分∠CAB, ∴∠CAD=∠DAO, ∴∠ADO=∠CAD, ∴AC∥DO. ∵∠C=90°, ∴∠ODB=90°,即OD⊥BC. 又∵OD为半径, ∴BC是⊙O的切线; (2)解:∵在Rt△ACB中,AC=3,BC=4, ∴AB=5. 设OD=r,则BO=5﹣r. ∵OD∥AC, ∴△BDO∽△BCA, ∴=,即=, 解得:r=, ∴BE=AB﹣AE=5﹣=. 【点评】本题考查了切线的判定与性质、相似三角形的判定与性质、平行线的判定与性质以及勾股定理,解题的关键是:(1)利用平行线的性质找出OD⊥BC;(2)利用相似三角形的性质求出⊙O的半径. 23.(10分)(2017•荆门)我市雷雷服饰有限公司生产了一款夏季服装,通过实体商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量y1(百件)与时间t(t为整数,单位:天)的部分对应值如下表所示,网上商店的日销售量y2(百件)与时间t(t为整数,单位:天)的部分对应值如图所示. 时间t(天) 0 5 10 15 20 25 30 日销售量 y1(百件)[来源:学科网ZXXK] 0 25 40 45 40 25 0 (1)请你在一次函数、二次函数和反比例函数中,选择合适的函数能反映y1与t的变化规律,并求出y1与t的函数关系式及自变量t的取值范围; (2)求y2与t的函数关系式,并写出自变量t的取值范围; (3)在跟踪调查的30天中,设实体商店和网上商店的日销售总量为y(百件),求y与t的函数关系式;当t为何值时,日销售总量y达到最大,并求出此时的最大值. 【分析】(1)根据观察可设y1=at2+bt+c,将(0,0),(5,25),(10,40)代入即可得到结论; (2)当0≤t≤10时,设y2=kt,求得y2与t的函数关系式为:y2=4t,当10≤t≤30时,设y2=mt+n,将(10,40),(30,60)代入得到y2与t的函数关系式为:y2=k+30, (3)依题意得y=y1+y2,当0≤t≤10时,得到y最大=80;当10<t≤30时,得到y最大=91.2,于是得到结论. 【解答】解(1)根据观察可设y1=at2+bt+c,将(0,0),(5,25),(10,40)代入得:, 解得, ∴y1与t的函数关系式为:y1=﹣t2+6t(0≤t≤30,且为整数); (2)当0≤t≤10时,设y2=kt, ∵(10,40)在其图象上, ∴10k=40, ∴k=4, ∴y2与t的函数关系式为:y2=4t, 当10≤t≤30时,设y2=mt+n, 将(10,40),(30,60)代入得,解得, ∴y2与t的函数关系式为:y2=k+30, 综上所述,y2=; (3)依题意得y=y1+y2,当0≤t≤10时,y=﹣t2+6t+4t=﹣t2+10t=﹣(t﹣25)2+125, ∴t=10时,y最大=80; 当10<t≤30时,y=﹣t2+6t+t+30=﹣t2+7t+30=﹣(t﹣)2+, ∵t为整数, ∴t=17或18时,y最大=91.2, ∵91.2>80, ∴当t=17或18时,y最大=91.2(百件). 【点评】本题考查了二次函数的应用,一次函数的应用,待定系数法求函数的解析式,正确的理解题意是解题的关键. 24.(12分)(2017•荆门)已知:如图所示,在平面直角坐标系xOy中,∠C=90°,OB=25,OC=20,若点M是边OC上的一个动点(与点O、C不重合),过点M作MN∥OB交BC于点N. (1)求点C的坐标; (2)当△MCN的周长与四边形OMNB的周长相等时,求CM的长; (3)在OB上是否存在点Q,使得△MNQ为等腰直角三角形?若存在,请求出此时MN的长;若不存在,请说明理由. 【分析】(1)如图1,过C作CH⊥OB于H,根据勾股定理得到BC== =15,根据三角形的面积公式得到CH===12,由勾股定理得到OH==16,于是得到结论;[来源:学科网ZXXK] (2)∵根据相似三角形的性质得到===,设CM=x,则CN=x,根据已知条件列方程即可得到结论; (3)如图2,由(2)知,当CM=x,则CN=x,MN=x,①当∠OMQ1=90°MN=MQ时,②当∠MNQ2=90°,MN=NQ2时,根据相似三角形的性质即可得到结论. 【解答】解:(1)如图1,过C作CH⊥OB于H, ∵∠C=90°,OB=25,OC=20, ∴BC===15, ∵S△OBC=OB•CH=OC•BC, ∴CH===12, ∴OH==16, ∴C(16,﹣12);[来源:Zxxk.Com] (2)∵MN∥OB, ∴△CNM∽△COB, ∴===, 设CM=x,则CN=x, ∵△MCN的周长与四边形OMNB的周长相等, ∴CM+CN+MN=OM+MN+OB,即x+x+MN=20﹣x+mn+15﹣x+25, 解得:x=, ∴CM=; (3)如图2,由(2)知,当CM=x,则CN=x,MN=x, ①当∠OMQ1=90°MN=MQ时, ∵△OMQ∽△OBC, ∴=, ∵MN=MQ, ∴=, ∴x=, ∴MN=x=×=; ②当∠MNQ2=90°,MN=NQ2时, 此时,四边形MNQ2Q1是正方形, ∴NQ2=MQ1=MN, ∴MN=. ③当∠MQN=90°,MQ=NQ时, 过M作MH⊥OB于H,∵MN=MQ,MQ=MH,∴MN=2MH,∴MH=x,∵△OMH∽△OBC,∴=,∴x=,∴MN=x=. 【点评】本题考查了相似三角形的判定和性质,正方形的判定和性质,勾股定理,三角形面积公式,正确的作出辅助线是解题的关键. 查看更多