数学理卷·2019届山东省桓台第二中学高二12月月考（2017-12）

数学理卷·2019届山东省桓台第二中学高二12月月考（2017-12）

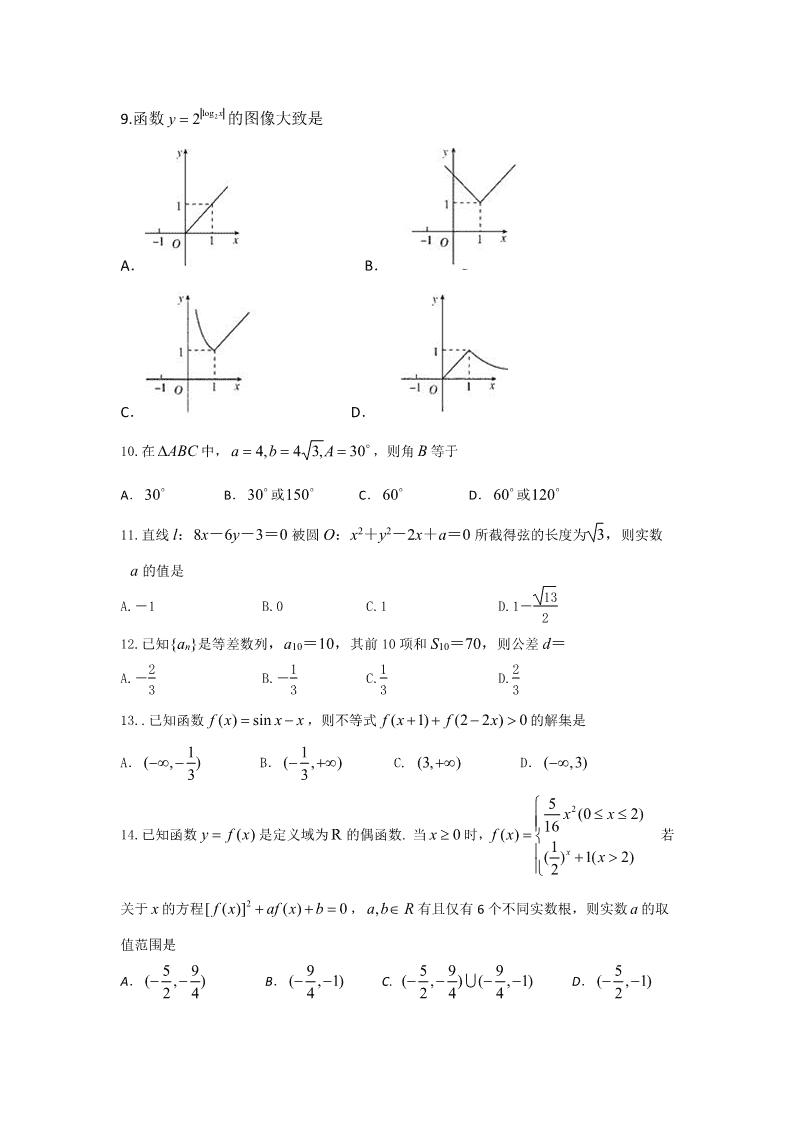
高二阶段性检测理科数学试题 一、选择题：本题共 14 小题，每小题 5 分，共 70 分。在每小题给出的四个选项中，只有 一项是符合题目要求的。 1．已知全集 {1,2,3,4,5}U  ，集合 {1,2,3}A  ， {3,4,5}B  ，则 UA B ð A．{3} B．{1,2,4,5} C．{1,2} D．{1,3,5} 2．复数 i2 5 （ i 是虚数单位）的共轭复数．．．．是 A． i2 B． i2 C． i 2 D． i 2 3.函数 1( ) lg(1 )1f x xx    的定义域是 A. ( , 1)  B.(1，+  ） C. ( 1,1) (1, )  D.（-  ，+  ） 4.为了得到函数 y=sin（2x- 3  ）（XR）的图像，只需把函数 y=sin2x 的图像上所有的点 A.向右平移 3  个单位长度 B.向右平移 6  个单位长度 C.向左平移 3  个单位长度 D.向左平移 6  个单位长度 5.设向量  2,1 a ，向量  4,3b ，向量  2,3c ，则向量    cba 2 （ ） A．（－15，12） B.0 C.－3 D.－11 6．已知实数 ,x y 满足 2 0 1 0, 2 1 0 x y x y z x y x y             则 的最大值为（ ） A. 2 B. 1 C.0 D.4 7.一个几何体的三视图如图所示，则该几何体的体积为 A.2π B.4π C.6π D.12π 8．执行如图所示的程序框图，则输出 s 的值为 A.3 4 B.5 6 C.11 12 D.25 24 9.函数 2log2 xy  的图像大致是 A． B． C． D． 10.在 ABC 中， 30,34,4  Aba ，则角 B 等于 A． 30 B． 30 或 150 C． 60 D． 60 或 120 11.直线 l：8x－6y－3＝0 被圆 O：x2＋y2－2x＋a＝0 所截得弦的长度为 3，则实数 a 的值是 A.－1 B.0 C.1 D.1－ 13 2 12.已知{an}是等差数列，a10＝10，其前 10 项和 S10＝70，则公差 d＝ A.－2 3 B.－1 3 C.1 3 D.2 3 13..已知函数 ( ) sinf x x x  ，则不等式 ( 1) (2 2 ) 0f x f x    的解集是 A． 1( , )3   B． 1( , )3   C. (3, ) D． ( ,3) 14.已知函数 ( )y f x 是定义域为 R 的偶函数. 当 0x  时， 25 (0 2)16( ) 1( ) 1( 2)2 x x x f x x        若 关于 x 的方程 2[ ( )] ( ) 0f x af x b   ， ,a b R 有且仅有 6 个不同实数根，则实数 a 的取 值范围是 A． 5 9( , )2 4   B． 9( , 1)4   C. 5 9 9( , ) ( , 1)2 4 4     D． 5( , 1)2   二．填空题：本题共 6 小题，每小题 5 分,共 30 分. 15.已知函数 2 1, 0( ) 1 , 0 x xf x x x       ，则 ( ( 3))f f   ． 16．若 1sin( )4 3    ，则 cos( 2 )2    ____________. 17.在区间[－2，4]上随机地取一个数 x，若 x 满足|x|≤m 的概率为5 6 ，则 m＝________. 18.已知 a＞0，b＞0，a＋b＝1，则 y＝1 a ＋4 b 的最小值是 19.已知某商场新进 3 000 袋奶粉，为检查其三聚氰胺是否达标，现采用系统抽样的方法从中 抽取 150 袋检查，若第一组抽出的号码是 11，则 6 组抽出的号码为________. 20.如果对定义在区间 D 上的函数  f x ，对区间 D 内任意两个不相等的实数 1 2,x x ，都有        1 1 2 2 1 2 2 1x f x x f x x f x x f x   ，则称函数  f x 为区间 D 上的“ H 函数”，给出 下列函数及函数对应的区间： ①    3 21 1 1 ,3 2 2f x x x x x    R ； ②   π3 cos sin , 0, 2f x x x x x         ； ③      1 e , ,1xf x x x    ； ④   1ln , 0, ef x x x x      ； 以上函数为区间 D 上的“ H 函数”的序号是__________．（写出所有正确的序号） 三．解答题：共 50 分. 21.（12 分）设等差数列{an}的前 n 项和为 Sn，且 S3＝2S2＋4，a5＝36. (1)求 an，Sn； (2)设 bn＝Sn－1(n∈N*)，Tn＝ 1 b1 ＋ 1 b2 ＋ 1 b3 ＋…＋ 1 bn ，求 Tn. 22.（12 分）已知函数 Rxxxxxf  ,2 12coscossin3)( . (1)求函数 )(xf 的最小值和最小正周期. (2) 已 知 △ ABC 内 角 A,B,C 的 对 边 分 别 为 a,b,c, 且 c=3,f(C)=0, 若 向 量 )sin,1( Am  与 )sin2( Bn ， 共线,求 a,b 的值. 23.（12 分）如图所示，在四棱锥 P－ABCD 中，平面 PAD⊥平面 ABCD， AB＝AD，∠BAD＝60°，E，F 分别是 AP，AD 的中点. 求证：(1)直线 EF∥平面 PCD； (2)平面 BEF⊥平面 PAD. 24.（14 分） 已知函数 1)( 2   x baxxf 是定义在（-1,1）的奇函数，且 5 2)2 1( f （1）求 f(x)解析式 （2）用定义证明 f(x)在（-1,1）上是增函数 （3）解不等式 0)()1(  tftf 高二阶段性检测理科数学试题答案 1-5:CBCDC 6-10:DCDCD 11-14：BDCC 15.5 16. 17. 3 18. 9 19.111 20. （1）（2） 21.解 (1)因为 S3＝2S2＋4，所以 a1－d＝－4， 又因为 a5＝36，所以 a1＋4d＝36. 解得 d＝8，a1＝4，所以 an＝4＋8(n－1)＝8n－4，Sn＝n（4＋8n－4） 2 ＝4n2. (2)bn＝4n2－1＝(2n－1)(2n＋1)， 所以 1 bn＝ 1（2n－1）（2n＋1）＝1 2 1 2n＋1. Tn＝ 1 b1＋ 1 b2＋ 1 b3＋…＋ 1 bn＝1 2 1 2n＋1 ＝1 2 1 2n＋1＝ n 2n＋1. 22. 解 1)f(x)= sinxcosx-cos2x- = sin2x- cos2x-1=sin -1 . 所以 f(x)的最小值为-2,最小正周期为π. (2)因为 f(C)=sin -1=0,即 sin =1, 又因为 00，(x1x2-1)<0 所以：f(x1)-f(x2)<0 f(x1)

查看更多