云南省玉溪市2013年高三复习检测--数学（文）

云南省玉溪市2013年高三复习检测--数学（文）

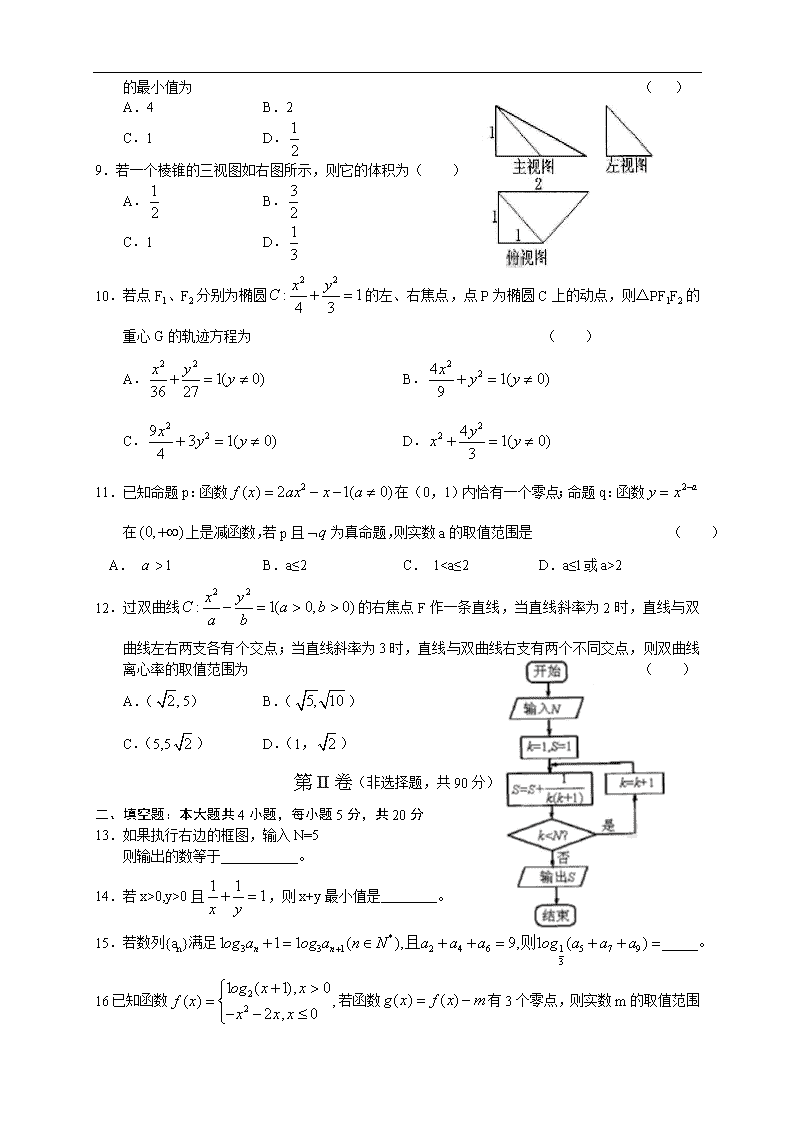
云南省玉溪市 ‎2013年高中毕业班复习检测 数学（文）试题 第Ⅰ卷（选择题，共60分）‎ 一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．若集合则等于 ‎ A．（－1，2） B．（0，2） C． D．（2，）‎ ‎2．复数为虚数单位）的虚部是 ‎ ‎ A． B． C．－ D．－‎ ‎3．已知等差数列{an}的公差为2，若a1，a3，a4成等比数列，那么a2= ‎ ‎ A．－6 B．－‎8 ‎ C．8 D． 6‎ ‎4．某学校从高三全体500名学生中抽50名学生作学习状况问卷调查，现将500名学生从1到500进行编号，求得间隔数，即每10人抽取一个人，在1～10中随机抽取一个数，如果抽到的是6，则从125～140的数中应抽取的数是 （ ）‎ ‎ A．126 B．‎136 ‎C．146 D．126和136‎ ‎5．若向量 ‎ A． B． C． D．‎ ‎6．设不等式表示的平面区域与抛物线的准线围成的三角形区域（包含边界）为D，P（x，y）为D内的一个动点，则目标函数z=x-2y+5的最大值为 （ ）‎ ‎ A．4 B．‎5 ‎C．8 D．12‎ ‎7．已知一个球与一个正三棱柱的三个侧面和两个底面都相切，若这个球的体积是 ，则这个三棱柱的体积是 （ ）‎ ‎ A． B．‎16‎ C．24 D．48‎ ‎8．设函数，若对于任意都有成立，则|x1－x2‎ ‎|的最小值为 （ ）‎ ‎ A．4 B．2 ‎ ‎ C．1 D．‎ ‎9．若一个棱锥的三视图如右图所示，则它的体积为（ ）‎ ‎ A． B． ‎ ‎ C．1 D．‎ ‎10．若点F1、F2分别为椭圆的左、右焦点，点P为椭圆C上的动点，则△PF‎1F2的重心G的轨迹方程为 （ ）‎ ‎ A． B．‎ ‎ C． D．‎ ‎11．已知命题p：函数在（0，1）内恰有一个零点；命题q：函数在上是减函数，若p且为真命题，则实数a的取值范围是 （ ）‎ ‎ A． B．a≤‎2 ‎ C． 12‎ ‎12．过双曲线的右焦点F作一条直线，当直线斜率为2时，直线与双曲线左右两支各有个交点；当直线斜率为3时，直线与双曲线右支有两个不同交点，则双曲线离心率的取值范围为 （ ）‎ ‎ A．（5） B．（） ‎ ‎ C．（5,5） D．（1，）‎ 第II卷（非选择题，共90分）‎ 二、填空题：本大题共4小题，每小题5分，共20分 ‎13．如果执行右边的框图，输入N=5‎ ‎ 则输出的数等于 。‎ ‎14．若x>0,y>0且，则x+y最小值是 。‎ ‎15．若数列{an}满足 。‎ ‎16已知函数若函数有3个零点，则实数m的取值范围 是____．‎ 三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤．‎ ‎17．（本小题满分12分）‎ ‎ 在△ABC中，内角A、B、C的对边分别为a、b、c, a2 +b2 =4abcosC，且。‎ ‎ （I）求角C的大小：‎ ‎ （II）设函数，且直线与函数图象相邻两交点间的距离为，求f （A）的取值范围。‎ ‎18．（本小题满分l2分）‎ ‎ 某学校制定学校发展规划时，对现有教师进行年龄状况和接受教育程度（学历）的调查，其结果（人数分布）如表：‎ 学历 ‎35岁以下 ‎35～50岁 ‎50岁以上 本科 ‎80‎ ‎30‎ ‎20‎ 研究生 x ‎20‎ y ‎ （Ⅰ）用分层抽样的方法在35～50岁年龄段的教师中抽取一个容量为5的样本，将该样本看成一个总体，从中任取2人，求至少有1人的学历为研究生的概率；‎ ‎ （Ⅱ）在该校教师中按年龄状况用分层抽样的方法抽取N个人，其中35岁以下48人，50岁以上10人，再从这N个人中随机抽取1人，此人的年龄为50岁以上的概率为，求x、y的值。‎ ‎19．（本小题满分12分）‎ ‎ 如图，在四棱锥 P— ABCD中，底面ABCD为矩形，PD ⊥底面ABCD，E是AB上一点，PD=，CD=4，AD=． ‎ ‎ （Ⅰ）若∠ADE=，求证：CE⊥平面PDE；‎ ‎ （Ⅱ）当点A到平面PDE的距离为时，‎ ‎ 求三棱锥A— PDE的侧面积。‎ ‎20．（本小题满分12分）‎ ‎ 已知A，B分别为椭圆的左、右顶点，F为椭圆的右焦点，AF=3·FB，若椭圆上的点C在AB上的射影恰为F，日△ABC的面积为3．‎ ‎ （I）求椭圆的方程；‎ ‎ （II）设P为直线x=4上不同于点（4，0）的任意一点，若直线AP，BP分别与椭圆交于点A，M和点B，N，证明点B在以MN为直径的圆内。‎ ‎21．（本小题满分12分）‎ ‎ 已知函数图象上点处的切线方程为2x－y－3=0。‎ ‎ （Ⅰ）求函数的解析式；‎ ‎ （Ⅱ）若函数在上恰有两个零点，求实数m的取值范围．‎ 选考题（本小题满分10分）‎ ‎ 请考生在第22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分．做答时，用2B铅笔在答题卡上把所选题目对应的题号涂黑．‎ ‎22．（本小题满分10分）选修4 —1：几何证明选讲 ‎ 如图，△ABC内接于⊙O，AB=AC，直线MN切⊙O于点C，‎ 弦BD∥MN，AC与BD相交于点E。‎ ‎ （I）求证△ABE≌△ACD；‎ ‎ （II）若AB=6，BC =4，求线段AE的长。‎ ‎23．（本小题满分10分）选修4—4：坐标系与参数方程 ‎ 在平面直角坐标系xOy中，过点P（l,0）作倾斜角为的直线，以原点O为极点，x轴非负半轴为极轴建立极坐标系，曲线C1的极坐标方程为p=l，将曲线C1上各点的横坐标伸长为原来的2倍，纵坐标不变，得到曲线C2，直线与曲线C2交于不同的两点M，N ‎ （Ⅰ）求曲线C2的普通方程；‎ ‎ （Ⅱ）求的值。‎ ‎24．（本小题满分10分）选修4—5：不等式选讲 ‎ 设函数。‎ ‎ （Ⅰ）若a=l，解不等式 ‎ （II）若函数f （x）有最小值，求实数a的取值范围。‎