2020学年高二数学下学期期末考试试题 文新人教目标版

2020学年高二数学下学期期末考试试题 文新人教目标版

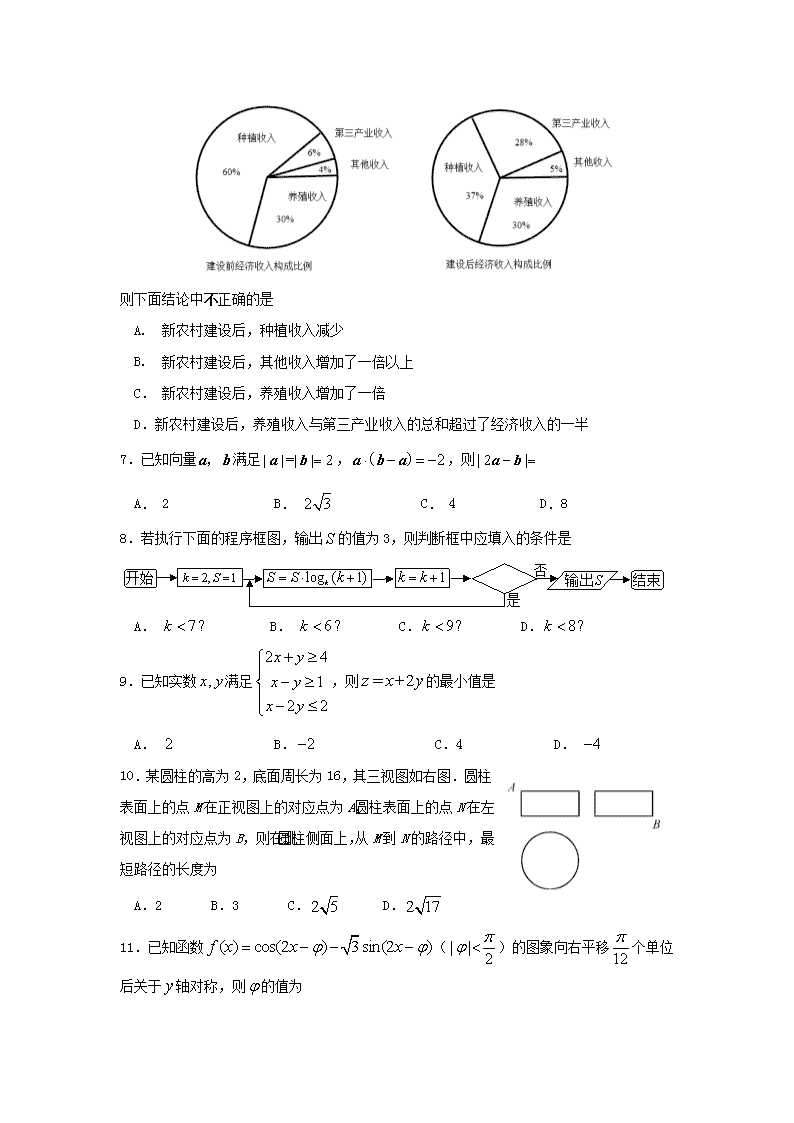
‎2019-2学期高二年级期末考试试题 数 学（文）‎ 说明：本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分，考试时间120分钟．答案写在答题卡上，交卷时只交答题卡．‎ 第Ⅰ卷（选择题，共60分）‎ 一、 选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．直线x－y＋3＝0的倾斜角为 ‎ A．30° B． 60° C． 120° D．150°‎ ‎2．设集合，集合，则 A． B． C． D． ‎ ‎3．等差数列的前项和为，且满足，则 A． B． C． D． ‎ ‎4．若命题“∃R，使得”是真命题，则实数a的取值范围是 A．(－1，3) B．[－1，3] C． D． ‎ ‎5. 已知，，，则、、的大小关系是 A． B． C． D．‎ ‎6．某地区经过一年的新农村建设，农村的经济收入增加了一倍，实现翻番．为更好地了解该地区农村的经济收入变化情况，统计了该地区新农村建设前后农村的经济收入构成比例，得到如下饼图：‎ ‎ ‎ 则下面结论中不正确的是 ‎　A. 新农村建设后，种植收入减少 ‎　B. 新农村建设后，其他收入增加了一倍以上 ‎　C． 新农村建设后，养殖收入增加了一倍 ‎　D．新农村建设后，养殖收入与第三产业收入的总和超过了经济收入的一半 ‎7．已知向量满足，，则 ‎　A． 2　 B． C． 4 D．8‎ ‎8．若执行下面的程序框图，输出的值为3，则判断框中应填入的条件是 A． B． C． D． ‎ ‎9．已知实数满足，则的最小值是 ‎　A． 　 B． C．4 D． ‎ ‎10．某圆柱的高为2，底面周长为16，其三视图如右图．圆柱表面上的点M在正视图上的对应点为A，圆柱表面上的点N在左视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中，最短路径的长度为 A．2 B．3 C． D． ‎ ‎11．已知函数（）的图象向右平移个单位后关于轴对称，则的值为 A． B． C． D．‎ 12． 已知函数，则不等式的解集为 ‎ A． B． C． D．‎ 第Ⅱ卷（非选择题，共90分）‎ 二、填空题：本大题共4小题，每小题5分，共20分.‎ ‎13．已知，则的最小值是 ．‎ ‎14．若直线与直线平行，则实数的值为 ‎ ‎ ．‎ ‎15．已知定义在实数集R上的偶函数在区间上是减函数，则不等式 的解集是 ．‎ ‎16．半径为4的球的球面上有四点A,B,C,D，已知为等边三角形且其面积为，则三棱锥体积的最大值为 ．‎ 三、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤. ‎ ‎17．（本小题10分）‎ 已知在等比数列中，，且是和的等差中项．‎ ‎（Ⅰ）求数列的通项公式；‎ ‎（Ⅱ）若数列满足，求数列的前n项和．‎ 18． ‎（本小题12分）‎ 已知函数．‎ ‎（Ⅰ）求的最小正周期和单调递增区间；‎ ‎（Ⅱ）求在区间上的最大值及取得最大值时x的值．‎ 18． ‎（本小题12分）‎ 在中，角所对的边分别为，已知.‎ ‎（Ⅰ）求角；‎ ‎（Ⅱ）若点在边上，且，的面积为，求.‎ 19． ‎（本小题12分）‎ 某校高三课外兴趣小组为了解高三同学高考结束后是否打算观看2018年足球世界杯比赛的情况,从全校高三年级1500名男生、1000名女生中按分层抽样的方式抽取125名学生进行问卷调查,情况如下表:‎ 打算观看 不打算观看 女生 ‎20‎ m 男生 n ‎ ‎25‎ ‎（Ⅰ）求出表中数据m，n；‎ ‎（Ⅱ）判断是否有99%的把握认为观看2018年足球世界杯比赛与性别有关；‎ ‎（Ⅲ）)为了计算“从10人中选出9人参加比赛”的情况有多少种，我们可以发现：它与“从10人中选出1人不参加比赛”的情况有多少种是一致的.现有问题：在打算观看2018年足球世界杯比赛的同学中有5名男生、2名女生来自高三（5）班，从中推选5人接受校园电视台采访，请根据上述方法，求被推选出的5人中恰有四名男生、一名女生的概率. ‎ P(K2≥k0)‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.01‎ ‎0.005‎ K0 ‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ 附：‎ 20． ‎（本小题12分）‎ 如图，在四棱锥中，底面为正方形，,. ‎ ‎（Ⅰ）若是的中点，‎ 求证：∥平面；‎ ‎（Ⅱ）若，，‎ 求三棱锥的高.‎ ‎ 22.（本小题12分）‎ 已知直线l：，半径为4的圆C与直线l相切，圆心C在x轴上且在直线l的右上方.‎ ‎（Ⅰ）求圆C的方程；‎ ‎（Ⅱ）过点M (2，0)的直线与圆C交于A，B两点(A在x轴上方)，问在x轴正半轴上是否存在定点N，使得x轴平分∠ANB？若存在，请求出点N的坐标；若不存在，请说明理由.‎ ‎2019-2学期高二年级期末试题答案 数 学（文）‎ 一、选择题（本题共12小题，每小题5分，共60分，在每小题给出的四个选项中只有一个选项是符合题目要求的）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B D A C D A B D A C B A 二、填空题（本大题共4小题，每小题5分，共20分）‎ ‎13．2 14． 15． 16．‎ 三、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤. ‎ ‎17．（本小题10分）‎ 已知在等比数列 中，，且是和的等差中项．‎ ‎（Ⅰ）求数列的通项公式；‎ ‎（Ⅱ）若数列满足，求数列的前n项和．‎ 解：（Ⅰ）设公比为，则，，‎ ‎∵是和的等差中项，∴，，‎ 解得或（舍），∴． ..........................5分 ‎（Ⅱ），‎ 则．................10分 18． ‎（本小题12分）‎ 已知函数．‎ ‎（Ⅰ）求的最小正周期和单调递增区间；‎ ‎（Ⅱ）求在区间上的最大值及取得最大值时x的值．‎ 解：（Ⅰ）因为 ‎....................4分 故最小正周期为. ................................................................................5分 ‎ 由得 故的单调递增区间是． ................................ 8分 ‎（Ⅱ）因为，所以． ‎ 于是，当，即时，取得最大值............................12分 18． ‎（本小题12分）‎ 在中，角所对的边分别为，已知.‎ ‎（Ⅰ）求角；‎ ‎（Ⅱ）若点在边上，且，的面积为，求.‎ 解：（Ⅰ）由及正弦定理可得 ‎，故，‎ 而，所以，即. ...............................6分 ‎（Ⅱ）由及可得是正三角形.‎ 由的面积为可得，即，‎ 故，在中，由余弦定理可得，‎ 即. ..............................12分 18． ‎（本小题12分）‎ 某校高三课外兴趣小组为了解高三同学高考结束后是否打算观看2018年足球世界杯比赛的情况,从全校高三年级1500名男生、1000名女生中按分层抽样的方式抽取125名学生进行问卷调查,情况如下表:‎ 打算观看 不打算观看 女生 ‎20‎ m 男生 n ‎ ‎25‎ ‎（Ⅰ）求出表中数据m，n；‎ ‎（Ⅱ）判断是否有99%的把握认为观看2018年足球世界杯比赛与性别有关；‎ ‎（Ⅲ）为了计算“从10人中选出9人参加比赛”的情况有多少种，我们可以发现：它与“从10人中选出1人不参加比赛”的情况有多少种是一致的.现有问题：在打算观看2018年足球世界杯比赛的同学中有5名男生、2名女生来自高三（5）班，从中推选5人接受校园电视台采访，请根据上述方法，求被推选出的5人中恰有四名男生、一名女生的概率. ‎ 附： ‎ P(K2≥k0)‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.01‎ ‎0.005‎ K0 ‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ 解：（Ⅰ）根据分层抽样方法抽得女生50人，男生75人，所以m=50-20=30(人)，‎ ‎ n=75-25=50(人) ………………………………………………………………3分 ‎（Ⅱ）因为，所以有99%的把握认为观看2018年足球世界杯比赛与性别有关.………………………………………7分 ‎（Ⅲ）设5名男生分别为A、B、C、D、E，2名女生分别为a、b，由题意可知从7人中选出5人接受电视台采访，相当于从7人中挑选2人不接受采访，并且2‎ 人中恰有一男一女.而从7人中挑选2人的所有可能的结果为 ‎{A,B}{A,C}{A,D}{A,E}{A,a}{A,b}{B,C}{B,D}{B,E}{B,a}{B,b}{C,D}{C,E}{C,a} {C,b}{D,E}{D,a}{D,b}{E,a}{E,b}{a,b}，共21种，‎ 其中恰为一男一女的包括，‎ ‎{A,a}{A,b}{B,a}{B,b}{C,a}{C,b}{D,a}{D,b}{E,a}{E,b},共10种.‎ 因此所求概率为. ………………………………………12分 18． ‎（本小题12分）‎ 如图，在四棱锥中，底面为正方形，,. ‎ ‎（Ⅰ）若是的中点，求证：∥平面；‎ ‎（Ⅱ）若，，求点A到平面BED的距离.‎ 解：（Ⅰ）设交于,连接.‎ 在正方形中，为中点，则在三角形中,中位线 ∥,‎ 又平面,平面,‎ ‎∴∥平面. ............5分 ‎（Ⅱ）在中，设的中点为，连接，则，且∥‎ 又∵,，∴平面. ∴平面.‎ 又，∴, ‎ ‎∴ 三角形为直角三角形.‎ 又∵，（设三棱锥的高为h）‎ ‎∴，∴ ，‎ 解得. 所以点A到平面BED的距离为. ............12分 ‎ 19． ‎（本小题12分）‎ 已知直线l：，半径为4的圆C与直线l相切，圆心C在x轴上且在直线l的右上方.‎ ‎（Ⅰ）求圆C的方程；‎ ‎（Ⅱ）过点M (2，0)的直线与圆C交于A，B两点(A在x轴上方)，问在x轴正半轴上是否存在定点N，使得x轴平分∠ANB？若存在，请求出点N的坐标；若不存在，请说明理由.‎ 解：（Ⅰ）设圆心C(a，0) ()，‎ 则⇒a＝0或a＝ (舍).‎ 所以圆C的方程为x2＋y2＝16. .........................4分 ‎（Ⅱ）当直线AB⊥x轴时，x轴平分∠ANB.‎ 当直线AB的斜率存在时，设直线AB的方程为y＝k(x－2)，‎ 假设N(t，0) 符合题意，又设A(x1，y1)，B(x2，y2)，‎ 由得(k2＋1)x2－4k2x＋4k2－16＝0，‎ 所以x1＋x2＝，x1x2＝. .....................................................6分 若x轴平分∠ANB， 则kAN＝－kBN …………8分 即 ＋＝0⇒＋＝0‎ ‎⇒2x1x2－(t＋2)(x1＋x2)＋4t＝0‎ ‎⇒－＋4t＝0⇒t＝8. …………11分 所以存在点N为(8，0)时，能使得∠ANM＝∠BNM总成立. ……………12分