六年级下册数学试题-期中测试卷（A卷） 人教版（含解析）

六年级下册数学试题-期中测试卷（A卷） 人教版（含解析）

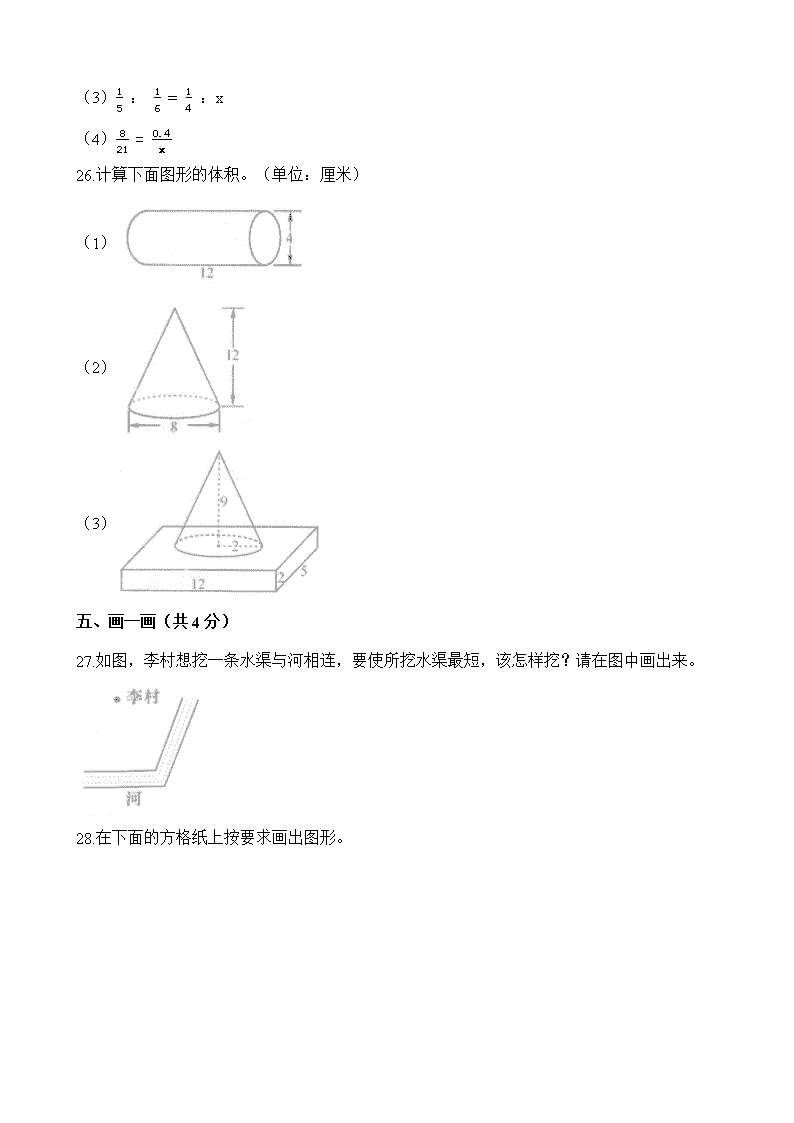
‎2020年人教版数学六年级下册期中测试卷（A卷）‎ 一、填一填（共24分）‎ ‎1.1.6：4=________：2.5= ‎12‎‎（）‎ ________=________%=________折=________成。 ‎ ‎2.在1~20中，最大质数是________，既是3的倍数又是5的倍数的数是________。 ‎ ‎3.如果向东直走60m到达A点记作+60m，那么向西直走30m到达B点记作________m，小强从B点直走到A点一共走了________m。 ‎ ‎4.如果 ‎3‎a‎=‎b‎6‎ ，那么a和b成________比例。比的后项一定，前项和比值成________比例。 ‎ ‎5.在一个比例里两个外项的积是最大的两位数，其中一个内项是3.3，另一个内项是________。 ‎ ‎6.把地面15千米的距离用3厘米的线段画在地图上，那么，这幅地图的比例尺是________；在比例尺为1：2000的地图上，6厘米的线段代表实际距离________米，实际距离180米在图上要画________厘米。 ‎ ‎7.一个圆锥和一个圆柱等底等高，它们的体积相差36立方分米，圆柱的体积是________立方分米，圆锥的体积是________立方分米． ‎ ‎8.把一个圆柱平均分成3段，变成了3个完全相等的圆柱，这时表面积比原来增加了50.24平方厘米，这个圆柱的底面积是________平方厘米。 ‎ ‎9.如图是________的表面展开图，它的高是________厘米，侧面积是________平方厘米，表面积是________平方厘米，体积是________立方厘米。 ‎ ‎10.口袋里放有足够多的红、白两种颜色的球，由若干个人轮流从袋中取球，每人取3个。若要保证有4人取出的球的颜色完全相同，至少应有________人取球。 ‎ 二、判一判（共6分）‎ ‎11.一件上衣进价120元按30%的利润定价销售，后打八五折促销仍可获利。（   ） ‎ ‎12.如果一个比例的两个内项乘积为1，那么它的两个外项一定互为倒数。（   ） ‎ ‎13.比例尺 ‎1000‎‎1‎ 表示的图上的距离大于实际距离。（   ） ‎ ‎14.圆柱的体积是圆锥的3倍，那么圆锥和圆柱肯定等底等高。（   ） ‎ ‎15.圆锥的高只有一条，就是顶点到底面圆心的距离。（   ） ‎ ‎16.把面积15cm2的长方形按3：1放大后，面积变为45cm2。（   ） ‎ 三、选一选（共8分）‎ ‎17.张华把2000元钱存入银行，整存整取5年，年利率是2.80%，到期时张华可得利息是（   ）元。 ‎ A. 224                                          B. 250                                          C. 280‎ ‎18.小明做20道数学题，做完的题数与没有做的题数（   ）。 ‎ A. 成正比例                                  B. 成反比例                                  C. 不成比例 ‎19.大、小两个圆柱的底面积之比是2：1，高之比是3：2，这两个圆柱的体积之比是（   ）。 ‎ A. 5：3                                         B. 6：3                                         C. 3：1‎ ‎20.一个圆锥的体积是47.1立方米，底面半径是3米，高是（   ）米。 ‎ A. 15                                            B. 5                                            C. ‎‎1‎‎2‎‎3‎ ‎21.将圆柱的侧面展开成一个平行四边形与展开成一个长方形比（   ）。 ‎ A. 面积小一些，周长大一些            B. 面积相等，周长大一些            C. 面积相等，周长小一些 ‎22.一幅零件图，图上距离4厘米表示实际距离4毫米，这幅图的比例尺是（   ）。 ‎ A. 1：1                                       B. 10：1                                       C. 1：10‎ ‎23.六（2）班进行队列训练，每行站8人，可以站6行。每行站12人，可以站几行？（   ）解答。 ‎ A. 能用正比例                               B. 能用反比例                               C. 不能用比例 ‎24.张阿姨给孩子买衣服，有红、黄、白三种颜色，但结果总是至少有两个孩子的颜色一样，她至少有（   ）个孩子。 ‎ A. 2                                           B. 3                                        C. 4                                           D. 6四、算一算（共24分）‎ ‎25.解比例。 ‎ ‎（1）12：x= ‎1‎‎2‎ ：0.3 ‎ ‎（2）‎1.4‎‎5‎‎=‎x‎8‎ ‎ ‎（3）‎1‎‎5‎ ： ‎1‎‎6‎ = ‎1‎‎4‎ ：x ‎ ‎（4）‎8‎‎21‎‎=‎‎0.4‎x ‎ ‎26.计算下面图形的体积。（单位：厘米） ‎ ‎（1）‎ ‎（2）‎ ‎（3）‎ 五、画一画（共4分）‎ ‎27.如图，李村想挖一条水渠与河相连，要使所挖水渠最短，该怎样挖？请在图中画出来。 ‎ ‎28.在下面的方格纸上按要求画出图形。 ‎ ‎（1）以直线L为对称轴画出图形A的对称图形B。 ‎ ‎（2）先将图形B向右平移4格，再以点O为中心逆时针旋转90°后得到图形C，画出图形C。 ‎ 六、解决问题（共34分）‎ ‎29.阳阳正在读一本科普书，第一周已经读了90页，比剩下的 ‎1‎‎3‎ 还多10页。还剩下多少页？（用方程解） ‎ ‎30.我买了6.5千克苹果花了16.25元，照这样计算，81.25元可以买到多少千克苹果？（用比例解） ‎ ‎31.如图是一幅地图的一部分，测得甲城到A地的距离是2cm，乙城到A地的距离是3.5cm。 ‎ ‎（1）如果甲城经过A地到乙城实际距离为110km，那么这幅地图的比例尺是多少？ ‎ ‎（2）如果王老师从乙城出发到达A地用了1小时，照这样的速度，王老师从A地到达甲城，还需要多少小时？ ‎ ‎（3）假如王老师的儿子同时从甲城出发开车来接她，按他的速度从甲城到乙城全程需要1.1小时可以到达，而王老师的搭车速度不变，那么，两人几小时后会在途中相遇？ ‎ ‎32.某工厂接到订单，要生产1000个不锈钢热水瓶（侧面为不锈钢板）（如图所示）。 ‎ ‎（1）一般需要多准备15%的材料作为损耗，那这个工厂一共需要准备多少平方米的不锈钢板？（接头处忽略不计） ‎ ‎（2）这款热水瓶的瓶盖是一个底面直径8cm、高5cm的圆柱。厂商准备在瓶盖的外面镀一层膜，如果不计损耗，一共需要多少平方米镀膜材料？ ‎ ‎33.六一儿童节，某图书网站所有童书都打六折。 ‎ ‎（1）徐颖买了《科学冒险漫画》和《鲁迪格来啦》各一套，一共要花多少钱？ ‎ ‎（2）一套打折后的《学生悦读文库》比原价便宜了多少钱？ ‎ ‎（3）这家网站还有“折后满299再减10%”的活动，上面3套书徐颖各买一套的话能不能参加这个活动？如果能参加，她一共要花多少钱？ ‎ 七、挑战题（附加10分）‎ ‎34.东东和明明去看电影，一张电影票的价钱是东东所有钱的 ‎6‎‎25‎ ，是明明所有钱的 ‎3‎‎5‎ 。两人各自买了一张电影票后，东东剩下的钱比明明剩下的钱多30元。明明买电影票前有多少元？ ‎ 答案解析部分 一、填一填（共24分）‎ ‎1.【答案】 1；30；40；四；四 ‎ ‎【考点】百分数的应用--折扣，百分数的应用--成数，比与分数、除法的关系，比的基本性质，比的化简与求值 ‎ ‎【解析】【解答】解：1.6：4=1：2.5= ‎12‎‎30‎=40%=四折=四成。 故答案为：1；30；40；四；四。 【分析】比值=比的前项÷比的后项； 比的基本性质：比的前项和后项同时乘或除以相同的数（0除外），比值不变； 小数化百分数，先把小数的小数点向右移动两位，再在后面加上百分号； 百分之几十就是几折，也是几成。‎ ‎2.【答案】 19；15 ‎ ‎【考点】2、5的倍数的特征，3的倍数的特征，合数与质数的特征 ‎ ‎【解析】【解答】解：在1~20中，最大质数是19，既是3的倍数又是5的倍数的数是15。 故答案为：19；15。 【分析】质数是指这个数除了1和它本身外没有其他因数的数； 3的倍数的数字特征：这个数的各个数位上的数字之和是3的倍数； 5的倍数的数字特征：这个数的末尾是0或5。‎ ‎3.【答案】 -30；90 ‎ ‎【考点】正、负数的意义与应用 ‎ ‎【解析】【解答】解：向西直走30m到达B点记作-30m，小强从B点直走到A点一共走了60+30=90m。 故答案为：-30；90。 【分析】用正负数可以表示具有相反意义的量，向东记为正，那么向西记为负； 小强从B点直走到A点一共走的距离=起点到A的距离+起点到B的距离。‎ ‎4.【答案】 反；正 ‎ ‎【考点】成正比例的量及其意义，成反比例的量及其意义 ‎ ‎【解析】【解答】解：如果‎3‎a‎=‎b‎6‎ ， 那么ab=18，所以a和b成反比例；比的后项=比的前项÷比值，所以比的后项一定，前项和比值成正比例。 故答案为：反；正。 ‎ ‎ 【分析】若xy=k（k是常数，x，y≠0），那么x和y成反比例； 若yx=k（k是常数，x，y≠0），那么x和y成正比例。‎ ‎5.【答案】 30 ‎ ‎【考点】比例的基本性质 ‎ ‎【解析】【解答】解：99÷3.3=30，所以另一个内项是30。 故答案为：30。 【分析】最大的两位数是99； 比例的基本性质：两个外项的积等于两个内项的积，所以另一个内项=两个外项的积÷其中一个内项。‎ ‎6.【答案】 1：500000；120；9 ‎ ‎【考点】比例尺的认识，应用比例尺求图上距离或实际距离 ‎ ‎【解析】【解答】解：15千米=1500000厘米，3：1500000=1：500000，所以这幅地图的比例尺是1：500000；在比例尺为1：2000的地图上，6厘米的线段代表实际距离6÷‎1‎‎2000‎=12000厘米=120米，实际距离180米在图上要画180×100×‎1‎‎2000‎=9厘米。 故答案为：1：500000；120；9。 【分析】在有关比例尺的计算中，图上距离和实际距离的单位要统一； 比例尺=图上距离：实际距离；实际距离=图上距离÷比例尺；图上距离=实际距离×比例尺。‎ ‎7.【答案】 54；18 ‎ ‎【考点】圆柱与圆锥体积的关系 ‎ ‎【解析】【解答】解：圆锥的体积=36÷2=18立方分米，圆柱的体积=18+36=54立方分米。 故答案为：54；18。 【分析】圆柱的体积是与它等底等高圆锥体积的3倍，所以它们的体积之差是2个圆锥的体积，据此可以求出圆锥的体积，然后用体积差加上圆锥的体积就是圆柱的体积。‎ ‎8.【答案】 12.56 ‎ ‎【考点】圆的面积 ‎ ‎【解析】【解答】解：50.24÷4=12.56平方厘米，所以这个圆柱的底面积是12.56平方厘米。 故答案为：12.56。 【分析】将把一个圆柱平均分成3段，求就是分2次，每分一次就会多出两个圆柱的底面，所以这个圆柱的底面积=增加的表面积÷4。‎ ‎9.【答案】 圆柱；3；18.84；25.12；9.42 ‎ ‎【考点】圆柱的特征，圆柱的侧面积、表面积，圆柱的体积（容积） ‎ ‎【解析】【解答】解：图中的图形是圆柱的表面展开图，它的高是3厘米，侧面积是6.28×3=18.84平方厘米，6.28÷3.14÷2=1厘米，12×3.14×2+18.84=25.12平方厘米，所以表面积是25.12平方厘米，12×3.14×3=9.42立方厘米，所以体积是9.42立方厘米。 故答案为：圆柱；3；18.84；25.12；9.42。 【分析】圆柱的底面半径=圆柱的底面周长÷π÷2；圆柱的侧面积=圆柱的底面周长×圆柱的高；圆柱的表面积=πr2×2+圆柱的侧面积；圆柱的体积=πr2h。‎ ‎10.【答案】 13 ‎ ‎【考点】抽屉原理 ‎ ‎【解析】【解答】解：4×3+1=13，所以至少应有13人取球。 故答案为：13。 【分析】3个球的颜色的种类：红红红、红红白、红白白、白白白，一共有4种，因为要保证有4人取出的球的颜色完全相同，考虑最不利的情况，即每种颜色都有3人取，那么再加上一个人就是至少有的人数。‎ 二、判一判（共6分）‎ ‎11.【答案】 正确 ‎ ‎【考点】百分数的应用--折扣，百分数的应用--利润 ‎ ‎【解析】【解答】解：120×（1+30%）=156元，156×85%=132.6元>120元，所以最后可获利。 故答案为：正确。 【分析】这件衣服的售价=进价×（1+利润率），打折后的价钱=这件衣服的售价×折扣数，然后与衣服的进价进行比较，如果比进价多，那么就获利了，如果比进价少，那么就没有获利。‎ ‎12.【答案】 正确 ‎ ‎【考点】倒数的认识，比例的基本性质 ‎ ‎【解析】【解答】解：如果一个比例的两个内项乘积为1，那么它的两个外项一定互为倒数。 故答案为：正确。 【分析】在比例中，两个内项的积等于两个外项的积，而乘积为1的两个数互为倒数。‎ ‎13.【答案】 正确 ‎ ‎【考点】比例尺的认识 ‎ ‎【解析】【解答】解：比例尺‎1000‎‎1‎表示的图上的距离大于实际距离。 故答案为：正确。 【分析】比例尺=比的前项÷比的后项，比的前项比后项大，那么图上的距离大于实际距离。‎ ‎14.【答案】 错误 ‎ ‎【考点】圆柱的体积（容积），圆锥的体积（容积），圆柱与圆锥体积的关系 ‎ ‎【解析】【解答】解：圆柱的体积是圆锥的3倍，那么圆锥和圆柱不一定等底等高。 故答案为：错误。 【分析】例如：底面积是3，高是5的圆柱，它的体积是15；底面积是9，高是5的圆锥，它的体积也是15，但是它们不是等底等高。‎ ‎15.【答案】 正确 ‎ ‎【考点】圆锥的特征 ‎ ‎【解析】【解答】解：圆锥的高只有一条，就是顶点到底面圆心的距离。 故答案为：正确。 【分析】根据圆锥的高的特征作答即可。‎ ‎16.【答案】 错误 ‎ ‎【考点】比的应用 ‎ ‎【解析】【解答】解：把面积15cm2的长方形按3：1放大后，面积变为15×3×3=135cm2。 故答案为：错误。 【分析】长方形的面积=长×宽，所以把面积15cm2的长方形按3：1放大后，现在长方形的面积=（长×3）×（宽×3）=长×宽×9=原来长方形的面积×9。‎ 三、选一选（共8分）‎ ‎17.【答案】 C ‎ ‎【考点】百分数的应用--利率 ‎ ‎【解析】【解答】解：2000×2.80%×5=280元，所以到期时张华可得利息是280元。 故答案为：C。 【分析】到期时张华可以获得利息的钱数=张华存的钱数×年利率×存的年份，据此作答即可。‎ ‎18.【答案】 C ‎ ‎【考点】成正比例的量及其意义，成反比例的量及其意义 ‎ ‎【解析】【解答】解：小明做20道数学题，做完的题数与没有做的题数不成比例。 故答案为：C。 【分析】做完的题数+没有做的题数=一共做的题数，所以它们之间不成比例。‎ ‎19.【答案】 C ‎ ‎【考点】圆柱的体积（容积），比的应用 ‎ ‎【解析】【解答】解：（2×3）：（1×2）=6：2=3：1，所以这两个圆柱的体积之比是3：1。 故答案为：C。 【分析】大圆柱的体积：小圆柱的体积=（大圆柱的底面积占的份数×大圆柱的高占的份数）：（小圆柱的底面积占的份数×小圆柱的高占的份数），据此作答即可。‎ ‎20.【答案】 B ‎ ‎【考点】圆锥的体积（容积） ‎ ‎【解析】【解答】解：47.1÷‎1‎‎3‎÷3.14÷32=5米，所以高是5米。 故答案为：B。 【分析】圆锥的高=圆锥的体积÷‎1‎‎3‎÷π÷r2 ， 据此作答即可。‎ ‎21.【答案】 B ‎ ‎【考点】圆柱的侧面积、表面积 ‎ ‎【解析】【解答】解：将圆柱的侧面展开成一个平行四边形与展开成一个长方形比，面积相等，周长大一些。 故答案为：B。 【分析】将圆柱的侧面展开成一个平行四边形与展开成一个长方形，这是这个平行四边形和长方形都是圆柱的侧面积，所以面积相等；平行四边形的底和长方形的长都是圆柱的底面周长，长方形的宽是圆柱的高，而平行四边形的腰比圆柱的高长，所以周长大一些。‎ ‎22.【答案】 B ‎ ‎【考点】比例尺的认识 ‎ ‎【解析】【解答】解：4厘米=40毫米，40：4=10：1，所以这幅图的比例尺是10：1。 故答案为：B。 【分析】先把单位进行换算，即4厘米=40毫米，那么比例尺=图上距离：实际距离。‎ ‎23.【答案】 B ‎ ‎【考点】反比例应用题 ‎ ‎【解析】【解答】解：每行站的人数×站的行数=总人数，所以可以利用反比例作答。 故答案为：B。 【分析】总人数一定，每行站的人数和站的行数成反比，据此作答即可。‎ ‎24.【答案】 C ‎ ‎【考点】抽屉原理 ‎ ‎【解析】【解答】解：3+1=4，所以她至少有4个孩子。 故答案为：C。 【分析】考虑最不利的情况，先让孩子把这三种颜色的衣服各穿一件，那么再加上一个孩子，就有两个孩子的颜色一样。‎ 四、算一算（共24分）‎ ‎25.【答案】 （1）   12：x=‎1‎‎2‎：0.3 解：‎1‎‎2‎x=3.6  ‎1‎‎2‎x÷‎1‎‎2‎=3.6÷‎1‎‎2‎          x=7.2 （2）   ‎1.4‎‎5‎‎=‎x‎8‎ 解：5x=11.2   5x÷5=11.2÷5         x=2.24 （3）  ‎1‎‎5‎：‎1‎‎6‎=‎1‎‎4‎：x 解：‎1‎‎5‎x=‎1‎‎24‎   ‎1‎‎5‎x÷‎1‎‎5‎=‎1‎‎24‎÷‎1‎‎5‎          x=‎5‎‎24‎ （4）    ‎8‎‎21‎‎=‎‎0.4‎x 解：8x=8.4   8x÷8=24÷8         x=1.05 ‎ ‎【考点】应用比例的基本性质解比例 ‎ ‎【解析】【分析】解比例时，可以利用比例的基本性质，即两个外项的积等于两个内项的积，把含有x的项放在等号的左边，把常数项放在等号的右边，然后等号两边同时除以x前面的系数，就可以得到x的值。‎ ‎26.【答案】 （1）解：12×（4÷2）2×3.14 =12×4×3.14 =48×3.14 =150.72（立方厘来） （2）解：‎1‎‎3‎×12×（8÷2）2×3.14 =4×50.24 =200.96（立方厘米） （3）解：12×2×5+‎1‎‎3‎×22×3.14×9 =120+4×3.14×3 =157.68（立方厘米） [来源:学§科§网]‎ ‎【考点】长方体的体积，圆柱的体积（容积），圆锥的体积（容积） ‎ ‎【解析】【分析】圆柱的体积=（底面直径÷2）2×π×h；圆锥的体积=‎1‎‎3‎×（底面直径÷2）2×π×h；长方体的体积=长×宽。据此作答即可。‎ 五、画一画（共4分）‎ ‎27.【答案】 ‎ ‎【考点】点到直线的距离及应用 ‎ ‎【解析】【分析】点到直线的距离，垂线段最短，据此作答即可。‎ ‎28.【答案】 （1） （2）‎ ‎【考点】将简单图形平移或旋转一定的度数，补全轴对称图形 ‎ ‎【解析】【分析】做一个图形的轴对称图形时，先过这个图形的关键点做对称轴的垂线，然后数出这个点到对称轴的距离，并在对称轴的另一边的相同距离的位置做上标记，把这些标记连接起来即可； 把一个图形平移，先把这个图形的关键点平移，然后把这些关键点连接起来即可； 把一个图形绕其上面一点逆时针旋转一定的度数，先把这个点连接的边逆时针旋转相同的度数，最后把剩下的边连接起来即可。‎ 六、解决问题（共34分）‎ ‎29.【答案】 解： 设还剩下x页。 ‎1‎‎3‎x+10=90 ‎ ‎       ‎1‎‎3‎x=80          x=240 答：还剩下240页。 ‎ ‎【考点】列方程解含有一个未知数的应用题 ‎ ‎【解析】【分析】本题可以设还剩下x页，题中存在的等量关系是：剩下的页数×已经读的页数是剩下的几分之几+还多的页数=第一周已经读的页数，据此代入数据和字母作答即可。‎ ‎30.【答案】 解： 解：设可以买到x千克苹果。 6.5：16.25=x：81.25       16.25x=528.125                x=32.5 答：可以买到32.5千克苹果。 ‎ ‎【考点】应用比例解决实际问题 ‎ ‎【解析】【分析】本题可以设可以买到x千克苹果，题中存在的比例关系是：6.5：买6.5千克的苹果花的钱数=花81.25元可以买到苹果的千克数：81.25，据此代入数据和字母作答即可。‎ ‎31.【答案】 （1）解：110km=11000000cm， ‎3.5+2‎‎11000000‎ = ‎1‎‎2000000‎ ，比例尺为1：2000000 ‎ 答：这幅地图的比例尺是1：2000000。‎ ‎ （2）解：甲城到A地的距离：2×2000000=4000000（厘米）=40（千米） [来源:Z*xx*k.Com]‎ A地到乙城的距离：3.5×2000000=7000000（厘米）=70（千米）‎ ‎40÷（ ‎70‎‎1‎ ）= ‎4‎‎7‎ （小时）‎ 答：还需要 ‎4‎‎7‎ 小时。‎ ‎ （3）解： ‎40+70‎‎1.1‎ =100（千来/时） ‎ ‎40+70‎‎100+70‎‎ = ‎11‎‎17‎ （小时）‎ 答：两人 ‎11‎‎17‎ 小时后会在途中相遇。‎ ‎【考点】相遇问题，应用比例尺求图上距离或实际距离 ‎ ‎【解析】【分析】（1）先把单位进行换算，即110km=11000000cm，比例尺=图上距离：实际距离； （2）实际距离=图上距离÷比例尺，据此先算出甲城到A地的距离和A地到乙城的距离，那么王老师的速度=甲城到A地的距离÷王老师从甲城到A地用的时间，那么王老师从A地到达甲城还需要的时间=A地到乙城的距离÷那么王老师的速度； （3）王老师儿子的速度=（甲城到A地的距离+A地到乙城的距离）÷从甲城到乙城全程需要的时间，所以两人相遇用的时间=（甲城到A地的距离+A地到乙城的距离）÷两人的速度和。‎ ‎32.【答案】 （1）解：3.14×15×40×1000 =47.1×40×1000 =1884×1000 =1884000（cm2） =188.4（m2） 188.4×（15%+1）=216.66（m2） 答：这个工厂一共需要准备216.66平方米的不锈钢板。 （2）解： 3.14×8×5+3.14×（8÷2）2 =125.6+50.24 =175.84（cm2） 1000×175.84=175840（cm2）=17.584（m2） 答：一共需要17.584平方米镀膜材料。 ‎ ‎【考点】圆柱的侧面积、表面积 ‎ ‎【解析】【分析】（1）1000个不锈钢热水瓶需要钢板的面积=π×底面直径×侧面的高×1000，然后进行单位换算，即1平方米=10000平方厘米，所以这个工厂一共需要准备不锈钢板的平方米数=1000个不锈钢热水瓶需要钢板的面积×（1+多准备百分之几的材料）； （2）每个热水瓶的瓶盖需要镀膜材料的面积=（底面直径÷2）2×π+底面直径×π×瓶盖的高，然后进行单位换算，即1平方米=10000平方厘米，所以一共需要镀膜材料的平方米数=每个热水瓶的瓶盖需要镀膜材料的面积×1000。‎ ‎33.【答案】 （1）解：100×60%+390×60%=294（元） ‎ 答：一共要花294元钱。‎ ‎ （2）解：238×（1-60%）=95.2（元） ‎ 答：比原价便宜了95.2元钱。‎ ‎ （3）解：（100+238+390）×60%=436.8（元） 436.8>299，能 ‎ ‎436.8×（1-10%）=393.12（元）‎ 答：能参加这个活动，她一共要花393.12元钱。‎ ‎【考点】百分数的应用--增加或减少百分之几，百分数的应用--折扣 ‎ ‎【解析】【分析】几折就是百分之几十，所以六折就是60%。 （1）一共要花的钱数=一套《科学冒险漫画》的价钱×打的折扣数+一套《鲁迪格来啦》的价钱×打的折扣数，据此代入数据作答即可； （2）一套打折后的《学生悦读文库》比原价便宜的钱数=一套《学生悦读文库》的价钱×（1-打的折扣数）； （3）这3套书各买一套需要花的钱数=三种书的价钱之和×打的折扣数，然后与299进行比较，经过计算比299大，所以能参加活动，所以一共要花的钱数=这3套书各买一套需要花的钱数×（1-减少百分之几）。‎ 七、挑战题（附加10分）‎ ‎34.【答案】 解：东东与明明买电影票前的钱数比是 ‎3‎‎5‎ ： ‎6‎‎25‎ =5：2 30÷ ‎5−2‎‎2‎ =20（元） ‎ 答：明明买电影票前有20元。‎ ‎【考点】比的应用 ‎ ‎【解析】【分析】电影票的价钱是不变的，所以东东与明明买电影票前的钱数比=这张电影票的价钱是明明所有钱的几分之几：这张电影票的价钱是东东所有钱的几分之几，所以明明买电影票前有的钱数=东东剩下的钱比明明剩下的钱多的钱数÷东东与明明买电影票前的钱数的份数之差明明买电影票前的钱数占的份数。‎