2020九年级数学上册第2章一元二次方程2

2020九年级数学上册第2章一元二次方程2

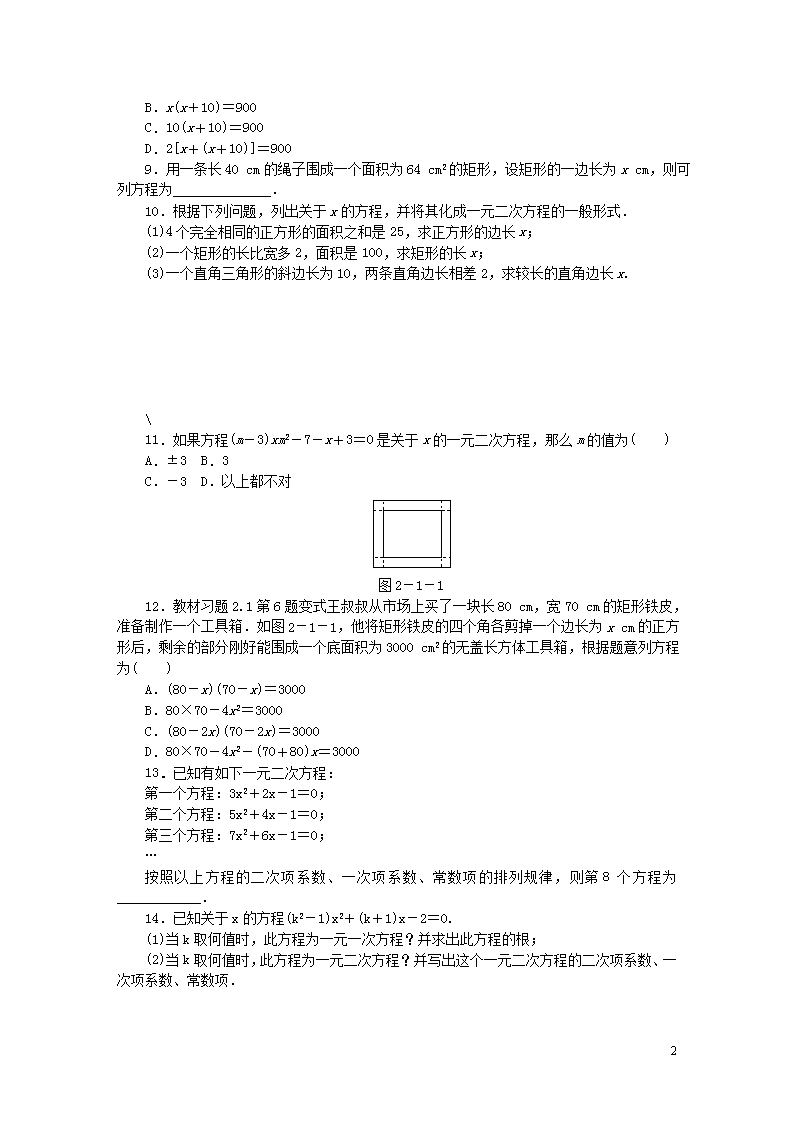
‎2.1　一元二次方程 知识点 1　一元二次方程的概念及一般形式 ‎1．将一元二次方程x2－3＝－3x化为一般形式为__________，其中，二次项系数是________，一次项系数是________，常数项是________．‎ ‎2．下列选项中一定是关于x的一元二次方程的是(　　)‎ A．x2＋＝0‎ B．ax2＋bx＋c＝0‎ C．x2＝1‎ D．(x＋1)(x－1)－x2＋1＝0‎ ‎3．已知一元二次方程x2－4＝0，则下列关于它的说法正确的是(　　)‎ A．不是一般形式 B．一次项系数是0‎ C．常数项是4 D．没有二次项系数 ‎4．当a满足条件：________时，关于x的方程(‎2a－1)x2＋3x－1＝0是一元二次方程．‎ ‎5．写出一个关于x的一元二次方程，使它的二次项系数、一次项系数、常数项分别为1，2，－1，该方程是______________．‎ ‎6．把下列方程化成关于x的一元二次方程的一般形式，并写出它们的二次项系数、一次项系数及常数项．‎ ‎(1)3x(x－8)＝1；‎ ‎(2)(x＋m)(2x－‎5m)－‎12m2‎＝0(m为常数)．‎ 知识点 2　依据实际问题建立一元二次方程模型 ‎7．2017·黔南州“一带一路”国际合作高峰论坛于‎2017年5月14日至15日在北京举行，在论坛召开之际，福田欧辉陆续向缅甸仰光公交公司交付1000辆清洁能源公交车，以2017客车海外出口第一大单的成绩，创下了客车行业出口之最，同时，这也是在国家“一带一路”倡议下，福田欧辉代表“中国制造”走出去的成果．预计到2019年，福田公司将向海外出口清洁能源公交车达到3000辆．设平均每年的出口增长率为x，则可列方程为(　　)‎ A．1000(1＋x%)2＝3000‎ B．1000(1－x%)2＝3000‎ C．1000(1＋x)2＝3000‎ D．1000(1－x)2＝3000‎ ‎8．绿苑小区在规划设计时，准备在两幢楼房之间设置一块面积为900平方米的矩形绿地，并且长比宽多‎10米．设绿地的宽为x米，根据题意，可列方程为(　　)‎ A．x(x－10)＝900 ‎ 5‎ B．x(x＋10)＝900‎ C．10(x＋10)＝900 ‎ D．2[x＋(x＋10)]＝900‎ ‎9．用一条长‎40 cm的绳子围成一个面积为‎64 cm2的矩形，设矩形的一边长为x cm，则可列方程为______________．‎ ‎10．根据下列问题，列出关于x的方程，并将其化成一元二次方程的一般形式．‎ ‎(1)4个完全相同的正方形的面积之和是25，求正方形的边长x；‎ ‎(2)一个矩形的长比宽多2，面积是100，求矩形的长x；‎ ‎(3)一个直角三角形的斜边长为10，两条直角边长相差2，求较长的直角边长x.‎ ‎‎ ‎11．如果方程(m－3)xm2－7－x＋3＝0是关于x的一元二次方程，那么m的值为(　　)‎ A．±3 B．3‎ C．－3 D．以上都不对 图2－1－1‎ ‎12．教材习题2.1第6题变式王叔叔从市场上买了一块长‎80 cm，宽‎70 cm的矩形铁皮，准备制作一个工具箱．如图2－1－1，他将矩形铁皮的四个角各剪掉一个边长为x cm的正方形后，剩余的部分刚好能围成一个底面积为‎3000 cm2的无盖长方体工具箱，根据题意列方程为(　　)‎ A．(80－x)(70－x)＝3000‎ B．80×70－4x2＝3000‎ C．(80－2x)(70－2x)＝3000‎ D．80×70－4x2－(70＋80)x＝3000‎ ‎13．已知有如下一元二次方程：‎ 第一个方程：3x2＋2x－1＝0；‎ 第二个方程：5x2＋4x－1＝0；‎ 第三个方程：7x2＋6x－1＝0；‎ ‎…‎ 按照以上方程的二次项系数、一次项系数、常数项的排列规律，则第8个方程为____________．‎ ‎14．已知关于x的方程(k2－1)x2＋(k＋1)x－2＝0.‎ ‎(1)当k取何值时，此方程为一元一次方程？并求出此方程的根；‎ ‎(2)当k取何值时，此方程为一元二次方程？并写出这个一元二次方程的二次项系数、一次项系数、常数项．‎ 5‎ ‎15．如图2－1－2，在宽为‎20 m，长为‎30 m的矩形场地上，修筑同样宽的两条道路，余下的部分作为耕地，且使耕地的面积为‎500 m2‎.若设路宽为x m，根据题意列出方程，并将其化成一元二次方程的一般形式．‎ 图2－1－2‎ ‎16．教材或资料中会出现这样的题目：把方程x2－x＝2化为一元二次方程的一般形式，并写出它的二次项系数、一次项系数和常数项．‎ 现把上面的题目改编为下面的两个小题，请解答．‎ ‎(1)下列式子中，有哪几个是方程x2－x＝2所化的一元二次方程的一般形式？________(答案只写序号)．‎ ‎①x2－x－2＝0；②－x2＋x＋2＝0；‎ ‎③x2－2x＝4；④－x2＋2x＋4＝0；‎ ‎⑤x2－2 x2－4 ＝0.‎ ‎(2)方程x2－x＝2化为一元二次方程的一般形式后，它的二次项系数、一次项系数、常数项之间的比固定吗？如果固定，这个比是多少？‎ ‎ ‎ ‎17．如图2－1－3所示，在△ABC中，∠B＝90°，点P从点A开始沿AB边向点B以厘米/秒的速度移动，点Q从点B开始沿BC边向点C以2厘米/秒的速度移动．点P，Q分别从A，B两点同时出发，经过几秒△PBQ的面积等于6平方厘米？(只列出方程即可)‎ 5‎ 图2－1－3‎ ‎　　　　‎ ‎ ‎ 5‎ ‎1．x2＋3x－3＝0　1　3　－3‎ ‎2．C　[解析] 选项A是分式方程，选项B中未强调a≠0，选项D化简整理后不含x的二次项，故它们都不是一元二次方程．选项C符合一元二次方程的定义，故选C.‎ ‎3． B ‎4．a≠　5.x2＋2x－1＝0‎ ‎6．解：(1)一般形式：3x2－24x－1＝0.‎ 二次项系数为3，一次项系数为－24，常数项为－1.‎ ‎(2)一般形式：2x2－3mx－‎17m2‎＝0.‎ 二次项系数为2，一次项系数为－3m，常数项为－17m2.‎ ‎7．C　[解析] 根据题意得出2018年福田公司向海外出口清洁能源公交车1000(1＋x)辆，2019年为1000(1＋x)2辆，则1000(1＋x)2＝3000.故选C.‎ ‎8． B ‎9．x(20－x)＝64　[解析] ∵设矩形的一条边长为x cm，由矩形的周长为‎40 cm，可得矩形的另一条边长为(20－x)cm，根据矩形的面积是相邻两边长的积，可列出方程为x(20－x)＝64.‎ ‎10．解：(1)依题意得4x2＝25，化为一元二次方程的一般形式，得4x2－25＝0.‎ ‎(2)依题意得x(x－2)＝100，化为一元二次方程的一般形式，得x2－2x－100＝0.‎ ‎(3)依题意得x2＋(x－2)2＝102，化为一元二次方程的一般形式，得2x2－4x－96＝0.‎ ‎11．C　[解析] 依题意，有m2－7＝2且m－3≠0，解得m＝－3.‎ ‎12．C　[解析] 根据题意可知裁剪后的底面的长为(80－2x)cm，宽为(70－2x)cm，从而有(80－2x)(70－2x)＝3000.‎ ‎13．17x2＋16x－1＝0　[解析] 二次项系数是从3开始的连续奇数，一次项系数是从2开始的连续偶数，常数项都是－1，所以第8个方程为17x2＋16x－1＝0.‎ ‎14．解：(1)若原方程为关于x的一元一次方程，则应满足解得k＝1.‎ 所以当k＝1时，此方程为关于x的一元一次方程，方程为2x－2＝0，解得x＝1.‎ ‎(2)若原方程为关于x的一元二次方程，则应满足k2－1≠0，即k≠±1.所以当k≠±1时，此方程为关于x的一元二次方程，它的二次项系数为k2－1，一次项系数为k＋1，常数项为－2.‎ ‎15．解：通过平移，可将各部分耕地拼凑成一个矩形区域，则该矩形区域的长应为(30－x)m，宽应为(20－x)m，‎ 根据矩形面积公式可得(30－x)(20－x)＝500，‎ 整理得x2－50x＋100＝0.‎ ‎16．解：(1)①②④⑤‎ ‎(2)固定．二次项系数、一次项系数、常数项之间的比为－1∶2∶4.‎ ‎17．解：设经过x秒△PBQ的面积等于6平方厘米，则PB＝(6－x)厘米，BQ＝2x厘米，于是S△PBQ＝BP·BQ，所以可列方程为(6－x)·2x＝6.‎ 5‎